线性代数-矩阵-【2】矩阵生成 C和C++实现

矩阵的知识点之多足以写成一本线性代数。

所以我们把矩阵的运算封装成矩阵类。以C++为主进行详解。

点击这里可以跳转至

【1】矩阵汇总：http://www.cnblogs.com/HongYi-Liang/p/7287369.html

【2】矩阵生成：现在的位置

【3】矩阵加减：http://www.cnblogs.com/HongYi-Liang/p/7287403.html

【4】矩阵点乘：http://www.cnblogs.com/HongYi-Liang/p/7287324.html

【5】矩阵化简：http://www.cnblogs.com/HongYi-Liang/p/7464850.html

......

---

C++语言：

作为矩阵的第一遍程序详解，讲述的如何生成矩阵，以下列矩阵为例子详解

分段详解：

基本成员：

矩阵类的成员变量有三个：

1. 矩阵的行数
2. 矩阵的列数
3. 用二维向量（数组）存放矩阵中的所有元素

    int m_iRows;
    int m_iColumns;
    vector<vector<T>>  m_vecMatrix;

接下来，为了生成矩阵，这里提供两种生成矩阵的方法。

• 生成一个空的矩阵，把数据一行一行或者一列一列地把数据加入矩阵中。
• 生成一个n行m列，且元素全为0的矩阵。一个一个地改变矩阵内部的元素。

方法一

包括以下两个成员函数

1. 加入一行
2. 加入一列

（成员函数请展开）

bool addOneRowToBack(vector<T> &vec);            //往最底插入一行
bool addOneColumToBack(vector<T> &vec);          //往最后插入一列

加入一行：

template <typename T>
bool Matrix<T>::addOneRowToBack(vector<T> &vec)
{
    /*Matrix has had datas*/
    if(m_iColumns !=)
    {
        if(vec.size() != m_iColumns)//input data columns not equal matrix columns
        {
            cout<<"addOneRowToBack(): columns not equal"<<endl;
            return false ;
        }
    }

    /*Adding vec to m_vecDatas*/
    m_vecMatrix.push_back(vec);
    m_iRows ++;
    m_iColumns = vec.size();
    return true;
}

加入一列：

template <typename T>
bool Matrix<T>::addOneColumToBack(vector<T> &vec)
{
    /*Matrix has had datas*/
    if(m_iRows !=)
    {
        if(vec.size() != m_iRows)//input data columns not equal matrix columns
        {
            cout<<"addOneColumsToBack(): rows not equal"<<endl;
            return false ;
        }
    }
    else
    {
        vector<T> tempVec;
        m_iRows = vec.size();
        for(int i=;i<m_iRows;i++)
        {
            m_vecMatrix.push_back(tempVec);
        }
    }

    /*Adding vec to m_vecDatas*/
    for(int i=;i<m_iRows;i++)
    {
        m_vecMatrix[i].push_back(vec[i]);
    }
    m_iColumns ++;
    m_iRows = vec.size();
    return true;
}

我们可以通过调用添加行和添加列给矩阵增加行/列，下面我们通过addOneRowToBack（）方法添加一行，得到一个1行3列，值为| 1 2 3 |的矩阵

    vector<int> vector1;
    for(int i=;i<=;i++)
    {
        vector1.push_back(i);
    }
    Matrix<int> matrix;
    matrix.addOneRowToBack(vector1);         

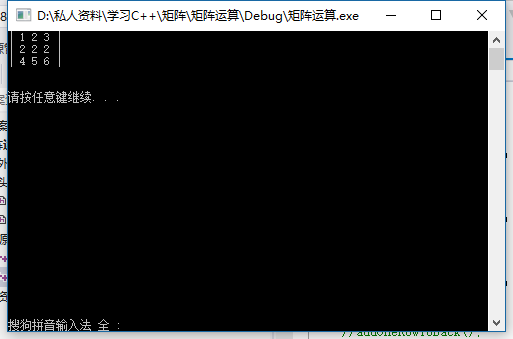
同样，我们可以连续使用addOneRowToBack（）函数来添加3行，让其成为一个3行3列的矩阵

    vector<int> vector1;
    vector<int> vector2;
    vector<int> vector3;
    for(int i=;i<=;i++)
    {
        vector1.push_back(i);
    }
    for(int i=;i<=;i++)
    {
        vector2.push_back();
    }
    for(int i=;i<=;i++)
    {
        vector3.push_back(i);
    }
    Matrix<int> matrix;
    matrix.addOneRowToBack(vector1);
    matrix.addOneRowToBack(vector2);
    matrix.addOneRowToBack(vector3);
    matrix.printfAll();

可以得到如下结果：

方法二

包含以下成员函数

1. 构造函数重载：构造一个n行m列的全0矩阵
2. 改变第n行第m个元素的值

Matrix(int rows,int columns);
bool setSpecifiedElem(int row,int column,T value);

构造函数重载：

template <typename T>
Matrix<T>::Matrix(int rows,int columns)
{
    vector<T> tempVec;    

    m_iRows = ;
    m_iColumns =;
    m_vecMatrix.clear();

    //reduce a vector for adding
    for(int i=;i<columns;i++)
    {
        tempVec.push_back();
    }

    //puduce a zero matirx
    for(int i=;i<rows;i++)
    {
        addOneRowToBack(tempVec);
    }
}

改变第n行第m个元素（从0开始）：

template <typename T>
bool Matrix<T>::setSpecifiedElem(int row,int column,T value)    //设置第row行第column个元素的值为value
{
    if(row > m_iRows- ||column > m_iColumns-)
    {
        return false;
    }    

    m_vecMatrix[row][column]=value;
    return true;
}

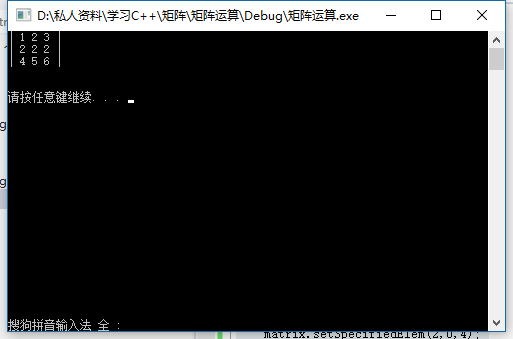
调用方法：

    Matrix<double> matrix(,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.printfAll();

运行结果：

---

C语言

以后补充