优先级队列Priority_queue
定义
拥有权值观点的queue,,一个是返回最高优先级对象,一个是在底端添加新的对象。这种数据结构就是优先级队列(Priority Queue) 。
实现
利用max_heap完成,以vector表现的完全二叉堆。max_heap可以满足priority_heap所需要的依照权值高低自动递减的特性。
二叉堆
二叉堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。 有了这一性质,那么二叉堆上最大值就是根节点了。
二叉堆的表现形式:我们可以使用数组的索引来表示元素在二叉堆中的位置。
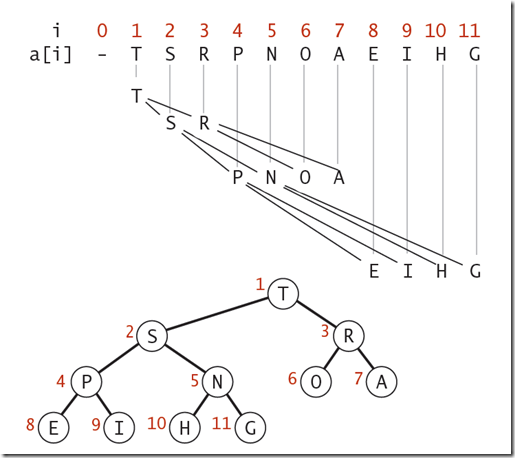
从二叉堆中,我们可以得出:
· 元素k的父节点所在的位置为[k/2]
· 元素k的子节点所在的位置为2k和2k+1
跟据以上规则,我们可以使用二维数组的索引来表示二叉堆。通过二叉堆,我们可以实现插入和删除最大值都达到O(nlogn)的时间复杂度。
对于堆来说,最大元素已经位于根节点,那么删除操作就是移除并返回根节点元素,这时候二叉堆就需要重新排列;当插入新的元素的时候,也需要重新排列二叉堆以满足二叉堆的定义。现在就来看这两种操作。
从下至上的重新建堆操作: 如果一个节点的值大于其父节点的值,那么该节点就需要上移,一直到满足该节点大于其两个子节点,而小于其根节点为止,从而达到使整个堆实现二叉堆的要求。
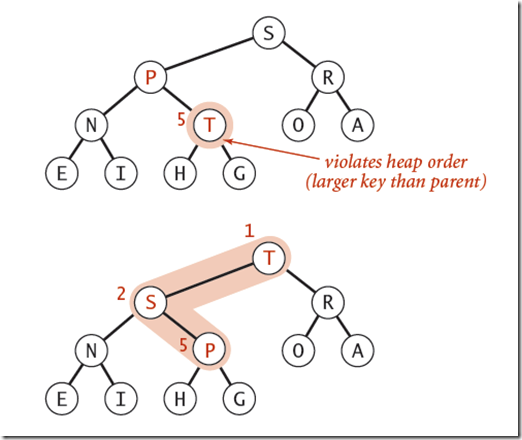
由上图可以看到,我们只需要将该元素k和其父元素k/2进行比较,如果比父元素大,则交换,然后迭代,一直到比父元素小为止。
private static void Swim(int k)
{
//如果元素比其父元素大,则交换
while (k > 1 && pq[k].CompareTo(pq[k / 2]) > 0)
{
Swap(pq, k, k / 2);
k = k / 2;
}
}
这样,往堆中插入新元素的操作变成了,将该元素从下往上重新建堆操作:
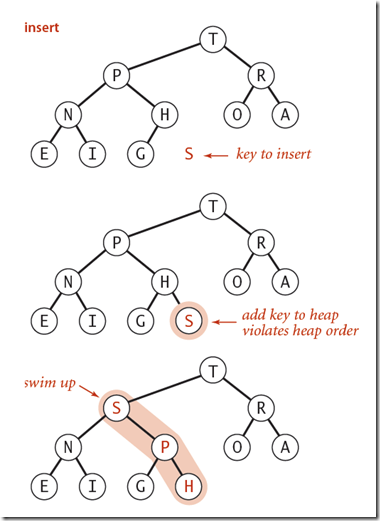
代码实现如下:
public static void Insert(T s)
{
//将元素添加到数组末尾
pq[++N] = s;
//然后让该元素从下至上重建堆
Swim(N);
}
动画如下:
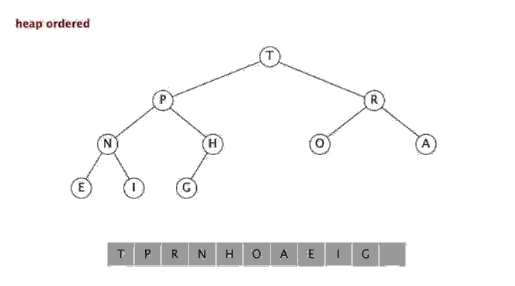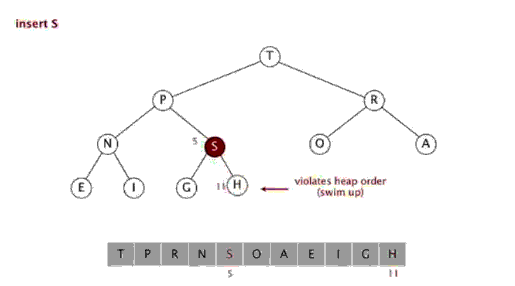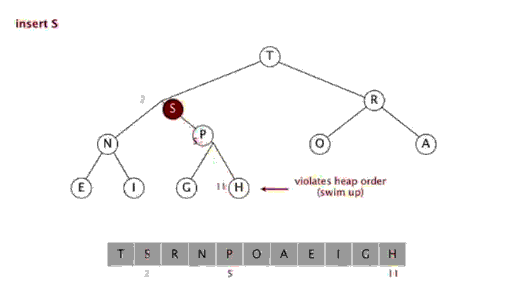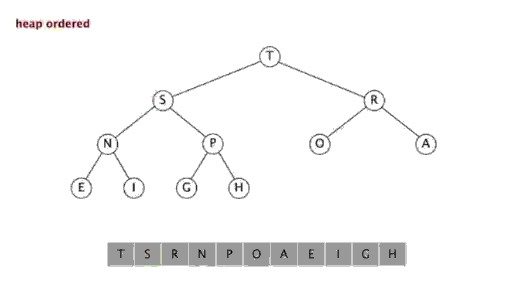
由上至下的重新建堆操作:当某一节点比其子节点要小的时候,就违反了二叉堆的定义,需要和其子节点进行交换以重新建堆,直到该节点都大于其子节点为止:
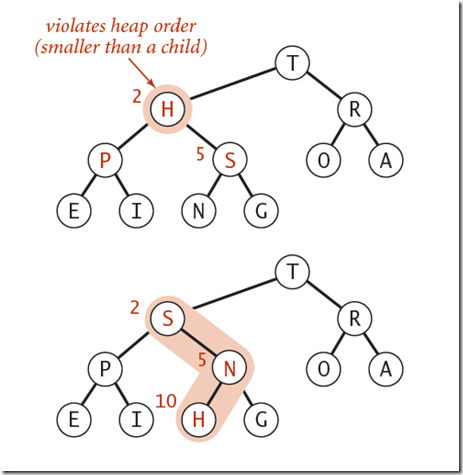
代码实现如下:
private static void Sink(int k)
{
while (2 * k < N)
{
int j = 2 * k;
//去左右子节点中,稍大的那个元素做比较
if (pq[j].CompareTo(pq[j + 1]) < 0) j++;
//如果父节点比这个较大的元素还大,表示满足要求,退出
if (pq[k].CompareTo(pq[j]) > 0) break;
//否则,与子节点进行交换
Swap(pq, k, j);
k = j;
}
}
这样,移除并返回最大元素操作DelMax可以变为:
1. 移除二叉堆根节点元素,并返回
2. 将数组中最后一个元素放到根节点位置
3. 然后对新的根节点元素进行Sink操作,直到满足二叉堆要求。
移除最大值并返回的操作如下图所示:
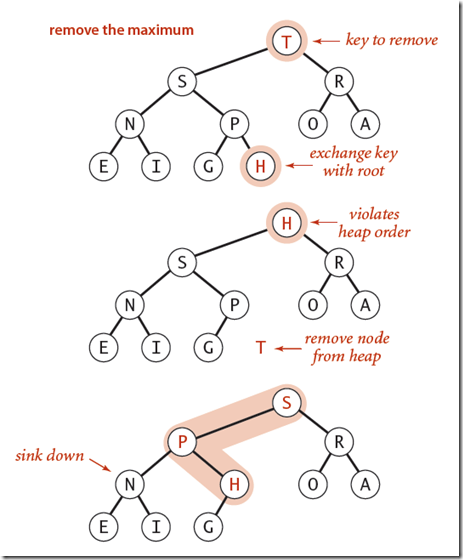
以上操作的实现如下:
public static T DelMax()
{
//根元素从1开始,0不存放值
T max = pq[1];
//将最后一个元素和根节点元素进行交换
Swap(pq, 1, N--);
//对根节点从上至下重新建堆
Sink(1);
//将最后一个元素置为空
pq[N + 1] = default(T);
return max;
}
动画如下:
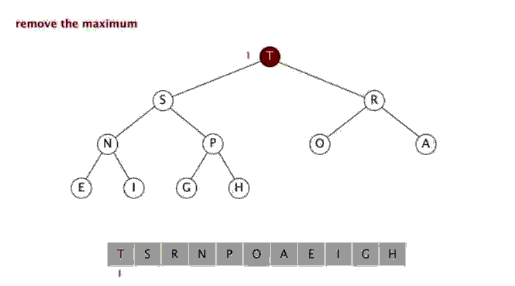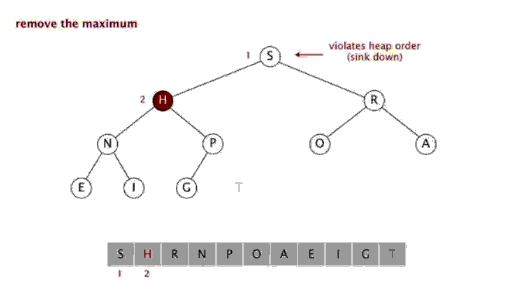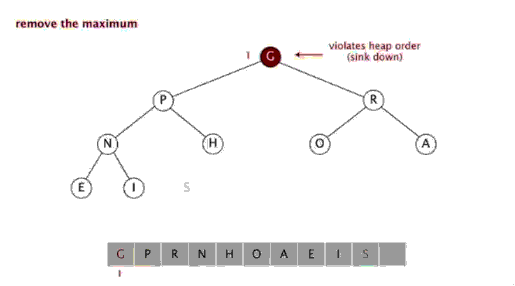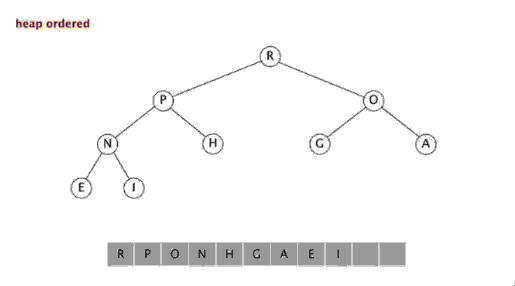
优先级队列Priority_queue的更多相关文章
- STL学习系列七:优先级队列priority_queue容器
1.简介 最大值优先级队列.最小值优先级队列 优先级队列适配器 STL priority_queue 用来开发一些特殊的应用,请对stl的类库,多做扩展性学习 这里给个例子: #include< ...
- C++ STL 学习笔记__(6)优先级队列priority_queue基本操作
10.2.7优先级队列priority_queue v 最大值优先级队列.最小值优先级队列 v 优先级队列适配器 STL priority_queue v 用来开发一些特殊的应用,请对stl的类 ...
- C++ - 库函数优先级队列(priority_queue)输出最小值 代码
库函数优先级队列(priority_queue)输出最小值 代码 本文地址: http://blog.csdn.net/caroline_wendy 库函数优先级队列(priority_queue)的 ...
- c++ 优先级队列(priority_queue)
从网上搜优先级队列用法,都是有些乱七八糟的,有几种用法都没说,直接贴代码.实在郁闷,于是自己在此归纳归纳. 废话不多说,直入主题. 优先级队列的核心是比较函数的实现. 比较函数有两种实现方法: 1.在 ...
- STL之优先级队列priority_queue
摘要: priority_queue,自适应容器(即容器适配器):不能由list来组建: 最大值优先级队列(最大值始终在对首,push进去时候) 最小值优先级队列: 优先级队列适配器 STL pri ...
- STL中的优先级队列priority_queue
priority_queue(queue类似)完全以底部容器为根据,再加上二叉堆(大根堆或者小根堆)的实现原理,所以其实现非常简单,缺省情况下priority_queue以vector作为底部容器.另 ...
- STL中的优先级队列(priority_queue)的自己实现priqueue
这篇文章主要介绍堆(最大堆和最小堆),以及一些系统对一些任务,比如线程,进程做调度的时候,所采用的优先级队列. 主要思想就是,做一个最大堆(任务的权重最大的在顶端),把顶端的任务取出,重新做一个堆,处 ...
- STL-优先级队列-priority_queue
头文件是<queue> 操作很简单 #include <iostream> #include <cstdio> #include <queue> usi ...
- cb05a_c++_STL优先级队列priority_queue_less_greater
/*cb05a_c++_STL优先级队列priority_queue自适应容器(容器适配器):不能使用list,list不能使用随机操作最大值优先级队列,//把数据放在队列里面是,最大的始终都是放在最 ...
随机推荐
- ASP.NET Core 四种释放 IDisposable 对象的方法
本文翻译自<Four ways to dispose IDisposables in ASP.NET Core>,由于水平有限,故无法保证翻译完全正确,欢迎指出错误.谢谢! IDispos ...
- 使用jQuery操作 DOM
DOM操作分为三类: 1.DOM Core:任何一种支持DOM的编程语言都可以使用它,如getElementById() 2.HTML-DOM:用于处理HTML文档,如document.forms 3 ...
- java的多线程初体验
这里以车站售票作为模拟场景,多个票务人员同时出售某一列高铁(G250?)的车票,售票的基本保证有2点: 1.不能售出多于预定限额的车票. 2.不能售出具有相同座位的车票. 初学java,有不当的地方各 ...
- YARN框架详解
YARN框架详解 YARN官方解释 YARN是什么 The fundamental(定义) idea of YARN is to split(分开) up the functionalities(功能 ...
- 我的学习之路_第二十八章_JQuery 和validator插件
jQuery 利用jQuery进行遍历 js原生: for(var i=0;i>?;i++){ } jQuery: 方式一: 想要遍历的jQuery对象.each(function(index, ...
- 使用C#在VS中开发:未处理AccessViolationException “System.AccessViolationException”类型的未经处理的异常
未处理AccessViolationException: “System.AccessViolationException”类型的未经处理的异常在System.Data.dll中发生 其他信息:尝试读 ...
- (转)linux中项目部署和日志查看
1 查找进程 ps -ef | grep java 查看所有关于java的进程 root 17540 1 0 2009 ? 01:42:27 /usr/java/ ...
- 唠一唠Linux系统入门的方法和经验
相信大伙都听说过linux系统,然而对于这个系统,总使让新手感觉茫然,偌大的系统.下面是一段百度中的介绍: Linux是一套免费使用和自由传播的类Unix操作系统,是一个基于POSIX和UNIX的多用 ...
- 使用pdfbox分页保存pdf为图片
一.背景 pdfbox作为Apache开源的PDF操作工具,允许创建新的PDF文档,操作现有文档,以及从文档中提取内容的能力.Apache PDFBox还包括一些命令行实用工具.本文楼主主要介绍其中的 ...
- maven单元测试设置代理
背景 环境需要设置代理才能够访问外部网络,如果只是运行java程序来访问网络,我们可以通过java -jar test.jar -DproxyHost=proxy_ip -DproxyPort=pro ...
