python3 第十章 - 如何进行进制转化

在计算机的世界里，2进制是主流，而在人类的自然世界中，10进制是主流，那么在这之间必然就会存在进制转化的问题。本章我们就来谈谈进制转化，也希望通过本章加深您对前些章所学知识的理解。

原理：先说说关于位权的概念，某进制计数制中各位数字符号所表示的数值，表示该数字符号值乘以一个与数字符号有关的常数，该常数称为 “位权 ” 。位权的大小是以基数为底，数字符号所处的位置的序号为指数的整数次幂。十进制数的百位、十位、个位、十分位的权分别是10的2次方、10的1次方、10的0次方，10的-1次方。二进制数就是2的n次幂。按权展开求和（按权相加）正是非十进制化十进制的方法。

1、其它进制转十进制

把二进制数首先写成加权系数展开式，然后按十进制加法规则求和：

例如：1101 = 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 1*8 + 1*4 + 0*2 + 1*1 = 8 + 4 + 0 + 1 = 13

同样的，八进制转十进制，也可以用按权相加法：

例如：0o12 = 1 * 8¹ + 2 * 8⁰ = 1 * 8 + 2 * 1 = 10

再来看看，十六进制转十进制，怎么用按权相加法：

例如：0x12 = 1 * 16¹ + 2 * 16⁰ = 1 * 16 + 2 * 1= 18

2、十进制转其它进制

众所周知，二进制的基数为2，我们十进制化二进制时所除的2就是它的基数。

我们先举个十进制整数转换为二进制整数的例子，假设十进制整数A化得的二进制数为edcba 的形式，那么用上面的方法按权展开， 得A=a(2^0)+b(2^1)+c(2^2)+d(2^3)+e(2^4) （后面的和不正是化十进制的过程吗）

假设该数未转化为二进制，除以基数2得
A/2=a(2^0)/2+b(2^1)/2+c(2^2)/2+d(2^3)/2+e(2^4)/2
注意：a除不开二，余下了！其他的绝对能除开，因为他们都包含2，而a乘的是1，他本身绝对不包含因数2，只能余下。
商得：
b(2^0)+c(2^1)+d(2^2)+e(2^3)，再除以基数2余下了b，以此类推。
当这个数不能再被2除时，先余掉的a位数在原数低，而后来的余数数位高，所以要把所有的余数反过来写。正好是edcba

我们先来看看，十进制如何转二进制，以13为例：

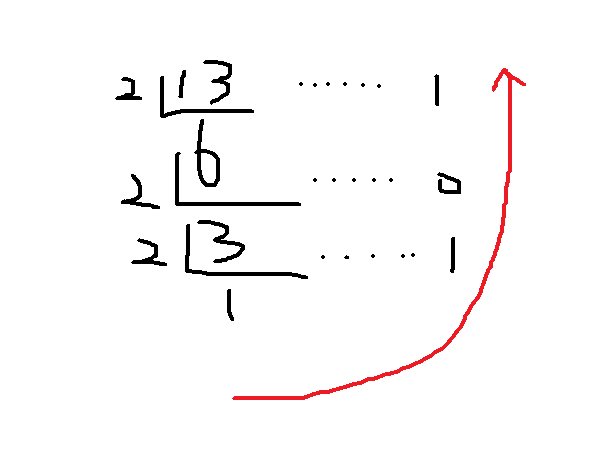
十进制整数转换为二进制整数采用”除2取余，逆序排列"法。具体做法是：用2整除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为0时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。

所以，13 = 0b1101

我们再来看看，十进制如何转八进制，以53为例：

十进制整数转换为八进制整数采用”除8取余，逆序排列"法。具体做法是：用8整除十进制整数，可以得到一个商和余数；再用8去除商，又会得到一个商和余数，如此进行，直到商为0时为止，然后把先得到的余数作为八进制数的低位有效位，后得到的余数作为八进制数的高位有效位，依次排列起来。

所以，153 = 0o231

通过以上十进制转二进制，以及十进制转八进制的例子，你应该明白规律了吧，自己试着把十进制286转成十六进制

3、十进制小数转换为二进制小数

十进制小数转换成二进制小数采用"乘2取整，顺序排列"法。具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，此时0或1为二进制的最后一位。或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。
十进制小数转二进制

如：0.625=0b0.101
0.625*2=1.25======取出整数部分1
0.25*2=0.5========取出整数部分0
0.5*2=1==========取出整数部分1

再如：0.7=0B0.1 0110 0110...
0.7*2=1.4========取出整数部分1
0.4*2=0.8========取出整数部分0
0.8*2=1.6========取出整数部分1
0.6*2=1.2========取出整数部分1
0.2*2=0.4========取出整数部分0
0.4*2=0.8========取出整数部分0
0.8*2=1.6========取出整数部分1
0.6*2=1.2========取出整数部分1
0.2*2=0.4========取出整数部分0

原理：
关于十进制小数转换为二进制小数
假设一十进制小数B化为了二进制小数0.ab的形式，同样按权展开，得
B=a(2^-1)+b(2^-2)
因为小数部分的位权是负次幂，所以我们只能乘2，得
2B=a+b（2^-1)
注意a变成了整数部分，我们取整数正好是取到了a，剩下的小数部分也如此。
值得一提的是，小数部分的按权展开的数位顺数正好和整数部分相反，所以不必反向取余数了。

如果小数的整数部分有大于0的整数时该如何转换呢？如以上整数转换成二进制，小数转换成二进制，然后加在一起就OK了，例如：6.125转成二进制

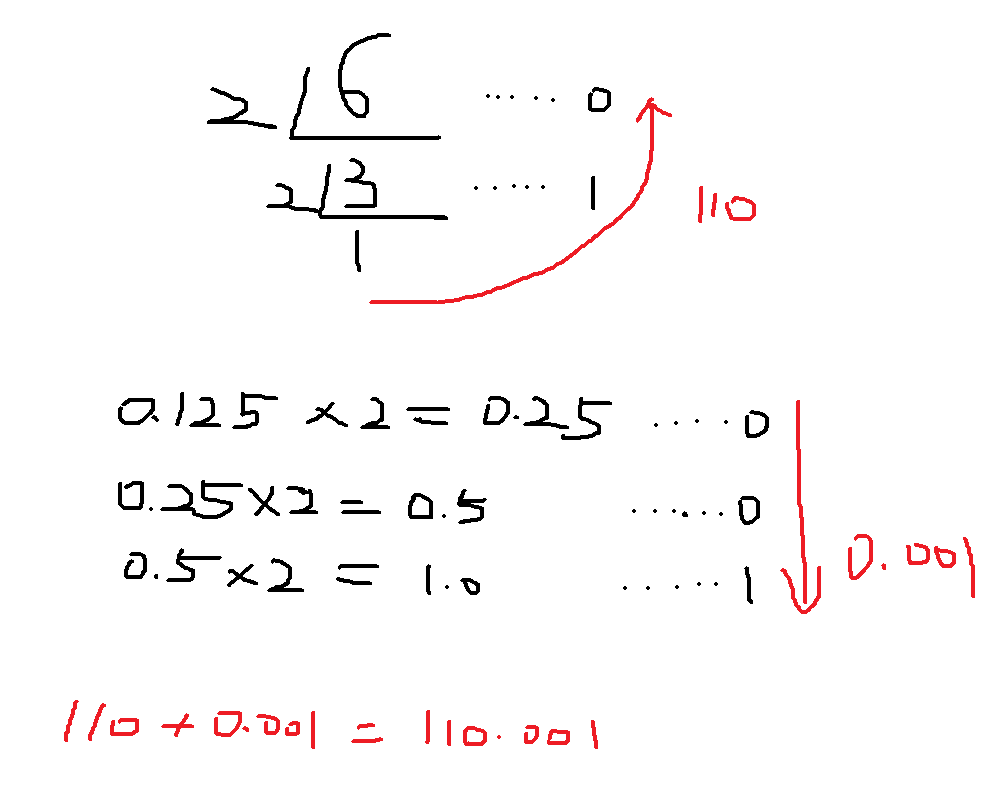
6.125 = 0B110.001

十进制小数转换为八进制小数、十进制小数转换为16进制小数也是类似的操作，请自行把 6.125分别转化为8进制、16进制

思考，如何把10进制转化为2~36的任意进制？后面的教程里，我们用程序来实现。

在线验证工具：http://tool.oschina.net/hexconvert/