bzoj2125 最短路

Description

给一个N个点M条边的连通无向图，满足每条边最多属于一个环，有Q组询问，每次询问两点之间的最短路径。

Input

输入的第一行包含三个整数，分别表示N和M和Q 下接M行，每行三个整数v，u，w表示一条无向边v-u，长度为w 最后Q行，每行两个整数v，u表示一组询问

Output

输出Q行，每行一个整数表示询问的答案

Sample Input

9 10 2
1 2 1
1 4 1
3 4 1
2 3 1
3 7 1
7 8 2
7 9 2
1 5 3
1 6 4
5 6 1
1 9
5 7

Sample Output

5
6

HINT

对于100%的数据，N<=10000，Q<=10000

正解：仙人掌+圆方树。

这道题直接判环好像很不好写的样子。。于是我去学了圆方树。

圆方树其实就是边双连通分量缩点。。把一个环上的点全部连到一个新点上，把这个点称作方点，其他点都是圆点。

不是环上的边就直接按照原图连就行了。

然后我们可以发现，这样得到的树和原来的仙人掌其实是等价的。

参见神犇博客：http://www.cnblogs.com/zzqsblog/p/5851393.html

蒯两个图：

仙人掌：

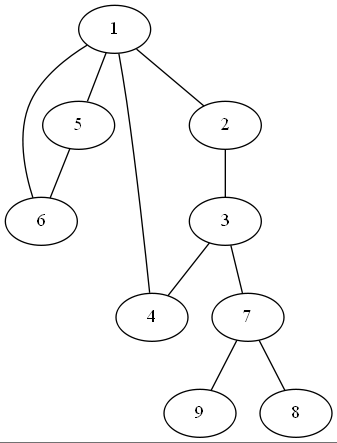
圆方树：

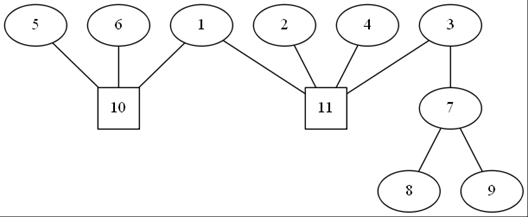
如何给这棵树设边权？如果是两个圆点之间的边，那么边权就是原边权，如果是圆方点之间的边，那么边权就是圆点到那个环顶的最短路径。

如何查询两点间最短路径？首先我们发现，如果两点的$LCA$是圆点，那么最短路就是两点之间距离，否则就要特判一下$LCA$的那两个儿子在环上的最短距离。

于是我们就能成功地解决仙人掌最短路问题了。

150行。。写得我要爽死了。。

 //It is made by wfj_2048~
 #include <algorithm>
 #include <iostream>
 #include <complex>
 #include <cstring>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <set>
 #define inf (1<<30)
 #define N (40010)
 #define il inline
 #define RG register
 #define ll long long
 #define File(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout)

 using namespace std;

 int n,m,q;

 struct edge{ int nt,to,dis; };

 struct YFtree{

     edge g[*N]; int head[N],top[N],fa[N],son[N],dep[N],tid[N],pos[N],sz[N],dis[N],D[N],fg[N],nn,num,cnt;

     il void insert(RG int from,RG int to,RG int dis){
     g[++num]=(edge){head[from],to,dis},head[from]=num; swap(from,to);
     g[++num]=(edge){head[from],to,dis},head[from]=num; return;
     }

     il void dfs1(RG int x,RG int p){
     fa[x]=p,dep[x]=dep[p]+,sz[x]=; RG int v;
     for (RG int i=head[x];i;i=g[i].nt){
         v=g[i].to; if (v==p) continue;
         dis[v]=dis[x]+g[i].dis;
         dfs1(v,x),sz[x]+=sz[v];
         if (sz[son[x]]<=sz[v]) son[x]=v;
     }
     return;
     }

     il void dfs2(RG int x,RG int p,RG int anc){
     top[x]=anc,tid[x]=++cnt,pos[cnt]=x;
     if (son[x]) dfs2(son[x],x,anc); RG int v;
     for (RG int i=head[x];i;i=g[i].nt){
         v=g[i].to; if (v==p || v==son[x]) continue;
         dfs2(v,x,v);
     }
     return;
     }

     il int lca(RG int u,RG int v){
     while (top[u]!=top[v]){
         if (dep[top[u]]<dep[top[v]]) swap(u,v);
         u=fa[top[u]];
     }
     return dep[u]<dep[v] ? u : v;
     }

     il int jump(RG int u,RG int Lca){
     RG int last;
     while (top[u]!=top[Lca])
         last=top[u],u=fa[top[u]];
     return u==Lca ? last : pos[tid[Lca]+];
     }

     il int query(RG int u,RG int v){
     RG int Lca=lca(u,v);
     if (Lca<=n) return dis[u]+dis[v]-*dis[Lca];
     RG int uu=jump(u,Lca),vv=jump(v,Lca);
     RG int du=dis[uu]-dis[Lca],dv=dis[vv]-dis[Lca];
     if (!fg[uu]) du=D[Lca]-du; if (!fg[vv]) dv=D[Lca]-dv;
     if (du>dv) swap(du,dv);
     return dis[u]-dis[uu]+dis[v]-dis[vv]+min(dv-du,D[Lca]-(dv-du));
     }

 }YF;

 struct Graph{

     edge g[*N]; int head[N],fa[N],dep[N],dis[N],dfn[N],low[N],st[N],num,cnt;

     il void insert(RG int from,RG int to,RG int dis){
     g[++num]=(edge){head[from],to,dis},head[from]=num; return;
     }

     il void dfs(RG int x,RG int p){
     fa[x]=p,dep[x]=dep[p]+,dfn[x]=low[x]=++cnt; RG int v;
     for (RG int i=head[x];i;i=g[i].nt){
         v=g[i].to; if (v==p) continue;
         if (!dfn[v]){
         dis[v]=dis[x]+g[i].dis,dfs(v,x);
         low[x]=min(low[x],low[v]);
         } else low[x]=min(low[x],dfn[v]);
         if (dfn[x]<low[v]) YF.insert(x,v,g[i].dis);
     }
     for (RG int i=head[x];i;i=g[i].nt){
         v=g[i].to; if (v==p) continue;
         if (fa[v]!=x && dfn[x]<dfn[v]) build(x,v,g[i].dis);
     }
     return;
     }

     il void build(RG int rt,RG int x,RG int d){
     RG int top=dep[x]-dep[rt]+,tot=d,Dis=;
     for (RG int i=x;i!=rt;i=fa[i])
         st[top--]=i,tot+=dis[i]-dis[fa[i]];
     YF.D[++YF.nn]=tot,st[]=rt,top=dep[x]-dep[rt]+;
     for (RG int i=;i<=top;++i){
         RG int dd=min(Dis,tot-Dis);
         YF.fg[st[i]]=dd==Dis;
         YF.insert(YF.nn,st[i],dd);
         Dis+=dis[st[i+]]-dis[st[i]];
     }
     return;
     }

 }G;

 il int gi(){
     RG int x=,q=; RG char ch=getchar();
     while ((ch<'' || ch>'') && ch!='-') ch=getchar();
     if (ch=='-') q=-,ch=getchar();
     while (ch>='' && ch<='') x=x*+ch-,ch=getchar(); return q*x;
 }

 il void work(){
     n=gi(),m=gi(),q=gi(); YF.nn=n;
     for (RG int i=,u,v,w;i<=m;++i){
     u=gi(),v=gi(),w=gi();
     G.insert(u,v,w),G.insert(v,u,w);
     }
     G.dfs(,); YF.dfs1(,); YF.dfs2(,,);
     for (RG int i=,u,v;i<=q;++i){
     u=gi(),v=gi();
     printf("%d\n",YF.query(u,v));
     }
     return;
 }

 int main(){
     File("shortest");
     work();
     return ;
 }