洛谷 P3384 【模板】树链剖分

树链剖分

将一棵树的每个节点到它所有子节点中子树和（所包含的点的个数）最大的那个子节点的这条边标记为“重边”。

将其他的边标记为“轻边”。

若果一个非根节点的子树的大小不小于任意一个他兄弟节点的子数大小（若有多个就看心情选取其中的一个），那么它到它父节点的连边为重边，这个节点为重子节点，否则，它到它父节点的连边为轻边。

将一条全部由重边组成的链叫做重链。

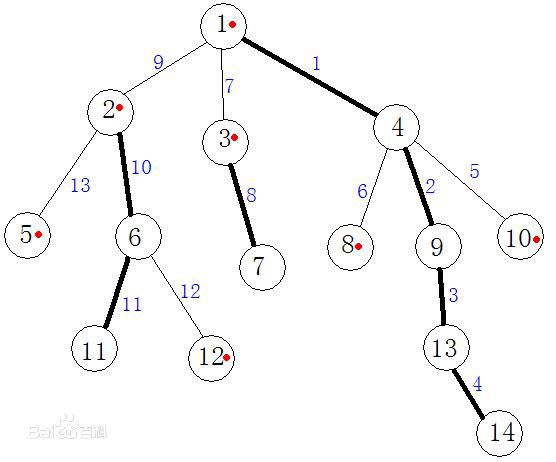
（图中加粗的边为重边，未加粗的边为轻边，图取自www.baidu.com）

这样做有什么用呢？

如上图剖分后的树有这样的性质：

1.每个点都在一条重链中（轻子节点所在重链链顶是它本身）

2.每一条重链一定是自上而下（即不会再一条重链上出现两个深度相同的点）

3.任意一个节点到根节点的路径上最多有log2(n)条轻边和log2(n)条重链。

这样之后，我们可以按照优先级为“根节点>重子节点>轻子节点”的顺序进行两次dfs，O(n)预处理出dfs序，深度，每个节点所在重链的顶端，这样就能保证每一条重链中所有的点的dfs序中的位置都是自上而下连续而递增的。

然后，我们再用一个线段树O（log2（n））维护每一条重链和轻边上点的权值的单点修改，区间修改，区间和、区间最值之类的问题。

如果要处理路径上的问题，我们可以不断将两个点中所在重链链顶深度小的那个点直接跳到它所在重链链顶的父节点，并对这条重链进行操作（如果这个点是轻子节点那么就直接对这个点进行操作），直到这两个点到达了同一条重链，这是再将两个点之间的部分进行操作。

这样，我们每次完成对一条路径的操作或询问复杂度为log2（n）乘以 log2（m）（m为每条链的平均长度，实际上这个数通常较小）。

这里附上洛谷模板题和AC代码。

题目描述

如题，已知一棵包含N个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

操作1： 格式： 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z

操作2： 格式： 2 x y 表示求树从x到y结点最短路径上所有节点的值之和

操作3： 格式： 3 x z 表示将以x为根节点的子树内所有节点值都加上z

操作4： 格式： 4 x 表示求以x为根节点的子树内所有节点值之和

输入输出格式

输入格式：

第一行包含4个正整数N、M、R、P，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含N个非负整数，分别依次表示各个节点上初始的数值。

接下来N-1行每行包含两个整数x、y，表示点x和点y之间连有一条边（保证无环且连通）

接下来M行每行包含若干个正整数，每行表示一个操作，格式如下：

操作1： 1 x y z

操作2： 2 x y

操作3： 3 x z

操作4： 4 x

输出格式：

输出包含若干行，分别依次表示每个操作2或操作4所得的结果（对P取模）

输入输出样例

输入样例：

5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

输出样例：

2
21

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #define LL long long
 #define mid (l+r>>1)
 #define len (r-l+1)
 #define M 100100
 using namespace std;
 LL read(){
     LL nm=,oe=;char cw=getchar();
     while(!isdigit(cw)) oe=cw=='-'?-oe:oe,cw=getchar();
     while(isdigit(cw)) nm=nm*+(cw-''),cw=getchar();
     return nm*oe;
 }
 LL n,m,f[M],fa[M],nt[M<<],to[M<<],tp[M],d[M],w[M];
 LL cnt,cur,mod,rt,a,b,sz[M],gt[M],ed[M],s[M],num,c[M];
 LL t[M<<],mk[M<<],add,typ;
 bool fg[M];
 void link(){nt[++cur]=f[a],f[a]=cur,to[cur]=b;}
 void dfs1(LL x){
     sz[x]=;
     int sn=;
     for(int i=f[x];i!=-;i=nt[i]){
         if(to[i]==fa[x]) continue;
         fa[to[i]]=x,d[to[i]]=d[x]+;
         dfs1(to[i]),sz[x]+=sz[to[i]];
         if(sn==) sn=i;
         else if(sz[to[sn]]<sz[to[i]]) sn=i;
     }
     if(sn!=) swap(to[f[x]],to[sn]),fg[to[f[x]]]=true;
     return;
 }
 void dfs2(int x){
     if(fg[x]) tp[x]=tp[fa[x]];
     else tp[x]=x;
     gt[x]=++cnt,s[gt[x]]=x;
     for(int i=f[x];i!=-;i=nt[i]){
         if(to[i]==fa[x]) continue;
         dfs2(to[i]);
     }
     ed[x]=cnt;
 }
 int build(int x,int l,int r){
     if(l==r) return t[x]=w[s[l]];
     return t[x]=(build(x<<,l,mid)+build(x<<|,mid+,r))%mod;
 }
 void pushdown(int x,int l,int r){
     mk[x<<]+=mk[x],t[x<<]+=(mid-l+)*mk[x];
     mk[x<<|]+=mk[x],t[x<<|]+=(r-mid)*mk[x];
     mk[x]=;
 }
 void update(int x,int l,int r,int L,int R){
     if(r<L||l>R) return;
     if(L<=l&&r<=R){
         mk[x]+=add;
         t[x]+=len*add;
         t[x]%=mod;
         return;
     }
     pushdown(x,l,r);
     update(x<<,l,mid,L,R);
     update(x<<|,mid+,r,L,R);
     t[x]=(t[x<<]+t[x<<|])%mod;
 }
 LL calc(int x,int l,int r,int L,int R){
     if(r<L||R<l) return ;
     if(L<=l&&r<=R) return t[x];
     pushdown(x,l,r);
     LL tot=calc(x<<,l,mid,L,R)+calc(x<<|,mid+,r,L,R);
     t[x]=(t[x<<]+t[x<<|])%mod;
     return tot%mod;
 }
 void change(){
     int x=a,y=b;
     while(tp[x]!=tp[y]){
         if(d[tp[x]]<d[tp[y]]) swap(x,y);
         update(,,n,gt[tp[x]],gt[x]),x=fa[tp[x]];
     }
     if(d[x]>d[y]) swap(x,y);
     update(,,n,gt[x],gt[y]);
     return;
 }
 LL ans(){
     LL tot=0ll,x=a,y=b;
     while(tp[x]!=tp[y]){
         if(d[tp[x]]<d[tp[y]]) swap(x,y);
         tot+=calc(,,n,gt[tp[x]],gt[x]),x=fa[tp[x]];
         tot%=mod;
     }
     if(d[x]>d[y]) swap(x,y);
     tot+=calc(,,n,gt[x],gt[y]);
     return tot;
 }
 int main(){
     n=read(),m=read(),rt=read(),mod=read();
     for(int i=;i<=n;i++) w[i]=read(),f[i]=-,fg[i]=false;
     for(int i=;i<n;i++){
         a=read(),b=read();
         link(),swap(a,b),link();
     }
     tp[rt]=fa[rt]=rt,d[rt]=;
     dfs1(rt),dfs2(rt),build(,,n);
     while(m--){
         typ=read(),a=read();
         if(typ==) b=read(),add=read(),change();
         else if(typ==) b=read(),printf("%lld\n",ans()%mod);
         else if(typ==) add=read(),update(,,n,gt[a],ed[a]);
         else printf("%lld\n",calc(,,n,gt[a],ed[a])%mod);
     }
     return ;
 }

本人代码风格较为奇怪，请大家见谅。