manim边做边学--圆环面

Torus类在制作数学、物理或工程领域的动画时具有广泛的应用场景。

比如，通过动态演示环面的拓扑变换（如内外翻转、扭曲等），帮助我们直观地理解拓扑不变量和同胚等概念；

此外，也可以模拟磁场线在环面导体中的分布和运动，展示电磁感应现象等等。

本篇介绍Torus的主要参数和基本使用方法。

1. 主要参数

Torus的参数不多，主要有：

参数名称	类型	说明
major_radius	float	圆环面的主要半径，从环面中心到其管道中心（或称为环面中心轴）的距离
minor_radius	float	环面管道的半径
resolution	[int, int]	环面表面的分辨率，用于控制渲染的精细程度
u_range	[float]	定义了圆环面在u方向上的参数化范围
v_range	[float]	定义了圆环面在v方向上的参数化范围

如果把Torus圆环面看成一个轮胎的话，

那么，major_radius参数表示轮胎的大小，minor_radius参数表示轮胎的厚度。

2. 使用示例

为了有效展示Torus（圆环面）各个参数的使用，下面构造四个示例，

每个示例将突出Torus类的一个或几个关键参数，并说明这些参数如何影响环面的外观和特性。

2.1. 标准圆环面

这是一个标准的环面，其中major_radius决定了环面的大小，minor_radius决定了环面管道的厚度，

而resolution控制了环面表面的平滑度。

通过调整这些参数，可以获得不同大小和形状的环面。

torus = Torus(
    major_radius=2.5,
    minor_radius=0.5,
    resolution=(30, 30),
)

2.2. 扁平圆环面

通过限制v_range的值，我们可以创建一个扁平的环面。

在这个示例中，v_range被设置为(0, PI/2)，这意味着环面在v方向上的参数化范围被限制在一个更小的区间内，从而导致环面在视觉上变得更加扁平。

这种扁平环面可以用于模拟轮胎、甜甜圈等扁平形状的物体。

torus = Torus(
    major_radius=2.5,
    minor_radius=0.5,
    resolution=(30, 30),
    v_range=(0, PI / 2),
)

2.3. 高分辨率圆环面

增加resolution的值可以提高环面表面的平滑度和细节程度。

在这个示例中，resolution被设置为(100, 100)，这意味着环面在u和v方向上都有更高的分辨率，从而呈现出更加细腻和逼真的曲面效果。

高分辨率环面在渲染复杂场景或制作高质量动画时非常有用。

torus = Torus(
    major_radius=2.5,
    minor_radius=0.5,
    resolution=(100, 100),
)

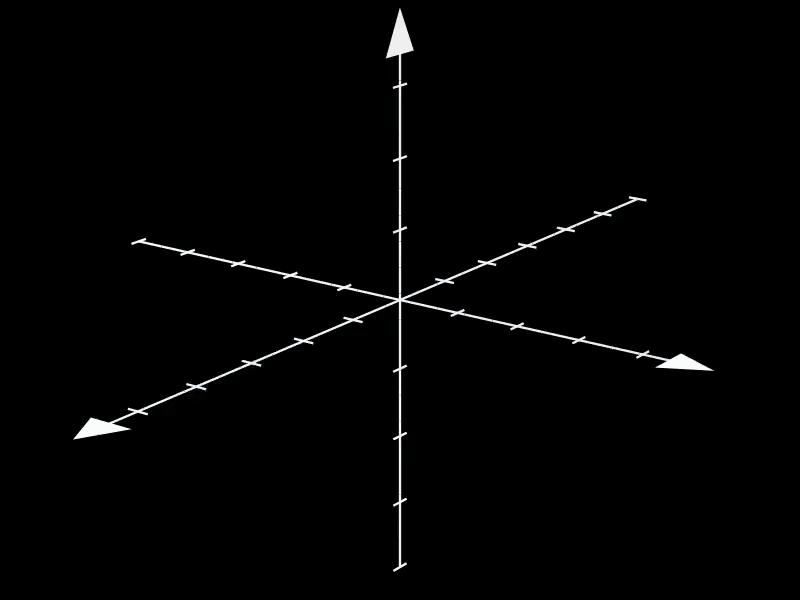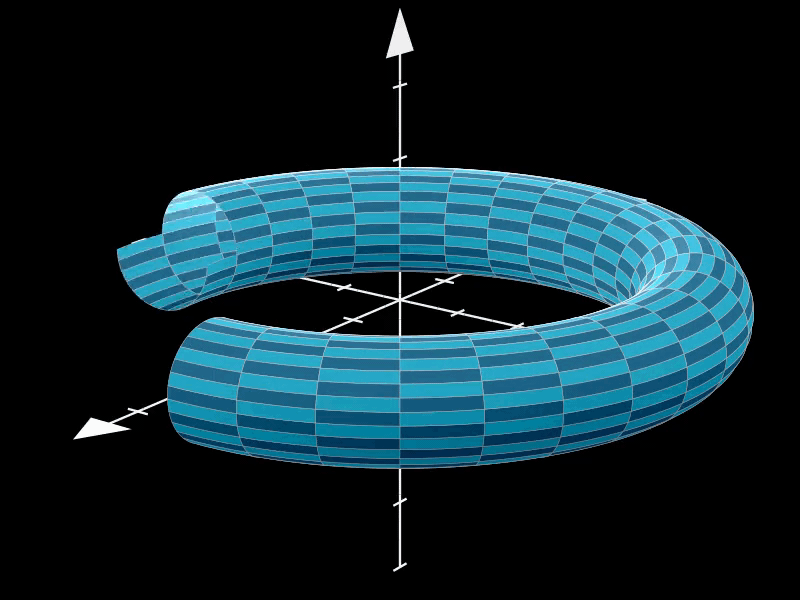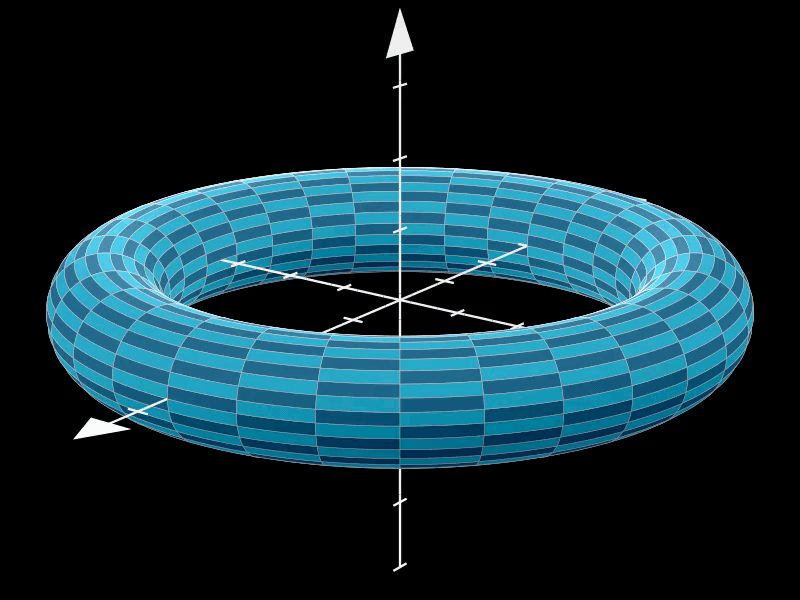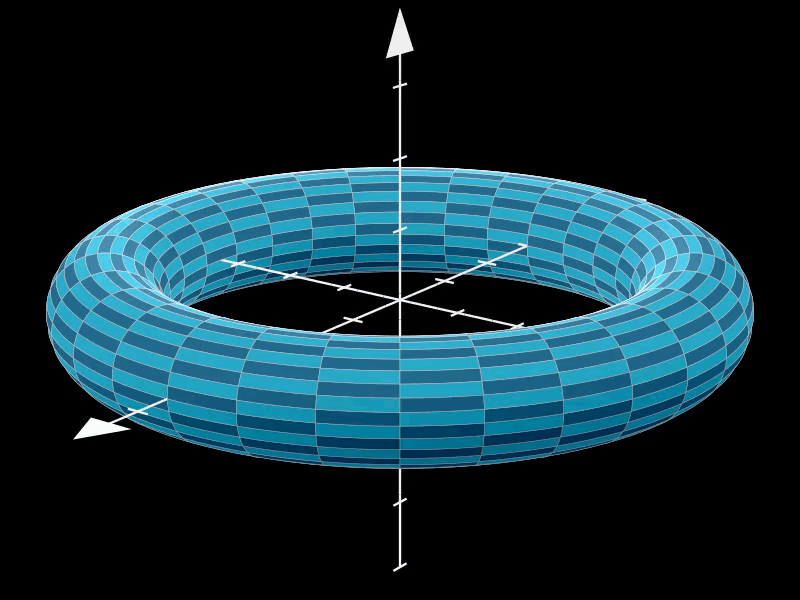
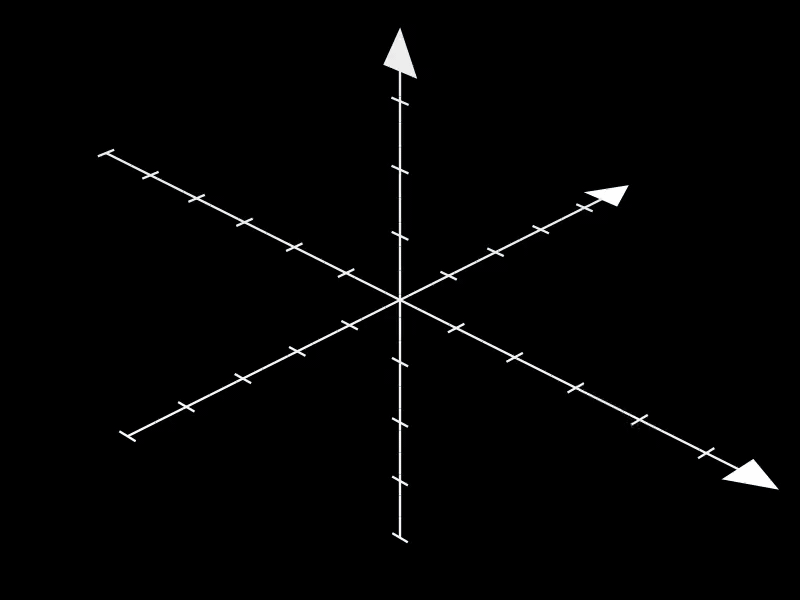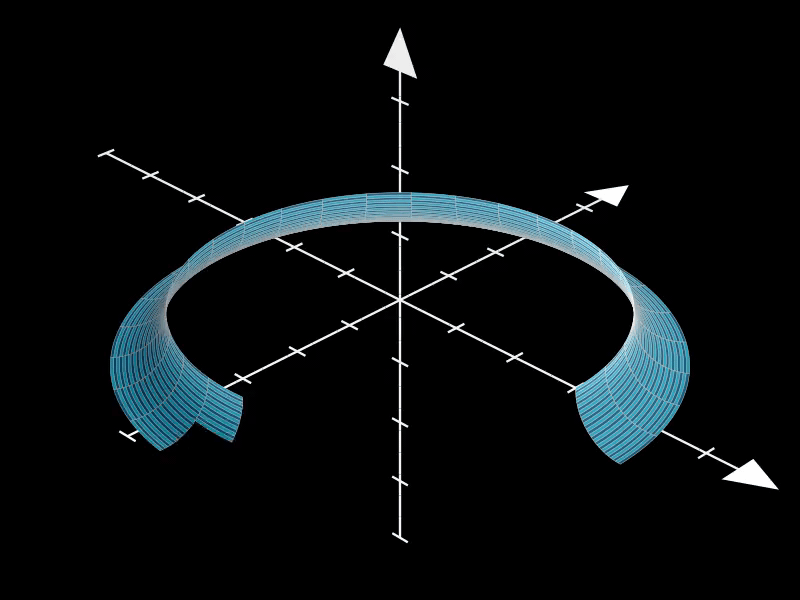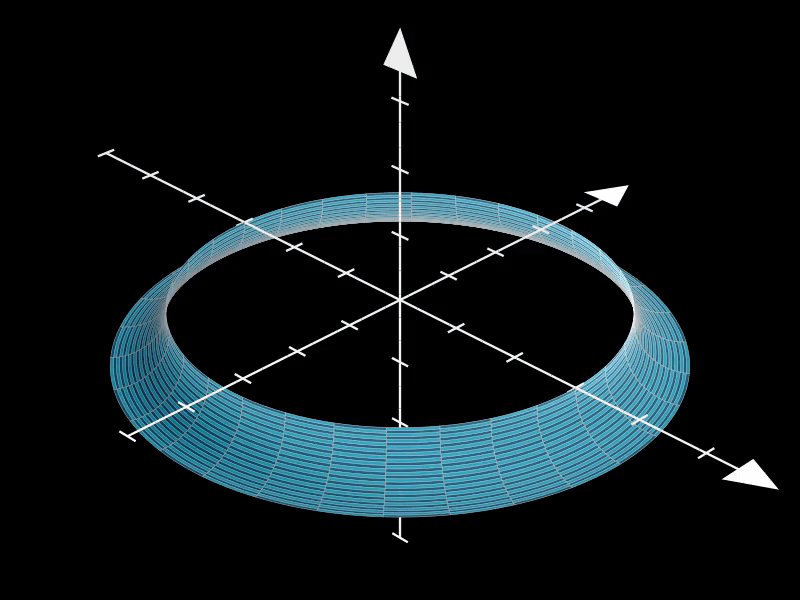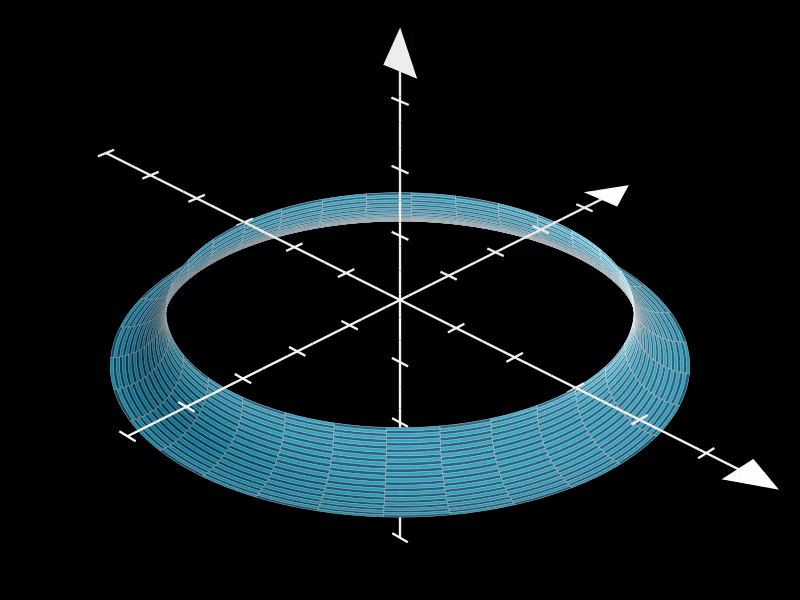
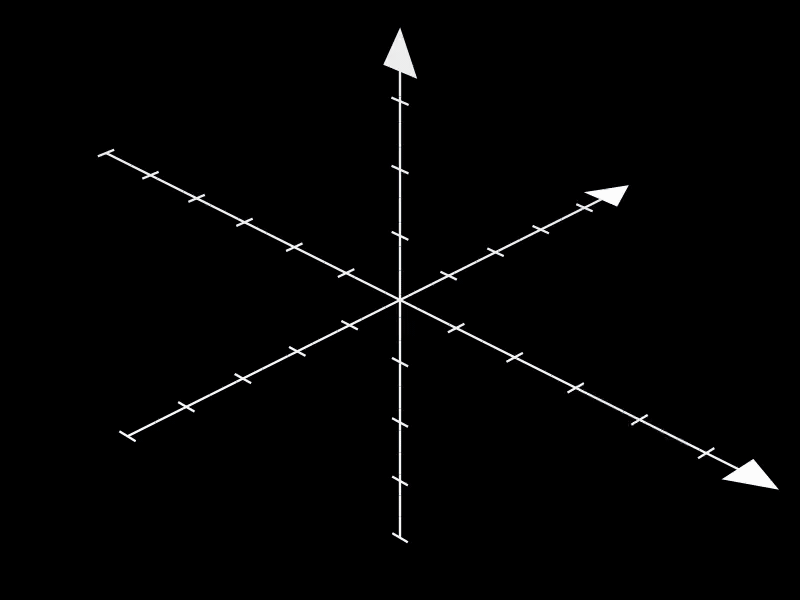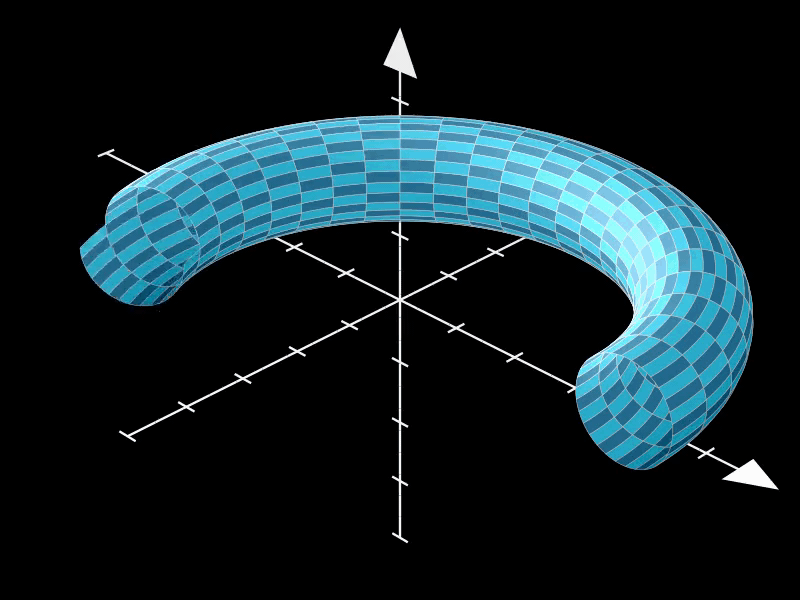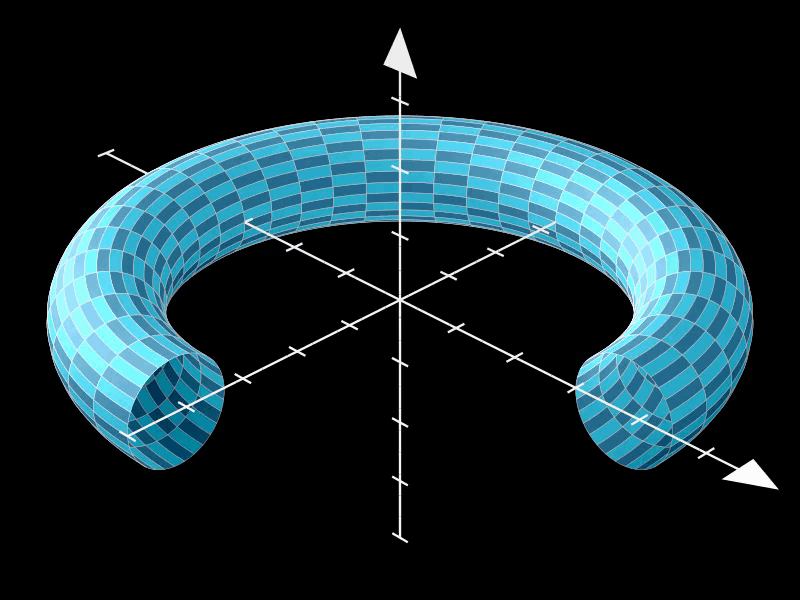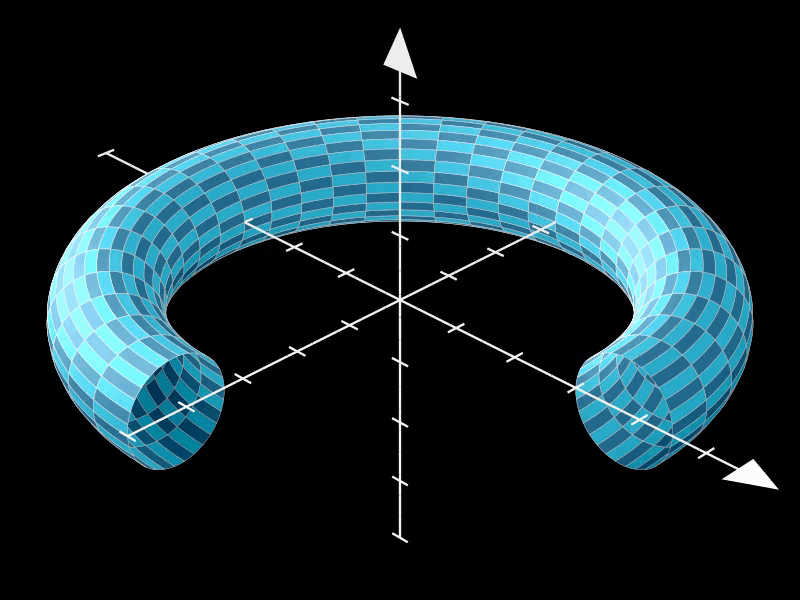
2.4. 非标准圆环面

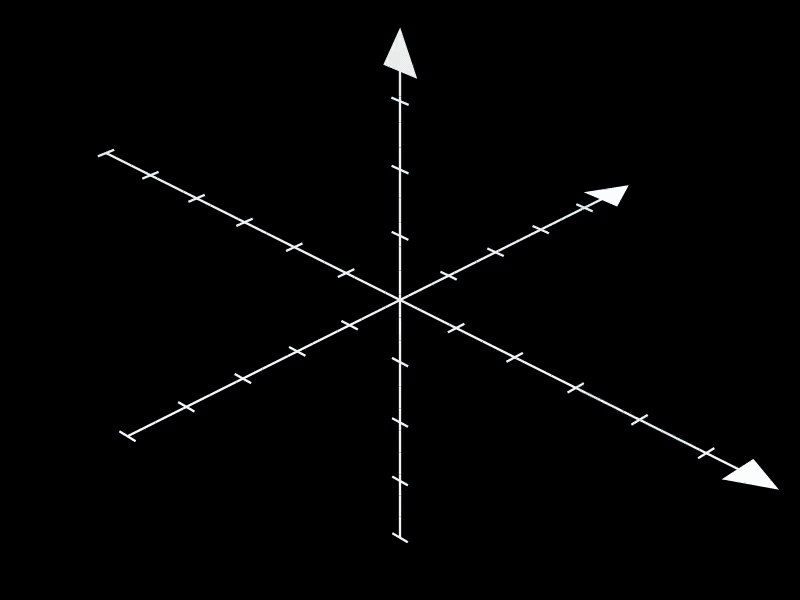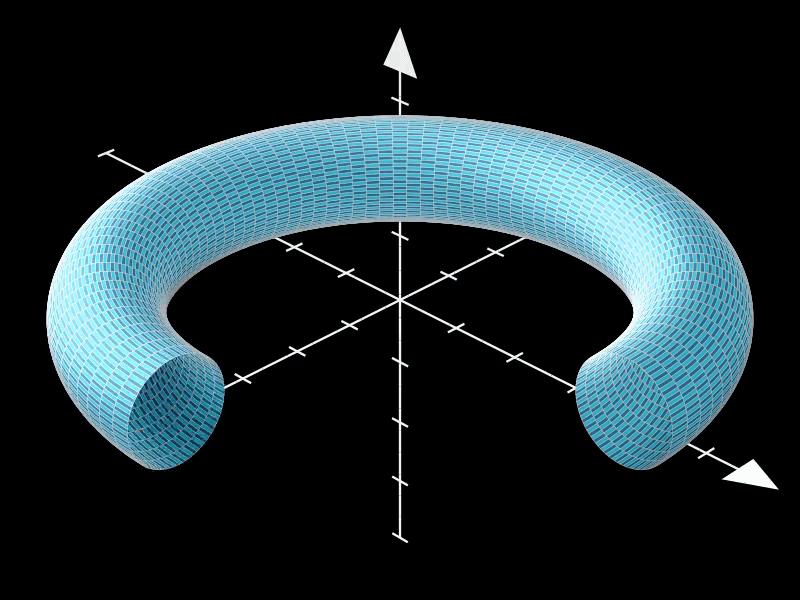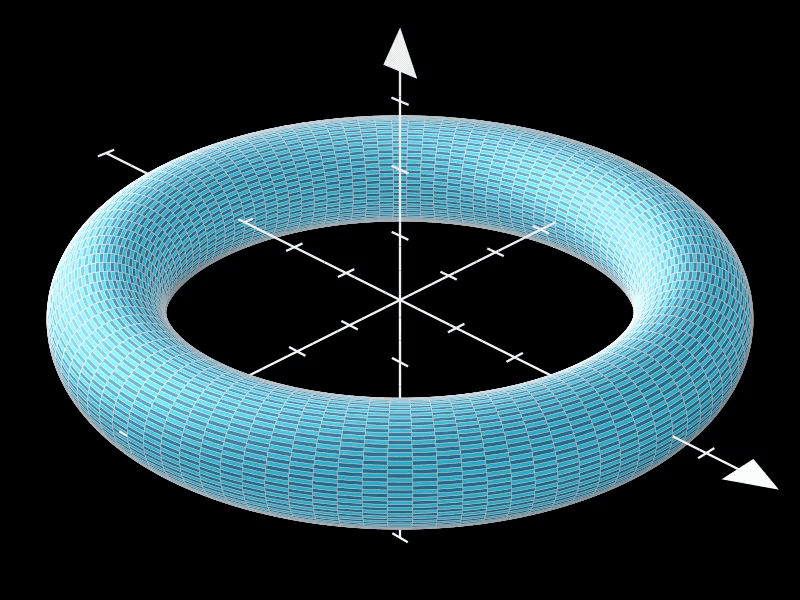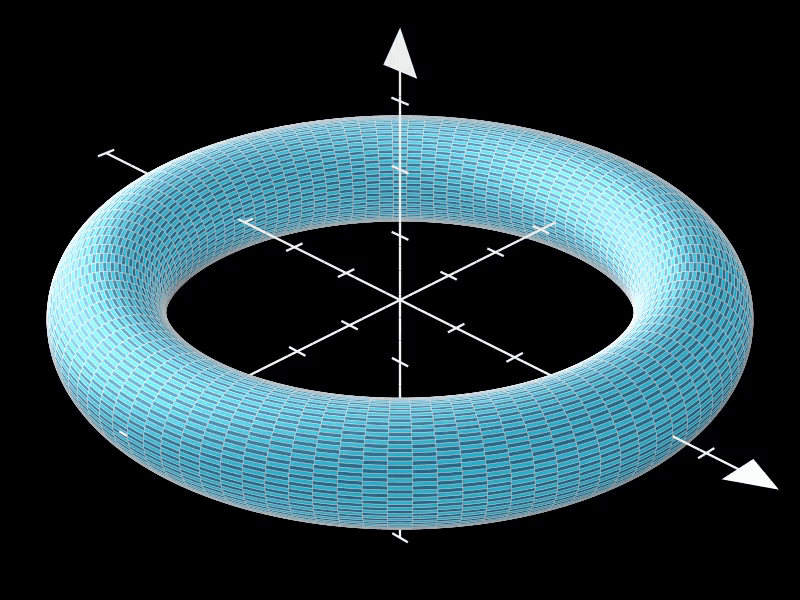
通过调整u_range的值，我们可以创建一个非标准的环面。

在这个示例中，u_range被设置为(0, 3*PI/2)，这意味着环面在u方向上的参数化范围被扩展到一个更大的区间内，从而导致环面在视觉上出现一部分缺失。

这种非标准环面可以用于艺术创作、数学可视化或物理模拟等领域，以展示环面在不同参数设置下的多样性和灵活性。

torus = Torus(
    major_radius=2.5,
    minor_radius=0.5,
    resolution=(30, 30),
    u_range=(0, 3 * PI / 2),
)

3. 附件

文中的代码只是关键部分的截取，完整的代码共享在网盘中（torus.py），

下载地址: 完整代码 (访问密码: 6872)