《University Calculus》-chape5-积分法-积分的定义

这一章节讨论积分的定义以及微积分基本定理。

笔者先前在数学证明专栏中关于高斯定理的证明的开头，给出了一段关于微积分思想的概括，文中提到根据导数(微分)的定义，根据其逆定义来给出积分的定义和计算方法，这里其实是及其不严谨的，积分本身有着自己的定义，而其计算方法正是微积分基本定理所呈现出来的东西。

积分的定义：

积分的现代定义的本质就是黎曼和，笔者之前关于多重积分定义的引入其实就已经提到过，这里是对一维的积分进行定义，相对二重、三重积分则会简单很多。

理论总是源于实际问题嘛，在解决曲线和坐标系围成的曲边梯形的面积的问题中，我们引入的积分。

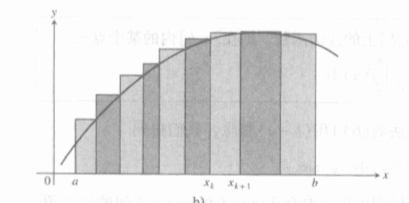
可以看到曲边梯形的面积可以近似的表示成如下的形式：

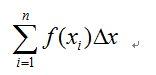
n趋于无穷之后便不再是近似相等而是严格相等。这边引入了积分符号

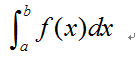
微积分的严格定义如下：

积分符号的详细解释：

依据定义我们能够得到它的如下运算性质：

充分理解积分概念对恰到好处的应用微积分非常重要，它的一个具体表现形式就是在一系列物理问题中，离散化的方程已经不能够适应我们对复杂问题的探究，这里就需要取一个积分变量dx列出存在积分的等式进行求解，而且对概念的充分理解也会有利于微积分的一系列高级应用——微分几何、偏微分、微分方程等中起到核心的作用。