【POJ2396】Budget（上下界网络流）

Description

We are supposed to make a budget proposal for this multi-site competition. The budget proposal is a matrix where the rows represent different kinds of expenses and the columns represent different sites. We had a meeting about this, some time ago where we discussed the sums over different kinds of expenses and sums over different sites. There was also some talk about special constraints: someone mentioned that Computer Center would need at least 2000K Rials for food and someone from Sharif Authorities argued they wouldn't use more than 30000K Rials for T-shirts. Anyway, we are sure there was more; we will go and try to find some notes from that meeting.

And, by the way, no one really reads budget proposals anyway, so we'll just have to make sure that it sums up properly and meets all constraints.

Input

The first line of the input contains an integer N, giving the number of test cases. The next line is empty, then, test cases follow: The first line of each test case contains two integers, m and n, giving the number of rows and columns (m <= 200, n <= 20). The second line contains m integers, giving the row sums of the matrix. The third line contains n integers, giving the column sums of the matrix. The fourth line contains an integer c (c < 1000) giving the number of constraints. The next c lines contain the constraints. There is an empty line after each test case.

Each constraint consists of two integers r and q, specifying some entry (or entries) in the matrix (the upper left corner is 1 1 and 0 is interpreted as "ALL", i.e. 4 0 means all entries on the fourth row and 0 0 means the entire matrix), one element from the set {<, =, >} and one integer v, with the obvious interpretation. For instance, the constraint 1 2 > 5 means that the cell in the 1st row and 2nd column must have an entry strictly greater than 5, and the constraint 4 0 = 3 means that all elements in the fourth row should be equal to 3.

Output

For each case output a matrix of non-negative integers meeting the above constraints or the string "IMPOSSIBLE" if no legal solution exists. Put one empty line between matrices.

Sample Input

2

2 3
8 10
5 6 7
4
0 2 > 2
2 1 = 3
2 3 > 2
2 3 < 5 

2 2
4 5
6 7
1
1 1 > 10

Sample Output

2 3 3
3 3 4 

IMPOSSIBLE 

 

【题意】

　　有一个n*m的方阵，里面的数字未知，但是我们知道如下约束条件：

　　每一行的数字的和

　　每一列的数字的和

　　某些格子有特殊的大小约束，用大于号，小于号和等于号表示

　　问：是否存在用正数填充这个方阵的方案，满足所有的约束，若有，输出之，否则输出IMPOSSIBLE。

【分析】

　　这题是有有源汇的上下界可行流，具体可看：http://blog.csdn.net/water_glass/article/details/6823741

　　

求解一个有上下界的网络流的步骤：

1.首先进行构图，对于那么对流量没有限制的边，我们直接将容量赋值为原始的容量，而对于有流量要求的边，我们将容量减去下界并将其等价与无下界的边。最后就是添加一个附
加汇点和一个附加源点，从附加源点连向每个顶点的容量为以该点所有流入的下界流量总和，每个顶点流向附加汇点是该点流出的下界流量总和。

2.我们要添加一条从汇点到源点流量为INF的边，这条边的意义在于，能够使得源点会汇点满足成为流量平衡条件的普通节点。

（以下为有上下界的最小流求解步骤）
3.我们在以附加源点和附加汇点求一次最大流，如果所有的到附加汇点的边都满载，那么说明这个网络是存在满足所有下界的可行流的。因为去除了下界容量的图具备这个能力。但
　是此时的可行流（从汇点流向源点的流量）并不一定是最小流，因为满足情况的可行流是不唯一的。

4.紧接着，我们在原图上从汇点向源点求一次最大流（此时要删除掉那条从汇点到源点的INF的边），此时便是一个缩流的过程，旨在试探图中是否还存在流量去替代汇点到源点的流量。这里计算出来的结果可能比我们已得到的可行流还要大，意思是说从汇点到源点有的是空间，因此也就不必连接那条INF的边了，整个网络的流量可以为0，网络中存在环流。

由于这里免不了会进行删边的操作，因此我们直接找到那条边，把流量赋值为0就可以了。

上述来自：http://www.cnblogs.com/proverbs/archive/2013/01/05/2846910.html

　　对于循环流上的某一条边x->y,下界为k1,上界为k2，我们这样变形，变成一个只有上界的网络流（下界默认为0），即普通的网络流，满流时有解。

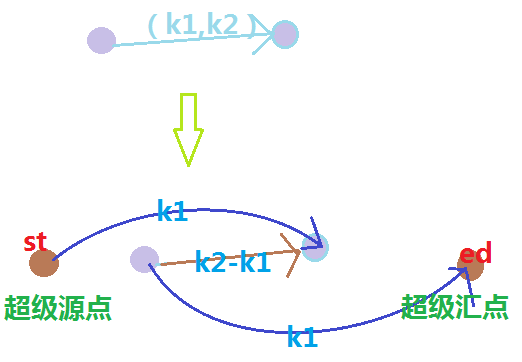
　　对于原图源汇的，我们在原图汇点连向原图源点一条流量为INF的边，形成循环流即可。

　　关于此题建模：类似二分图，每行建一个点，每列建一个点，源点连行，流量为这行的和，列连汇点，流量为这列的和。

　　行连向列的流量表示这行这列这个点的值。

　　根据题目中的约束求出边的上下界，跑一遍即可。

代码如下：

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 using namespace std;
 #define INF 0xfffffff
 #define Maxn 210
 #define Maxm 30

 int lim[][Maxn][Maxm];

 struct node
 {
     int x,y,next,f,o;
 }t[Maxn*Maxm*];int len;

 int first[Maxn*Maxn+],dis[Maxn*Maxm+];
 int st,ed,fst,fed,n,m,sum;
 bool ok;

 int mymax(int x,int y) {return x>y?x:y;}
 int mymin(int x,int y) {return x<y?x:y;}

 void ins(int x,int y,int f)
 {
     if(f==) return;
     if(x==fst) sum+=f;
     t[++len].x=x;t[len].y=y;t[len].f=f;
     t[len].next=first[x];first[x]=len;t[len].o=len+;
     t[++len].x=y;t[len].y=x;t[len].f=;
     t[len].next=first[y];first[y]=len;t[len].o=len-;
 }

 void get_e(int x,int y,int l1,int l2)
 {
     if(l2<l1) {ok=;return;}
     ins(fst,y,l1);ins(x,fed,l1);ins(x,y,l2-l1);
 }

 void init()
 {
     scanf("%d%d",&n,&m);
     memset(first,,sizeof(first));
     len=;
     st=n+m+;ed=st+;fst=ed+,fed=fst+;
     ok=;sum=;
     for(int i=;i<=n;i++)
     {
         int x;
         scanf("%d",&x);
         get_e(st,i,x,x);
     }
     for(int i=;i<=m;i++)
     {
         int x;
         scanf("%d",&x);
         get_e(i+n,ed,x,x);
     }
     int q;
     scanf("%d",&q);
     char s[];
     for(int i=;i<=n;i++)
      for(int j=;j<=m;j++)
      {
          lim[][i][j]=;lim[][i][j]=INF;
      }
     while(q--)
     {
         int x,y,z;
         scanf("%d%d%s%d",&x,&y,s,&z);
         int k1,k2,k3,k4;
         if(x==) k1=,k2=n;
         else k1=k2=x;
         if(y==) k3=,k4=m;
         else k3=k4=y;
         for(int i=k1;i<=k2;i++)
          for(int j=k3;j<=k4;j++)
          {
             if(s[]=='>') lim[][i][j]=mymax(lim[][i][j],z+);
             if(s[]=='=') lim[][i][j]=mymax(lim[][i][j],z);
             if(s[]=='<') lim[][i][j]=mymin(lim[][i][j],z-);
             if(s[]=='=') lim[][i][j]=mymin(lim[][i][j],z);
          }
     }
     for(int i=;i<=n;i++)
      for(int j=;j<=m;j++)
      {
          get_e(i,j+n,lim[][i][j],lim[][i][j]);
          if(ok==) break;
      }
     get_e(ed,st,,INF);
 }

 queue<int > q;
 bool bfs()
 {
     while(!q.empty()) q.pop();
     memset(dis,-,sizeof(dis));
     q.push(fst);dis[fst]=;
     while(!q.empty())
     {
         int x=q.front();q.pop();
         for(int i=first[x];i;i=t[i].next) if(t[i].f>)
         {
             if(dis[t[i].y]==-)
             {
                 dis[t[i].y]=dis[x]+;
                 q.push(t[i].y);
             }
         }
     }
     if(dis[fed]==-) return ;
     return ;
 }

 int ffind(int x,int low)
 {
     if(x==fed) return low;
     int now=;
     for(int i=first[x];i;i=t[i].next) if(t[i].f>)
     {
         int y=t[i].y;
         if(now==low) break;
         if(dis[y]==dis[x]+)
         {
             int a=mymin(t[i].f,low-now);
             a=ffind(t[i].y,a);
             t[i].f-=a;
             t[t[i].o].f+=a;
             now+=a;
         }
     }
     if(now==) dis[x]=-;
     return now;
 }

 int pri[Maxn][Maxm];
 void dinic()
 {
     int ans=;
     while(bfs())
     {
         ans+=ffind(fst,INF);
     }
     memset(pri,,sizeof(pri));
     if(ans==sum)
     {
         for(int i=;i<=len;i+=)
         {
             if(t[i].x>n&&t[i].x<=n+m&&t[i].y<=n+m)
             {
                 pri[t[i].y][t[i].x-n]=t[i].f;
             }
         }
         for(int i=;i<=n;i++)
         {
            for(int j=;j<=m;j++)
               printf("%d ",pri[i][j]+lim[][i][j]);
             printf("\n");
         }
     }
     else printf("IMPOSSIBLE\n");
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         init();
         if(ok==) {printf("IMPOSSIBLE\n\n");continue;}
         dinic();printf("\n");
     }
     return ;
 }

[POJ2396]

2016-05-19 17:01:02