算法打基础——顺序统计(找第k小数)

这次主要是讲如何在线性时间下找n个元素的未排序序列中第k小的数。当然如果\(k=1 or k=n\)，即找最大最小

数，线性时间内遍历即可完成，当拓展到一般，如中位数时，相关算法就值得研究了。这里还要说明的是，排序解

决是一种平凡算法，但其复杂度是\(\Theta(nlogn)\)

这次内容的主要知识点有：1.随机化版本的分治法求解&分析  2.基于1的优化pivot选择的算法&分析  

1.随机化版本的分治法求解与分析

首先，要明确的是现在我们要解决的问题是求解n元素序列的第k小数

这种方法的主要思想是：从序列中随机选一个数pivot，然后用类似于merge-sort的分割方法，将序列分成大于和小于pivot的两部分.

根据两边元素的数量，迭代的去求解，最终找到第k小元素. 下面给出伪代码：

RAND-SELECT(A, p, q, i)　　         ⊳ith smallest ofA[p..q]

　　if p= q　then returnA[p]

　　r←RAND-PARTITION(A, p, q)　⊳随机化分割子程序，返回处理完后pivot下标(分割见前面分治法)

　　k←r–p+ 1　　　　　　　          ⊳k 是 A[r]这个元素在子序列A[p~q]中的位置

　　if i== k then return A[r]

　　if i< k

　　　　then return RAND-SELECT(A, p, r –1, i)

　　　　else return RAND-SELECT(A, r + 1, q, i –k)

这里给出一个实例：

对这种随机化版本的分割进行分析，如果我们每次比较幸运分类的话：

T(n)=T(9n/10)+Θ(n)

=Θ(n)

如果每次分类都是最差情况的话(即0:n-1 split)

T(n)=T(n-1)+Θ(n)

=Θ(n²)   这种情况下比排序找这种平凡情况还要差

更具体的我们要分析随机版本运行的期望时间，因为数学公式多，所以这个就写在我的算法笔记里面了

结果最终肯定是Θ(n)!

2.基于1的优化pivot选择的算法&分析  

算法1是期望时间复杂度为O(n),那么存不存在最差情况都是O(n)的算法呢？ 由算法1，我们可以思考，是

什么导致了算法1的最差情况：是糟糕的划分。那么只要我们能找到一个好的划分方法，再基于算法1，就能

得到最差情况也是线性的算法了。

这里给出的Select算法就是这样的一个神奇的算法，这里先给出伪代码然后在用实例说明：

SELECT(i, n)

1.Divide the n elements into groups of 5. Find the median of each 5-element group by rote.

2.Recursively SELECT the median xof the floor{n/5} group medians to be the pivot.

3.Partition around the pivot x. Let k= rank(x).

4 if i= k then return x

elseif i< k

then recursively SELECT the ith

smallest element in the lower part

else recursively SELECT the (i–k)th

smallest element in the upper part

注意这个算法的3、4步和前面的算法是一样的，因为这个算法的主要目的是通过第1,2步找到一个分割的pivot

所以我们也着重分析1，2步

第一步：首先将序列按照5个一组进行分组，多出来的就不用管了； 然后通过随意什么方法找到5个元素中位数

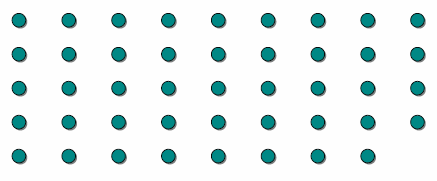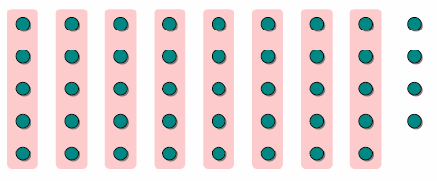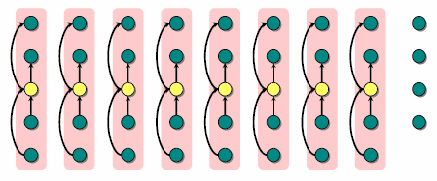
第二步：通过递归调用这个算法Select找到floor{n/5}个元素的中位数x,我们将这个数作为分割用的pivot

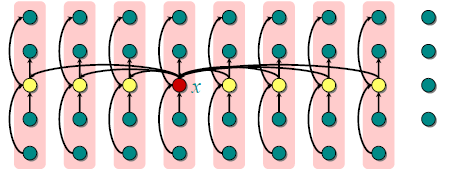
注意这里的箭头都是指向更小的数。然后我们来更具体的分析：

我们知道至少ceil{floor{n/5}/2}个中位数是不大于x的，那么必然有3floor{n/10}个值是不大于x的。同理，对称的也有那么多是不小于x的.

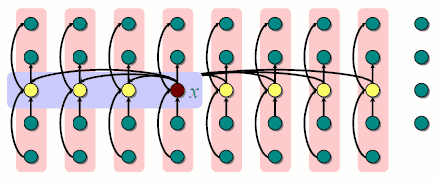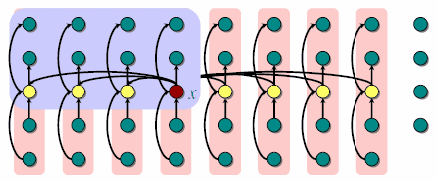
然后我们想让3floor{n/10}≥n/4,  当n≥50时是成立的。 也就是说这样分割一部分必然是≥4/n,即另一部分

小于等于3n/4. 就是说如果来处理的话不会超过T(3n/4)

然后我们来分析一下整个算法的复杂度：

step1 分割应该就是遍历过程Θ(n)

step2 递归解决n/5的问题 T(n/5)

step3 按照得到的pivot分割数组 Θ(n）

step4 递归解决分割的数组，最大不超过3n/4 T(3n/4)

故 T(n)=T(n/5)+T(3n/4)+Θ(n)

由替代法(其实就是n/5+3n/4=19/20n)，可以得到这个算法是线性的。

下面自己写的给出随机化算法的代码，第二个太懒了。。。还没写。写完会加上的

 /////////////////////////CLRS   video lec6  随机化版本的找第k大数/////////////////////////////////////////////////
 /// 运行时间的期望是O(n),最差情况O(n^2) /////////////////////////////////////////////////////

 #include<iostream>
 #include<cstdlib>
 #include<ctime>
 using namespace std;

 #define random(x)(rand()%x)

 void findkth(int* a,int s,int e,int k)
 {
     if(s>e) return;
     if(s==e)
     {
         cout<<a[s]<<endl;
         return;
     }
     int index=rand()%(e-s+);
     int pivot = a[s+index],temp;
     temp=a[s];a[s]=pivot;a[s+index]=temp;
     // 下面这一段做partition的工作
     int i=s,j;
     for(j=s+;j<=e;j++)
     {
         if(a[j]<pivot)
         {
             temp=a[++i];
             a[i]=a[j];
             a[j]=temp;
         }
     }
     temp=a[i];a[i]=pivot;a[s]=temp;
     if(i==k)
     {
         cout<<pivot<<endl;
         return;
     }
     else if(i<k)
     {
         findkth(a,i+,e,k);
     }
     else
     {
         findkth(a,s,i-,k);
     }
 }

 int main()
 {
     int a[];
     int i,j,k,index;
     srand(time());
     for(i=;i<;i++)
     {
         a[i]=random();
         cout<<a[i]<<" ";
     }
     cout<<endl;
     while(){
     cin>>k;
     findkth(a,,-,k);
     }
     return ;
 }

Rand_kth