【翻译】Longest Palindromic Substring 最长回文子串

原文地址：

http://articles.leetcode.com/2011/11/longest-palindromic-substring-part-i.html

转载请注明出处：http://www.cnblogs.com/zhxshseu/p/4947609.html

问题描述：Given a string S, find the longest palindromic substring in S.

这道题目是一个经典的动态规划DP http://challenge.greplin.com/问题，在面试中经常会被问到。为什么？因为这个问题可以有很多很多种解法。接下来将会给大家讲解5种解法，大家准备好了么？

 

你现在也可以先去 OJ 网站尝试去解决它。http://www.leetcode.com/onlinejudge

Hint:

首先，确认你能够理解 什么叫做 回文 palindrome。回文，就是一个正反向去读它，都是同一个结果的字符串。比如：“aba”是一个回文，但是“abc”不是。

一个普遍的错误:

有些朋友可能会立即想出一个快速的方法，但非常不幸，这个方法是不正确的。该方法描述如下：

把字符串S 反转，变成 S'，然后找到最长的公共子串不就好了么？https://en.wikipedia.org/wiki/Longest_common_substring_problem

看起来是正确的，并没有什么不妥。但是我们看下面的例子：

 

S = “caba”, S’ = “abac”.

S和S'的最大公共子串是aba，就是正确的答案。

但是看另一个例子：

S = “abacdfgdcaba”, S’ = “abacdgfdcaba”.

这个算法将会得出S的最大回文是“abacd”，显然是不正确的。

接下来给出一个O(N²) DP 解法，同时空间复杂度也是O(N²)。

暴力搜索Brute force solution, O(N³):

暴力算法是对所有的子串，判断是否是回文。对于一个长度为N的字符串，其子串总共有C(N,2)种，而判断子串是否是回文，时间复杂度为O(N)，所以总共耗费O(N³)时间.

动态规划解法, O(N²)时间复杂度 O(N²)空间复杂度:

为了将算法从暴力解法提升到DP解法，首先我们需要知道解法中得递推关系。比如字符串“ababa”，如果我们已经知道“bab”是回文，那么显然“ababa”也是回文，因为首字符和尾字符是相等的。

 

这样我们便知道了递推关系，描述如下：

定义 P[ i, j ] ← 如果子串S_i … S_j 是一个回文，那么该项为true, 否则为false.

因此递推如下：

P[ i, j ] 为 true ← ( P[ i+1, j-1 ]为true，并且S_i = S_j )

基本条件是：

P[ i, i ] 一定是true

P[ i, i+1 ] 为true ← ( S_i = S_i+1 )

这便是一个典型的DP问题解法。首先初始化长度为1,2的回文字符判断表，即P。然后以它为基础，逐个找出长度为3,4,5……的回文。（至于什么是DP问题，可以参看这篇文章http://www.360doc.com/content/13/0601/00/8076359_289597587.shtml）

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

string longestPalindromeDP(string s) {   int n = s.length();   int longestBegin = 0;   int maxLen = 1;   bool table[1000][1000] = {false};   for (int i = 0; i < n; i++) {     table[i][i] = true;   }   for (int i = 0; i < n-1; i++) {     if (s[i] == s[i+1]) {       table[i][i+1] = true;       longestBegin = i;       maxLen = 2;     }   }   for (int len = 3; len <= n; len++) {//对长度为3,4,5……的子串进行遍历     for (int i = 0; i < n-len+1; i++) {//以len为窗口，在s上进行平移，判断是否符合递推条件       int j = i+len-1;       if (s[i] == s[j] && table[i+1][j-1]) {         table[i][j] = true;         longestBegin = i;         maxLen = len;       }     }   }   return s.substr(longestBegin, maxLen); }

举例：cabccbad

第一次循环以后，table值如下

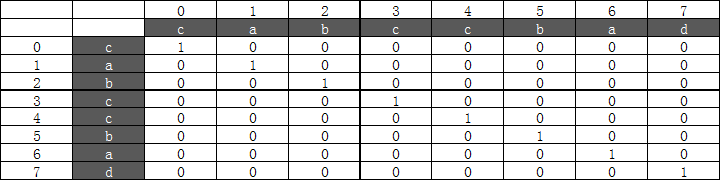
第二次循环以后，table值如下：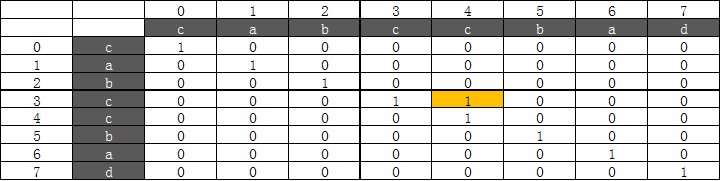

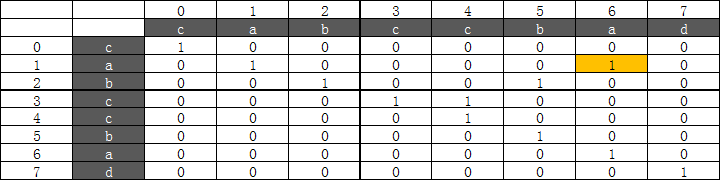
下面开始长度为3,4,5……的循环：

首先当len=3：

　　

     窗口里的子串为cab，i=0，j=2，这时候判断 Table[1][1] 是否 true（是），并且 s[0] 和 s[2] 是否相等（ 不相等）所以不满足。窗口平移：

　　

     一样的判断，同理还是不满足。

……

len=3循环结束，table值不变，因为没有长度为3的回文串。

len=4：

 　

     窗口子串为”cabc“，此时i=0，j=3，Table[1][2] false，不匹配。窗口平移。

    

     窗口子串为”abcc“，此时i=1，j=4，Table[2][3] false，不匹配。窗口平移。

　 

     窗口子串为”bccb“，此时i=2，j=5，Table[3][4] true，且 s[2]==s[5]，maxlen=4，longestBegin=2，Table更新

　　

     后面都不更新。

len=5：都不更新

len=6：

     当窗口滑到

　

     串口子串为”abccba“，此时i=1，j=6，Table[2][5] true，且 s[1]==s[6]，maxlen=6，longestBegin=1，Table更新

len=7：都不更新。

还有更简单的方法, O(N²) 时间复杂度 and O(1) 空间复杂度:

事实上我们可以在O(N²)时间复杂度的前提下，不使用额外的存储空间。

可以观察到，一个回文是以中心点，镜像对称的。因此，一个回文可以从中心点展开，而这个中心点，有2N-1个。

可能你会问，为什么是2N-1个中心点，而不是N个。这是因为偶数串中心点是两个数中间，奇数串中心点是中间的数字。

因为在一个中心点展开回文，需要耗时O(N)，总共时间复杂度也就是O(N²).

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

string expandAroundCenter(string s, int c1, int c2) {   int l = c1, r = c2;   int n = s.length();   while (l >= 0 && r <= n-1 && s[l] == s[r]) {     l--;     r++;   }   return s.substr(l+1, r-l-1); }   string longestPalindromeSimple(string s) {   int n = s.length();   if (n == 0) return "";   string longest = s.substr(0, 1);  // c single char itself is a palindrome   for (int i = 0; i < n-1; i++) {//遍历整个字符串     string p1 = expandAroundCenter(s, i, i);//以该位置字符为中心展开，奇数长     if (p1.length() > longest.length())       longest = p1;       string p2 = expandAroundCenter(s, i, i+1);//以该字符后面的空隙展开，偶数长     if (p2.length() > longest.length())       longest = p2;   }   return longest; }

举例：cabccbad

初始时，i=0 （奇 代表奇数长子串，偶 代表偶数长子串）

　 奇：

          一次循环，l=-1，r=1

          s.substr(l+1,r-l-1)==s.substr(0,1)，即”c“->longest

     偶：

          不满足循环条件，l=0，r=1

          substr(1,0) null.

i=1:

     奇：

           同上

     偶：

           同上

……

i=3：

     奇：

          同上

     偶：

          可以看出这是回文的对称点。

          循环三次，第四次判断结束。

          l=0，r=7

          substr(1，6）：”abccba“ -> longest

……

 

 

进一步思考:

存在 O(N)的算法么？显然有！ 关于 O(N)的解法将在下一篇中解答。http://articles.leetcode.com/2011/11/longest-palindromic-substring-part-ii.html