【数据结构与算法】字符串匹配（Rabin-Karp 算法和KMP 算法）

Rabin-Karp 算法

概念

用于在 一个字符串 中查找 另外一个字符串 出现的位置。

与暴力法不同，基本原理就是比较字符串的 哈希码 ( HashCode ) , 快速的确定子字符串是否等于被查找的字符串

比较哈希值采用的是滚动哈希法

• 如何计算哈希值：
  
  如 : “abcde” 的哈希码值为

\[a×31^4+b×31^3+c×31^2+d×31^1+e×31^0
\]

• 滚动哈希法：
  
  母串是"abcde"，子串是"cde"
  
  则母串先计算"abc"的哈希值：

  \[a×31^2+b×31^1+c×31^0
  \]

  而子串"cde"的哈希值是：

  \[c×31^2+d×31^1+e×31^0
  \]

  与母串哈希值不匹配，于是母串向后继续计算哈希值,下标i=3指向字母d，

  \[(a×31^2+b×31^1+c×31^0)×31+d-a×31^3
  \]

  前n个字符的hash * 31-前n字符的第一字符 * 31的n次方（n是子串长度）
  
  可以计算出母串中"bcd"的哈希值，再与子串哈希值进行比较

代码实现

    public static void main(String[] args) {
        String s = "ABABABA";
        String p = "ABA";
        match(p, s);
    }
    //p是母串，s是子串
    private static void match(String p, String s) {
        long hash_p = hash(p);//p的hash值
        long[] hashOfS = hash(s, p.length());
        match(hash_p, hashOfS);
    }

    private static void match(long hash_p, long[] hash_s) {
        for (int i = 0; i < hash_s.length; i++) {
            if (hash_s[i] == hash_p) {
                System.out.println(i);
            }
        }
    }
    final static long seed = 31;
    /**
     * n是子串的长度
     * 用滚动方法求出s中长度为n的每个子串的hash,组成一个hash数组
     */
    static long[] hash(final String s, final int n) {
        long[] res = new long[s.length() - n + 1];
        //前m个字符的hash
        res[0] = hash(s.substring(0, n));
        for (int i = n; i < s.length(); i++) {
            char newChar = s.charAt(i);
            char ochar = s.charAt(i - n);
            //前n个字符的hash*seed-前n字符的第一字符*seed的n次方
            long v = (res[i - n] * seed + newChar - pow(seed, n) * ochar) % Long.MAX_VALUE;  //防止溢出
            res[i - n + 1] = v;
        }
        return res;
    }
    static long pow(long a,int b){
        long ans = 1;
        while(b>0){
            ans*=a;
            b--;
        }
        return ans;
    }
    /**
     * 使用100000个不同字符串产生的冲突数，大概在0~3波动，使用100百万不同的字符串，冲突数大概110+范围波动。
     * 如果数据量非常大，可以在子串和母串哈希值匹配成功的时候多进行一步朴素的字符串比较，以防万一。
     */
    static long hash(String str) {
        long h = 0;
        for (int i = 0; i != str.length(); ++i) {
            h = seed * h + str.charAt(i);
        }
        return h % Long.MAX_VALUE;
    }

时间复杂度分析

设母串长度为m，子串长度为n。

则滚动计算母串哈希值复杂度是O(m)

计算子串哈希值复杂度是O(n)

遍历母串进行哈希值匹配的复杂度是O(m)

综上，Rabin-Karp算法的时间复杂度是O(m+n)

KMP 算法

概念

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称KMP算法）。

主要用于在文本串S中查找模式串P出现的位置。

• KMP和暴力匹配的不同
  
  

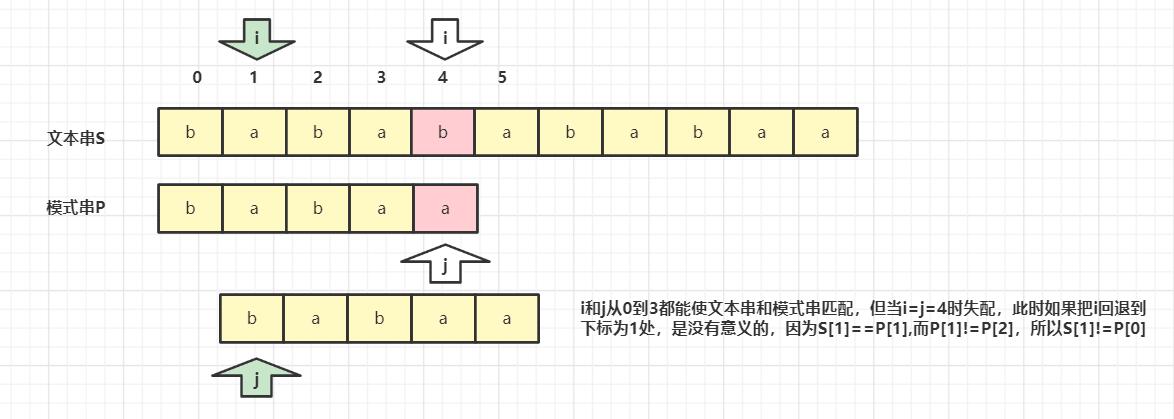
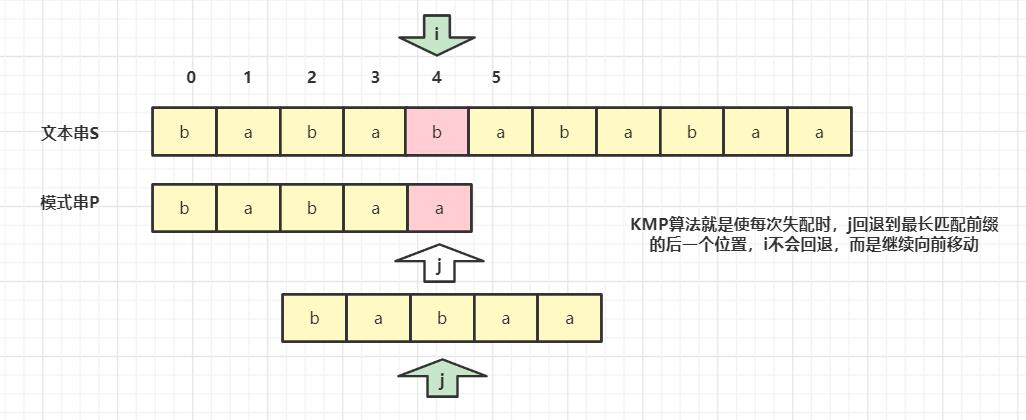
• 如何求解next数组

代码实现

public static void main(String[] args) {
        String src = "babababcbabababb";
        String p = "bababb";
        int index = kmp(src, p);
        System.out.println(index);
    }
    //s是文本串，p是模式串
    private static int kmp(String s, String p) {
        if (s.length() == 0 || p.length() == 0) return -1;
        if (p.length() > s.length()) return -1;
        int[] next = next(p);
        int i = 0;  //文本串的下标
        int j = 0;  //模式串的下标
        int slength = s.length();
        int plength = p.length();
        while (i < slength) {
            //①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++
            //j=-1，因为next[0]=-1,说明p的第一位和i这个位置无法匹配，这时i，j都增加1，i移位，j从0开始
            if (j == -1 || s.charAt(i) == p.charAt(j)) {
                i++;
                j++;
            } else {
            //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]回退
            //next[j]即为j所对应的next值
                j = next[j];
            }
            if (j == plength) {  //匹配成功了
                return i - j;
            }
        }
        return -1;
    }

    private static int[] next(String p) {
        int[] next = new int[p.length() + 1];
        int left = -1;
        int right = 0;
        next[0] = -1;
        while (right < p.length()) {
            if (left == -1 || p.charAt(left) == p.charAt(right)) {
                next[++right] = ++left;  //最长匹配位置加一
            } else {
                left = next[left];  //前缀回退到上一个最长匹配位置
            }
        }
        return next;
    }

KMP算法改进（nextval数组）

可以把next数组改造成nextval数组

下标（j)	0	1	2	3	4	5	6
模式串（P）	a	b	c	d	a	b	d
next	-1	0	0	0	0	1	2
nextval	-1	0	0	0	-1	0	2

当 j 处模式串字符不等于next[j]处模式串字符时，nextval[j]=next[j]

当 j 处模式串字符等于next[j]处模式串字符时，nextval[j]=nextval[next[j]]

比如：

下标为j=4处的模式串字符是a，而下标为next[j]处的模式串字符也是a，则nextval[4]拷贝nextval[next[4]]处的值，也就是-1

解释一下，按照next数组回退的话，下标为4处next[4]=0，会回退到下标为0处，而下标为0处next[0]=-1，会回退到下标为-1处，回退了两次。

但是如果应用改进的nextval数组，下标为4处next[4]=-1，直接回退到下标为-1处，只需要回退一次。

当遇到有大量连续重复元素的数组时，性能提升最为明显。

比如：

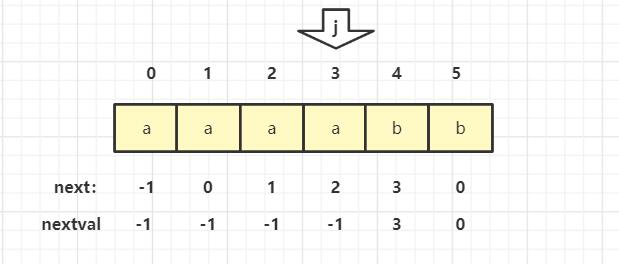
当 j=3 时，通过next数组回退需要先退到下标为2，再退到下标为1，在退到下标为0，最后退到下标为-1。

而通过nextval数组回退，一次就可以回退到下标为-1处。

//求nextval数组
    private static int[] nextval(String p, int[] nextval) {
        int right = 0, left = -1;  //left是前缀，right是后缀
        nextval[0] = -1;
        while (right < p.length()) {
            if (left == -1 || p.charAt(right) == p.charAt(left)) {
                left++;
                right++;         //多加了一次判断比较 nextval[right] 和 nextval[left]
                if (nextval[right] != nextval[left]) {
                    nextval[right] = left;
                } else {
                    nextval[right] = nextval[left];  //注意
                }
            } else {
                left = nextval[left];  //回退
            }
        }
        return nextval;
    }