分享一些自己对于<转向系统><传递路径分析>的理解

（只是一些个人理解，不涉及任何公司隐私问题，logo就懒得一个个去擦了）

(1)

(2)

(3)

(4)

(5)

(6)

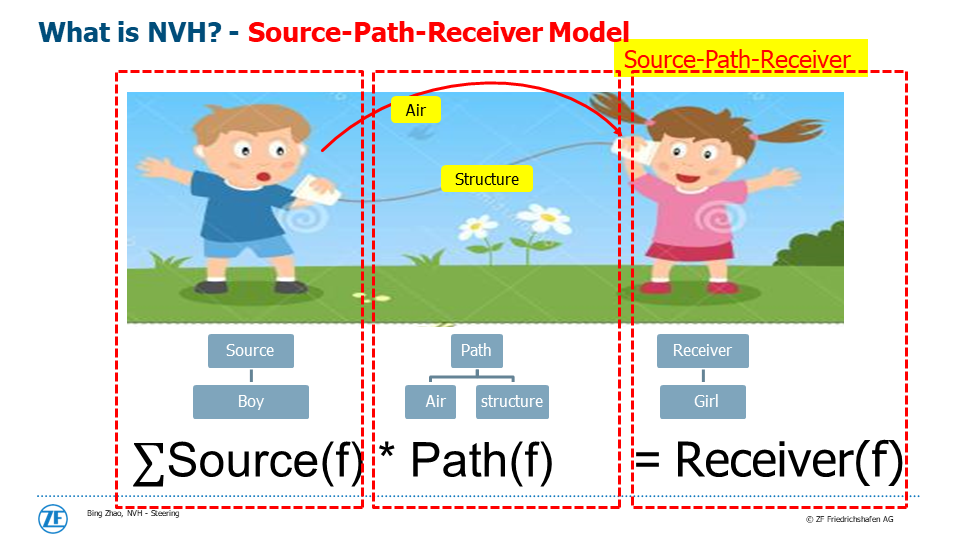
(7)

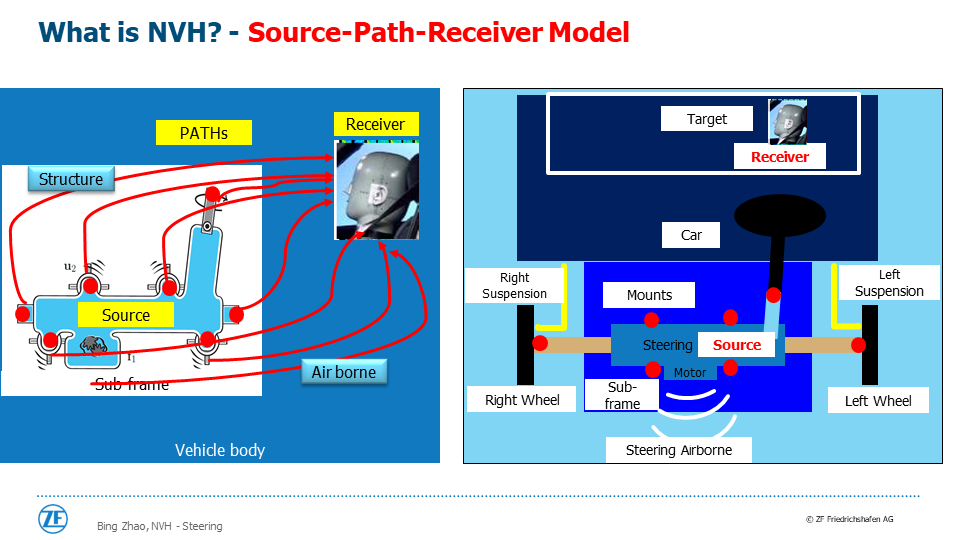
(8)

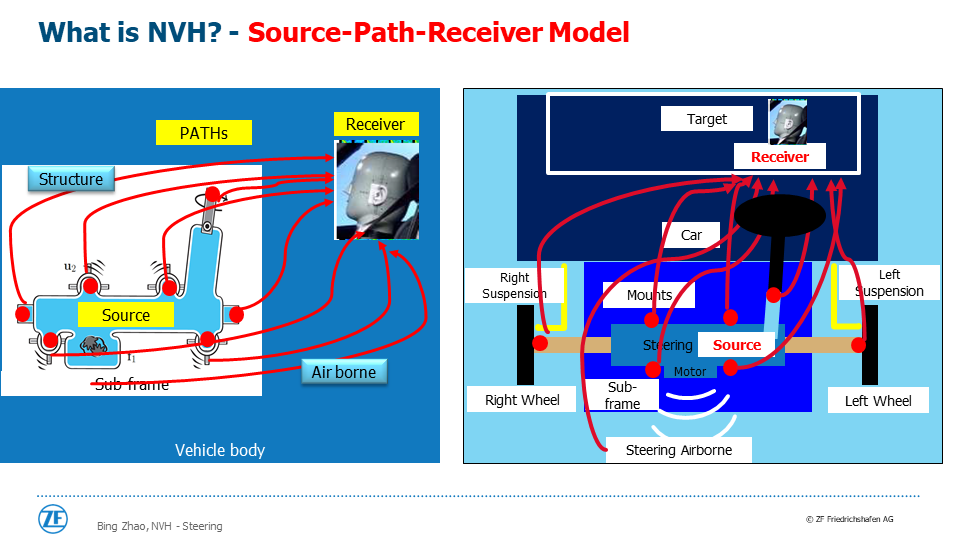
(9)

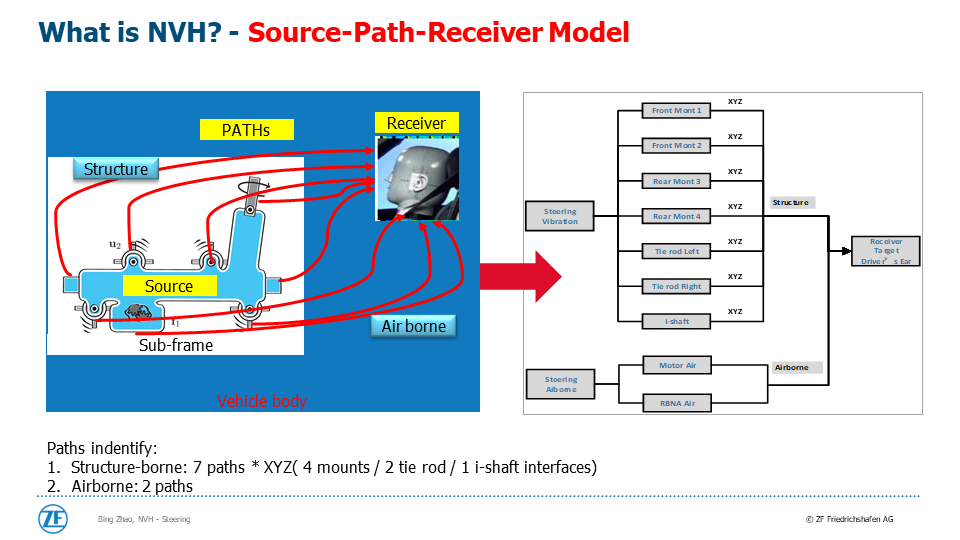
(10)

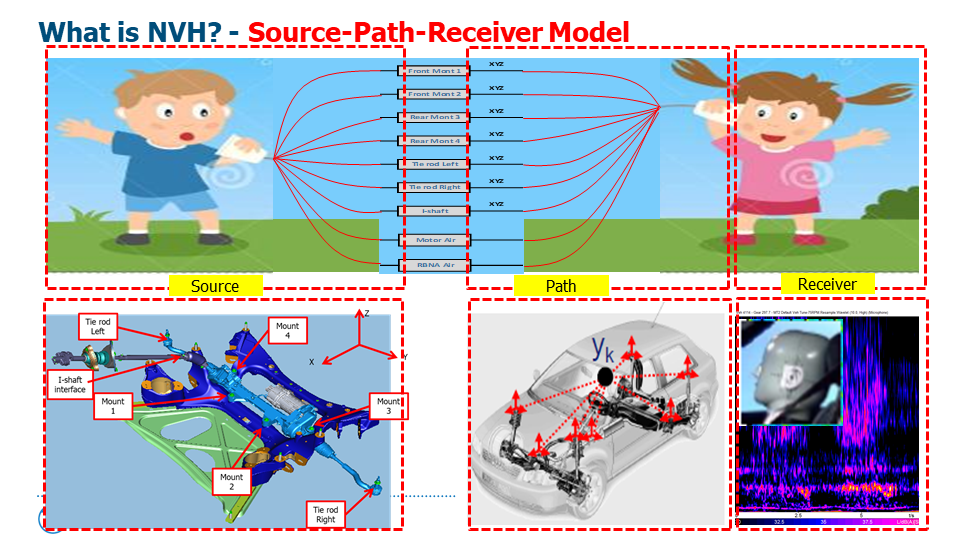
(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

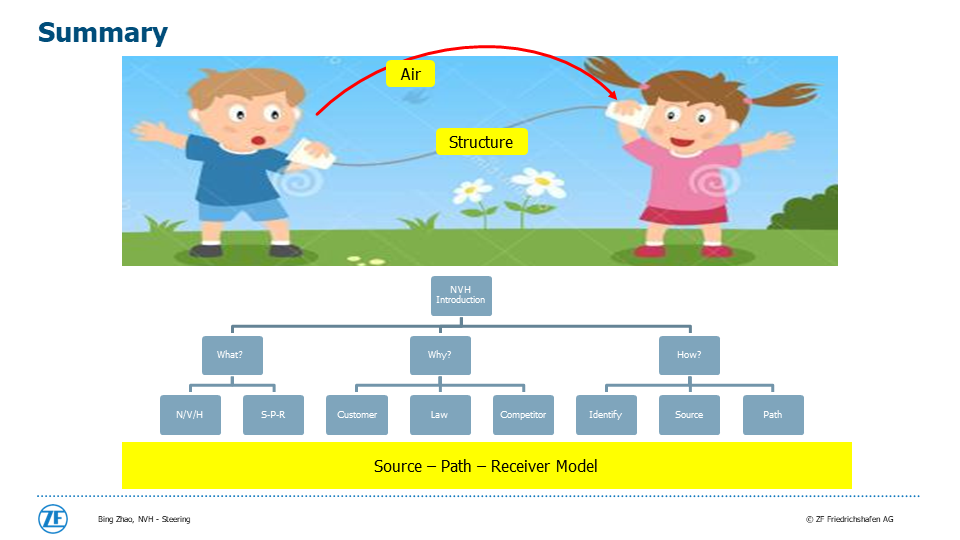
(20)

(21)

(22)

转向系统的传递路径分析（Transfer Path Analysis）入门的一些分享的更多相关文章

  1. 【论文笔记】Domain Adaptation via Transfer Component Analysis

    论文题目:<Domain Adaptation via Transfer Component Analysis> 论文作者:Sinno Jialin Pan, Ivor W. Tsang, ...

  2. HTTP监视器charles入门使用教程分享---http/s packet monitors---ubuntu installation

    charles --usage http://www.cnblogs.com/chenlogin/p/5849471.html 按照Charles的提示,PC打开 chls.pro/ssl下载得到一个 ...

  3. 用户路径分析（User Path Analysis）

    什么是用户路径? 用户路径即抽象用户在网站或APP中的访问路径.其可用桑基图展现,称为用户路径图. 什么是用户路径分析? 用户路径分析追踪用户从某个开始事件直到结束事件的行为路径,即对用户流向进行监测 ...

  4. 大堆文字不如几张图片-论信息传递的方式以NodeMCU入门为例

  5. 学习Objective-C入门教程（分享）

    原百度文库连接:http://wenku.baidu.com/view/6786064fe518964bcf847c63.html PS:需要原文档的可以留邮箱发送! (我叫雷锋,不要谢我) 学习Ob ...

  6. Neo4j入门博客分享

    Neo4j学习参考博客:https://www.cnblogs.com/ljhdo/p/5516793.html Neo4j Cypher查询语言详解 http://www.ttlsa.com/nos ...

  7. 实用教程！SPSSAU验证性因子分析思路总结

    验证性因子分析,是用于测量因子与测量项(量表题项)之间的对应关系是否与研究者预测保持一致的一种研究方法.尽管因子分析适合任何学科使用,但以社会科学居多. 目前有很多软件都可以非常便利地实现验证性因子分 ...

  8. servlet入门学习之工作原理解析

    从 Servlet 容器说起 要介绍 Servlet 必须要先把 Servlet 容器说清楚,Servlet 与 Servlet 容器的关系有点像枪和子弹的关系,枪是为子弹而生,而子弹又让枪有了杀伤力 ...

  9. Hadoop2-HDFS学习笔记之入门（不含YARN及MR的调度功能）

    架构 Hadoop整体由HDFS.YARN.MapReduce三大部分组成,推荐架构参考:https://www.cnblogs.com/zhjh256/p/10573684.html. 注:2.x的 ...

随机推荐

  1. 如何使用SQL的备份文件(.bak)恢复数据库

    出于很多情况,数据库只剩下.bak文件,想要恢复数据库,找了很多资料才知道可以这样!!!!! 个人觉得图片教程更有意义,请看步骤: 1.选中"数据库" 右击 选择"还原数 ...

  2. CSS写一个缺角的div和菱形

    <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...

  3. django 各项配置基本设置

    setting中一些设置例子 mysql数据库连接设置 DATABASES = { 'default': { 'ENGINE': 'django.db.backends.mysql', 'NAME': ...

  4. Java安全之ClassLoader

    Java安全之ClassLoader 类加载机制 Java中的源码.java后缀文件会在运行前被编译成.class后缀文件,文件内的字节码的本质就是一个字节数组 ,它有特定的复杂的内部格式,Java类 ...

  5. P4755-Beautiful Pair【笛卡尔树,线段树】

    正题 题目链接:https://www.luogu.com.cn/problem/P4755 题目大意 \(n\)个数字的一个序列,求有多少个点对\(i,j\)满足\(a_i\times a_j\le ...

  6. Redis对象

    概述 Redis并没有使用基础数据结构去实现键值数据库,而是基于数据结构封装了一个个对象. 类型和编码 由于Redis是键值数据库,所以每次存储数据时,至少包含两个对象,即K.V对应的对象.其数据结构 ...

  7. NOIP模拟69

    T1 石子游戏 大坑未补 T2 大鱼吃小鱼 解题思路 set+桶可以得到 60pts (code) 线段树上二分每一次优先递归右区间从右区间贪心选择,并且记录下更改过的值,在处理完答案之后再复原回去. ...

  8. 痞子衡嵌入式：我的三个小项目陆续上线恩智浦官方Github

    恍如眨眼间,痞子衡在飞思卡尔/恩智浦已经工作 8 年多了,前 5 年主要是在软件团队,最近 3 年在系统团队.所处团队不同,工作思维也不同,自从转到系统团队,开始跟客户打起交道,对待问题和解决问题的立 ...

  9. C++中string和char字符串的异同与使用方法

    C++中string和char声明字符串的异同和使用 string类 必须在头文件中包含<string> 隐藏了字符串的数组性质,可以像处理普通变量那样处理字符串 string类位于名称空 ...

  10. 8086的复位与启动 CPU执行指令的步骤

    东北大学-计算机硬件技术基础 CPU执行指令的步骤 取指令 Fetch 指令译码 Decode 执行指令 Execute 回写 Write-back 修改指令指针 取指令 将CS和IP的内容通过地址加 ...