【C语言】整型在内存中的存储

整型在内存中的存储

1.整型的归类

1. char
2. short
3. int
4. long

以上都分为有符号（signed）与无符号（unsigned）的类型

2.原码、反码和补码

2.1 定义

计算机在表示一个数字时，是采用二进制的方式，所以为了准确表示一个数的正负，每一个有符号数都将其最高位视作是符号位，最高位为0表示正数，最高位为1表示负数。我们接下来以有符号整型int的数字进行分析。

一个有符号整数由符号位+数值位组成，数值位是其最高位，分别以0/1表示正/负

对于正数来说，反码补码都与原码相同；

对于负数来说，符合以下3条规则：

1. 原码：将十进制数字直接翻译为二进制数
2. 反码：原码的符号位不变，其他位按位取反
3. 补码：反码+1

而对于整型来说，整型在内存中实际上是以补码的形式进行存储的。

2.2 补码的意义

有的同学可能就会问了，为什么计算机要发展出原码、反码、补码这么多种码呢？

这就与计算机对于整数的运算有关了。

CPU只有加法器，减法在运算时也会被视作一个数加另一个负数。考虑到整数的最高位是符号位，两个整数中若包含负数，以原码直接相加得到的数一定是不对的。所以问题就变成了如何使得运算简单而精确，既要处理符号位，又要只进行加法运算，达到以某一种二进制形式的“码”直接相加就能得到正确结果。

下面，我们以60+(-18)为例，分别用原码、反码、补码直接进行二进制的运算。

原码运算

  00000000 00000000 00000000 00111100（ 60的原码）
+ 10000000 00000000 00000000 00010010（-18的原码）
-------------------------------------------
  10000000 00000000 00000000 01001110（某个数的原码）

显然，得到了的原码转化为10进制是-78，并非正确答案42。

反码运算

  00000000 00000000 00000000 00111100（ 60的反码）
+ 11111111 11111111 11111111 11101101（-18的反码）
-------------------------------------------
 100000000 00000000 00000000 00101001
 截取后32位：
  00000000 00000000 00000000 00101001（某个数的反码）

显然，得到了的反码转化为10进制原码是41，并非正确答案42，但是只与正确答案相差（+1），于是，我们就想将负数的反码+1，即变成“补码”来进行运算，而又正数的补码是原码本身，这时候我们看看会怎么样呢？

补码运算

  00000000 00000000 00000000 00111100（ 60的补码）
+ 11111111 11111111 11111111 11101110（-18的反码）
-------------------------------------------
 100000000 00000000 00000000 00101010
 截取后32位：
  00000000 00000000 00000000 00101010（某个数的补码）

显然，得到了的补码转化为10进制原码是42，我们得到了正确结果。

2.3 结论

综上，我们发现，只要将两个整数使用补码进行运算，就不需要考虑它们的符号位了，将它们的所有位直接简单相加即可，就能得到正确的结果。

2.4* 负数二进制补码的快速转化

对于char类型整数，-1用二进制补码表示为

11111111

当我们已知一个负数的二进制补码时，用比这个数多一位的、最高位为1、其他位全0、这里应为9位的二进制数

100000000

直接减去-1的二进制补码得

00000001

得到的数就是十进制（-1）的绝对值，也就是1，只要加上负号，就能快速得到这个负数二进制补码的十进制原码。

原理十分简单，一个负数的原码加上补码 =原码+反码+1 = 所有二进制位全1再加1 = 多一位的、最高位为1、其他位全0

3. 大小端字节序

3.1 什么是大小端

在内存中，数据的大小端存储是在字节尺度上进行讨论的

大端存储模式：数据的低位保存在内存的高地址，数据的高位保存在内存的低地址

小端存储模式：数据的低位保存在内存的低地址，数据的高位保存在内存的高地址

3.2 为什么有大端和小端之分

在计算机系统中，我们通常是以字节为单位存储数据的，每个地址对应一个字节。

一个字节为8bit，但是在C语言中除了8bit的char之外，还有16bit的short，32bit的int。另外，对于位数大于8位的处理器，例如16位和32位的处理器，由于寄存器宽度大于一个字节，那么必然存在着如何将多个字节安排的问题。这边导致了大小端存储模式的诞生。

我们以int类型的数0x01ff4218为例（两个十六进制位即为1个字节），看一下在大小端下这4个字节分别是如何分配的

1. 大端存储模式
   
   
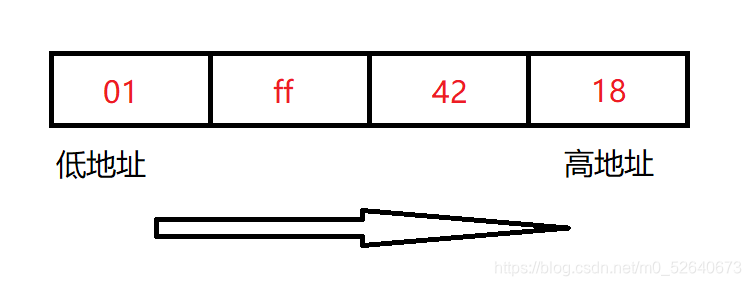
2. 小端存储模式
   
   

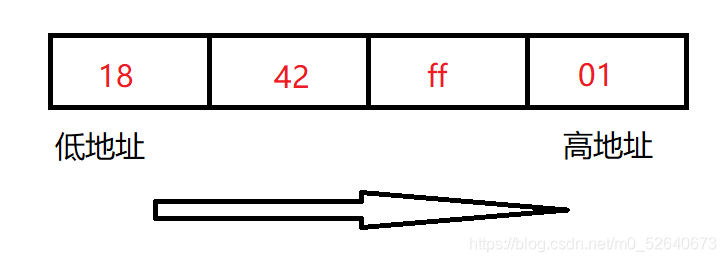
3.3 写一段代码来判断你的机器的大小端字节序

算法简单概括：截取4个字节大小的int整型的1个字节的低位。若机器为大端字节序，该字节存储0x00；若机器为小端字节序，该字节存储0x01；

#include<stdio.h>
//实现方法1
int check1()
{
	int i = 1;
	return *(char*)&i;
}

//实现方法2
int check2()
{
	union check
	{
		int i;
		char c;
	}ch = {1};
	return ch.c;
}

int main()
{
	int ret = check1();
	if (ret == 1)
	{
		printf("小端\n");
	}
	else
	{
		printf("大端\n");
	}
	return 0;
}

4.参考文献

1. C Primer Plus, 第六版, p494