Educational Codeforces Round 110 A-D 题解

  A. Fair Playoff

题目大意：有4个人进行比赛，第一个和第二个比，第三个和第四个比，之后各自的胜者再比，最开始每个人持有一个数字，每场比赛持有数字较大的选手会胜出，问最开始持有数字最大的两个选手能否会师决赛。

思路：如果持有数字最大的两个选手第一轮不能相遇就可以，否则不行。简单判断一下即可。

代码如下：

#include< bits/stdc++.h >
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

#define INF 0x3f3f3f3f
const double EPS = 1e-18;
const int MOD = 1e9 + 7;

int T, a[4];

void solve()
{
	if (a[0] >= a[2] && a[0] >= a[3] && a[1] >= a[2] && a[1] >= a[3])
		cout << "NO" << endl;
	else if (a[0] <= a[2] && a[0] <= a[3] && a[1] <= a[2] && a[1] <= a[3])
		cout << "NO" << endl;
	else
		cout << "YES" << endl;
}

int main()
{
	IOS;
	cin >> T;
	while (T--)
	{
		for (int i = 0; i < 4; i++)
			cin >> a[i];
		solve();
	}

	return 0;
}

B. Array Reodering

题目大意：有一个n个数组成的数组a，对于任意的ai,aj(1<=i<j<=n)，如果gcd(ai,2aj)>1，就说这对 i, j 是好的。a中的数字可以以任意顺序排列，求出a中是好的的 i, j 对的最大数量。

思路：显然如果ai为2的倍数，那么对于所有在( j, n ]之间的 j 都可以和 i 组成好的数对，为了使数量尽量大，应该尽量把2的倍数放在 a 中靠前的位置，先求出这部分结果。对于剩下的数，显然gcd(ai,2aj)=gcd(ai,aj)，ai, aj 的顺序不会影响结果，遍历剩余所有的 ai,aj 即可。

代码如下：

#include< bits/stdc++.h >
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

#define INF 0x3f3f3f3f
const double EPS = 1e-18;
const int MOD = 1e9 + 7;

int T, N, A[2001], B[10001];

int gcd(int a, int b)
{
	if (b == 0)
		return a;
	return gcd(b, a % b);
}

void solve()
{
	int res = 0;
	int b = N - 1;
	for (int i = 0; i < N; i++)
	{
		if (!(A[i] % 2))
		{
			res += b;
			b--;
		}
	}
	for (int i = 0; i < N - 1; i++)
	{
		if (A[i] % 2)
		{
			for (int j = i + 1; j < N; j++)
			{
				if (A[j] % 2)
				{
					if (gcd(A[i], A[j]) != 1)
						res++;
				}
			}
		}
	}
	cout << res << endl;
}

int main()
{
	IOS;
	cin >> T;
	while (T--)
	{
		cin >> N;
		for (int i = 0; i < N; i++)
			cin >> A[i];
		solve();
	}

	return 0;
}

C. Unstable String

题目大意：一个仅由‘0’, ‘1’, '?'组成的字符串S，'?'可以选择代表'1'也可以选择代表'0'，求这个字符串中所有可以变成没有任何连续的'1'或者'0'的字符串的连续子串的数量。

思路：一开始想了一个比较麻烦的DP：dp[i] 表示到si为止满足条件的连续子串的数量，q[i] 表示从si开始向前连续的 '?' 个数，len[i] 表示从从si开始向前能满足条件的串的最大长度，lst[i] 表示从从si开始向前能满足条件的串的最大长度。遍历一遍字符串根据情况分类更新上述4个数组，最后dp[strlen(S)-1]即为答案。

#include< bits/stdc++.h >
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

typedef long long ll;

#define INF 0x3f3f3f3f
const double EPS = 1e-18;
const int MOD = 1e9 + 7;

int T, N;
char str[200200];
ll dp[200200];
ll q[200200];
char lst[200200];
ll len[200200];

void solve()
{
	int s = strlen(str);
  //初始化
	dp[0] = 1;
	len[0] = 1;
	if (str[0] == '?')
	{
		q[0] = 1;
		lst[0] = '^';//如果第一个字符就是'?'，设str[-1]='^'
	}
	else
	{
		q[0] = 0;
		lst[0] = str[0];
	}
  
	for (int i = 1; i < s; i++)
	{
		if (str[i] == '?')//si为'?'
		{
			dp[i] = dp[i - 1] + len[i - 1] + 1;
			q[i] = q[i - 1] + 1;
			lst[i] = lst[i - 1];
			len[i] = len[i - 1] + 1;
		}
		else if (str[i] == '1')//si为'1'
		{
			q[i] = 0;
			lst[i] = '1';
			if (str[i - 1] == '0')
			{
				dp[i] = dp[i - 1] + len[i - 1] + 1;
				len[i] = len[i - 1] + 1;
			}
			else if (str[i - 1] == '1')
			{
				dp[i] = dp[i - 1] + 1;
				len[i] = 1;
			}
			else//si-1为'?'时还要根据前面连续'?'的个数即'?'链另一端的字符进行讨论
			{
				if (q[i - 1] % 2)
				{
					if (lst[i - 1] == '^' || lst[i - 1] == '1')
					{
						dp[i] = dp[i - 1] + len[i - 1] + 1;
						len[i] = len[i - 1] + 1;
					}
					else
					{
						dp[i] = dp[i - 1] + q[i - 1] + 1;
						len[i] = q[i - 1] + 1;
					}
				}
				else
				{
					if (lst[i - 1] == '^' || lst[i - 1] == '0')
					{
						dp[i] = dp[i - 1] + len[i - 1] + 1;
						len[i] = len[i - 1] + 1;
					}
					else
					{
						dp[i] = dp[i - 1] + q[i - 1] + 1;
						len[i] = q[i - 1] + 1;
					}
				}
			}
		}
		else//si为'0'
		{
			q[i] = 0;
			lst[i] = '0';
			if (str[i - 1] == '1')
			{
				dp[i] = dp[i - 1] + len[i - 1] + 1;
				len[i] = len[i - 1] + 1;
			}
			else if (str[i - 1] == '0')
			{
				dp[i] = dp[i - 1] + 1;
				len[i] = 1;
			}
			else//si-1为'?'时还要根据前面连续'?'的个数即'?'链另一端的字符进行讨论
			{
				if (q[i - 1] % 2)
				{
					if (lst[i - 1] == '^' || lst[i - 1] == '0')
					{
						dp[i] = dp[i - 1] + len[i - 1] + 1;
						len[i] = len[i - 1] + 1;
					}
					else
					{
						dp[i] = dp[i - 1] + q[i - 1] + 1;
						len[i] = q[i - 1] + 1;
					}
				}
				else
				{
					if (lst[i - 1] == '^' || lst[i - 1] == '1')
					{
						dp[i] = dp[i - 1] + len[i - 1] + 1;
						len[i] = len[i - 1] + 1;
					}
					else
					{
						dp[i] = dp[i - 1] + q[i - 1] + 1;
						len[i] = q[i - 1] + 1;
					}
				}
			}
		}
	}
	cout << dp[s - 1] << endl;
}

int main()
{
	IOS;
	cin >> T;
	while (T--)
	{
		cin >> str;
		solve();
	}

	return 0;
}

后来发现DP可以写得更简洁：

dp[i][0]：si加入后新增的可以'0'结尾的满足要求的字串数量。

dp[i][1]：si加入后新增的可以'1'结尾的满足要求的字串数量。

如果si=='0'，则dp[i][0]=dp[i-1][1]，si=='1'，则dp[i][1]=dp[i-1][0]，si=='?'，则dp[i][1]=dp[i-1][0]且dp[i][0]=dp[i-1][1]

更新完dp数组后再遍历一遍字符串，如果si=='0'，则ans+=dp[i][0]，si=='1'，则ans+=dp[i][1]，=='?'，则ans+=max(dp[i][0],dp[i][1])，最后ans即为答案。

#include< bits/stdc++.h >
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

typedef long long ll;

#define INF 0x3f3f3f3f
const double EPS = 1e-18;
const int MOD = 1e9 + 7;
const int maxn = 2e6 + 5;

int T;
ll dp[maxn][2];
char str[maxn];

void solve()
{
	ll ans = 0, n = strlen(str);
	for (int i = 0; i < n; i++)
		dp[i][0] = dp[i][1] = 0;
	if (str[0] == '0')
		dp[0][0] = 1;
	else if (str[0] == '1')
		dp[0][1] = 1;
	else
		dp[0][0] = dp[0][1] = 1;
	for (int i = 1; i < n; i++)
	{
		if (str[i] == '0')
			dp[i][0] = dp[i - 1][1] + 1;
		else if (str[i] == '1')
			dp[i][1] = dp[i - 1][0] + 1;
		else
		{
			dp[i][0] = dp[i - 1][1] + 1;
			dp[i][1] = dp[i - 1][0] + 1;
		}
	}
	for (int i = 0; i < n; i++)
	{
		if (str[i] == '0')
			ans += dp[i][0];
		else if (str[i] == '1')
			ans += dp[i][1];
		else
			ans += max(dp[i][1], dp[i][0]);
	}
	cout << ans << endl;
}

int main()
{
	IOS;
	cin >> T;
	while (T--)
	{
		cin >> str;
		solve();
	}

	return 0;
}

D. Playoff Tournament

题目大意：有2^k个队伍参加季后赛，每轮比赛按队伍序号从小到大每两队进行比赛。每轮也优先进行序号较小的两队之间的比赛，胜者进入下一轮，总共进行2^k - 1场比赛。

输入一串仅由‘0’, ‘1’, '?'组成的字符串来表示每场比赛的结果，每场比赛的赛果对应一个字符，如果是'0'则序号小的队伍晋级，是’1‘则序号大的队伍晋级，是’?'则两队都有可能晋级，之后输入q组询问，每个询问可以将字符串中的一个字符改为另一个‘0’, ‘1’, '?'中的字符，对每个询问输出可能夺冠的队伍总数。

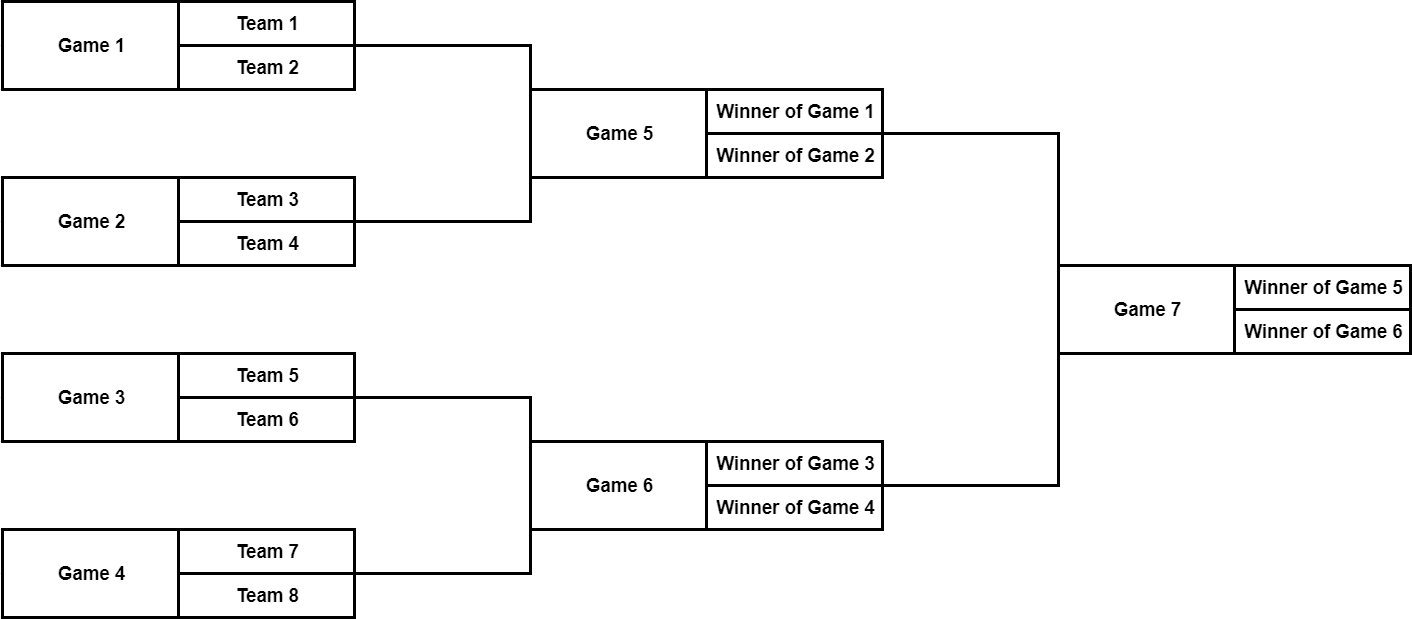
比赛流程

思路：维护每场比赛可能胜出的队伍总数d[i]，若参加第 i 场比赛的是从第 x 场比赛和第 y 场比赛胜出的队伍(不妨设x<y)，因为序号小的队伍对应的比赛场次在同一轮次中也一定较小，所以若第i场比赛对应的是’0‘，则d[i]=d[x]，若为'1'则d[i]=d[y]，若为’?'，则d[i]=d[x]+d[y]。d[2^k-1]即为答案。对于每个查询，在更新时只用更新该场比赛到决赛的晋级路径中的所有比赛即可。

代码如下：

#include< bits/stdc++.h >
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

#define INF 0x3f3f3f3f
const double EPS = 1e-18;
const int MOD = 1e9 + 7;
const int maxn = (2 << 18) + 1;

int n, dat[(1 << 20) + 1];
int K, N, Q;
int p;
char c;
string str;

void init(int _n)
{
	n = 1;
	while (n < _n)
		n *= 2;
	for (int i = 0; i < n * 2 - 1; i++)
		dat[i] = 1;
}

void update(int k)
{
	if (str[k] == '1')
		dat[k] = dat[k * 2 + 1];
	else if (str[k] == '0')
		dat[k] = dat[k * 2 + 2];
	else
		dat[k] = dat[k * 2 + 1] + dat[k * 2 + 2];
}

void solve()
{
	int r = N - p - 1;
	str[r] = c;
	update(r);
	while (r > 0)
	{
		r = (r - 1) / 2;
		update(r);
	}
	cout << dat[0] << endl;
}

int main()
{
	IOS;
	cin >> K;

	cin >> str;
	reverse(str.begin(), str.end());
	cin >> Q;

	N = 1 << K;//队伍数量
	init(N);
	for (int i = N - 2; i >= 0; i--)
		update(i);

	for (int i = 0; i < Q; i++)
	{
		cin >> p >> c;
		solve();
	}

	return 0;
}