jQurey判断下一项是否为指定项、下一项是否有指定项

jQurey判断下一项是否为指定项、下一项是否有指定项

---

此例子中，如果某个列表项没有二级列表，那么去掉它的展开、收起按钮。就是前边那个减号。

---

此时我们需要判断VOC综合治理技术这一项是否含有二级菜单，先来看一下代码结构

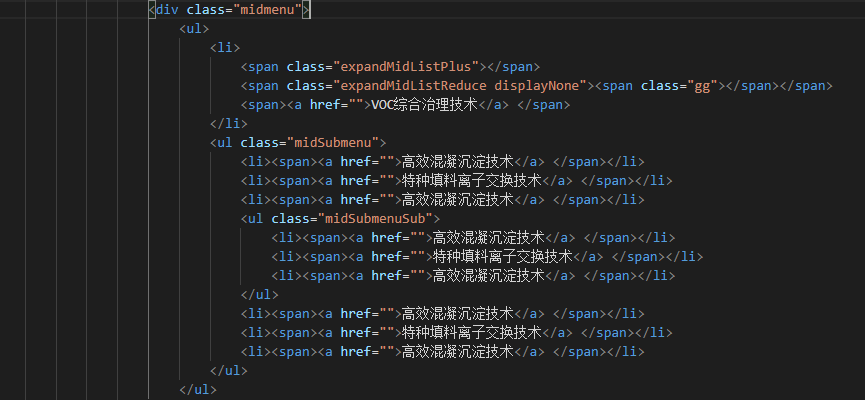
发现其父元素 li的下一项为midSubMenu

为子菜单，那么我们就可以对 midmenu ul li进行遍历

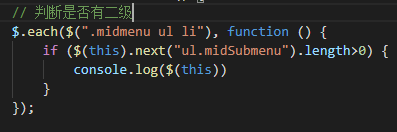
注意这里

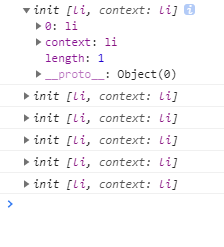
必须要写.length>0，不写看起来是个布尔值，但实际上不是的，jq如果找不到这个next()会自动将最后一个元素输出

结果如下：

只输出了有二级的项，如果我们需要没有二级的项，对if中的条件取反就可以拿到了，那么我们就可以对其类名进行修改或者增删，来达到我们的目的

需要注意的是，如果你不希望jq去寻找该类以下的所有li标签，那么应该在选择器中加入>

即：

这样只会寻找一级。