循环队列/顺序队列(C++)
队列(queue)是一种限定存取位置的线性变。他允许在表的一端插入,在另一端删除。这个和计算机调度策略中的先来先服务FCFS(First Come/First Served)是一样的。队列中可以插入的一端为队尾(rear),允许删除的一端称为队头(front)。

队列也分为两种,一种是用数组的存储表示,一种是基于链表的存储表示。
基于数组的存储表示的队列被称为顺序队列。其数据成员包括,一维数组elements用来存储数据,指针front和rear用来指示队尾队头的位置,maxSize是数组的最大长度。

从上边的图可以看出来,rear指针到指到数组最后一位时就不能继续往后添加元素,如果之前删除过元素,front指针前还有空闲的空间未被使用,造成空间的浪费。所以,使队列循环起来就可以使其最大限度的利用空间。
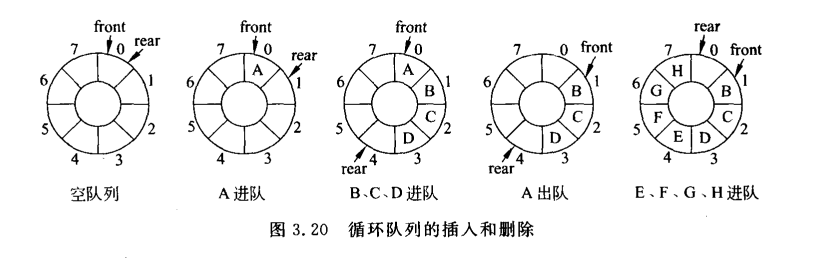
变成循环队列,为了避免越界,每次添加新元素时,尾指针需要加一后对堆长取余
即 rear = (rear+1)%maxSize;
删除元素也一样
front = (front+1)%maxSize;
为了区别于空队列,用(rear+1)%maxSize==front来判断是否队满,即队尾走到队头前一个位置即判定队满。再因为队尾所指的空间为最后一个元素的下一个位置,所以循环队列最多能存放maxSize-1个元素。
//queue.h
#ifndef _QUEUE_H
#define _QUEUE_H
#include<iostream>
using namespace std;
const int maxSize = 50;
template<class T>
class Queue
{
public:
Queue(){};
~Queue(){};
virtual bool EnQueue(const T& x) = 0;
virtual bool DeQueue(T& x) = 0;
virtual bool getFront(T& x) = 0;
virtual bool IsEmpty()const = 0;
virtual bool IsFull()const = 0;
virtual int getSize()const = 0;
};
#endif
//main.cpp
#include<assert.h>
#include"queue.h"
template<class T>
class SeqQueue;
template<class T>
ostream& operator<< (ostream& out, SeqQueue<T>& Q)//将友元函数声明在前可以避免其警告友元函数未声明
{
cout<<"front = "<<Q.front<<", rear = "<<Q.rear<<endl;
if(!Q.IsEmpty())
{
int i = Q.front;
while(i!=Q.rear)
{
cout<<Q.elements[i]<<" | ";
i = (++i)%maxSize;
}
}
return out; } template<class T>
class SeqQueue: public Queue<T>
{
private:
int rear, front;
T *elements;
int maxSize;
public:
SeqQueue(int sz=10);//构造函数
~SeqQueue(){delete[] elements;}//析构函数
bool EnQueue(const T& x);//入队列
bool DeQueue(T& x);//出队列
bool getFront(T& x);//找队头
bool IsEmpty()const{return (this->rear==this->front) ? true : false;}//判空
bool IsFull()const{return ((this->rear+1)%this->maxSize==this->front) ? true : false;}//判满
int getSize()const{return(this->rear-this->front+this->maxSize)%this->maxSize;}//得队长
friend ostream& operator<<<>(ostream& out, SeqQueue<T>& Q);
//void print();
};
/*template<class T>
void SeqQueue<T>::print()
{
if(!this->IsEmpty())
{
int i = this->front;
while(i!=this->rear)
{
cout<<this->elements[i]<<" | ";
i = (++i)/this->maxSize;
}
}
}*/
template<class T>
bool SeqQueue<T>::EnQueue(const T& x)
{
if(!this->IsFull())
{
this->elements[this->rear] = x;
this->rear = (this->rear+1)%this->maxSize;
return true;
}
return false;
}
template<class T>
bool SeqQueue<T>::DeQueue(T& x)
{
if(!this->IsEmpty())
{
x = this->elements[this->front];
this->front = (this->front+1)%this->maxSize;
return true;
}
return false;
}
template<class T>
bool SeqQueue<T>::getFront(T& x)
{
if(!this->IsEmpty())
{
x = this->elements[this->front];
return true;
}
return false;
}
template<class T>
SeqQueue<T>::SeqQueue(int sz):front(0),rear(0),maxSize(sz)
{
this->elements = new T[maxSize];
assert(this->elements!=NULL);
}
int main()
{
SeqQueue<int> Q(7);
for(int i=7; i>0; --i)
Q.EnQueue(i);
cout<<Q<<endl;//声明友元函数并重载输出运算符<<就可以用cout直接输出对象
int q = 0;
for(int i=3; i>=0; --i)
Q.DeQueue(q);
cout<<Q<<endl;
cout<<"Size = "<<Q.getSize()<<endl;
return 0;
}
运行结果
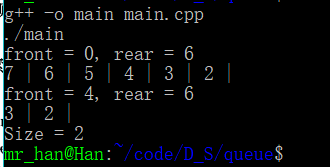
循环队列/顺序队列(C++)的更多相关文章
- Javascript数据结构与算法--队列(顺序队列、优先队列、循环队列)的实现与用法
前言 队列和栈非常类似,前面已经讲过了栈的实现与用法,现在我们来说说队列. 队列介绍 队列遵循FIFO(First In First Out,先进先出)原则的一组有序的项. 队列是一种特殊的线性表,特 ...
- javascript实现数据结构与算法系列:队列 -- 链队列和循环队列实现及示例
1 队列的基本概念 队列(Queue):也是运算受限的线性表.是一种先进先出(First In First Out ,简称FIFO)的线性表.只允许在表的一端进行插入,而在另一端进行删除. 队首(fr ...
- 数据结构Java实现07----队列:顺序队列&顺序循环队列、链式队列、顺序优先队列
一.队列的概念: 队列(简称作队,Queue)也是一种特殊的线性表,队列的数据元素以及数据元素间的逻辑关系和线性表完全相同,其差别是线性表允许在任意位置插入和删除,而队列只允许在其一端进行插入操作在其 ...
- 数据结构----队列:顺序队列&顺序循环队列、链式队列、顺序优先队列
一.队列的概念: 队列(简称作队,Queue)也是一种特殊的线性表,队列的数据元素以及数据元素间的逻辑关系和线性表完全相同,其差别是线性表允许在任意位置插入和删除,而队列只允许在其一端进行插入操作在其 ...
- 用数组实现队列(顺序队列&循环队列)
用数组实现队列(顺序队列&循环队列) 顺序队列 ️ 队列(先进先出) 几个问题: 队列方法:入队.出队 队列的存储:即队首队尾两个指针, 扩容:如果队列容量不够了,应该扩容,如果队尾没有位置了 ...
- C语言顺序队列
顺序队列是一种只能在一头进和另一头出的数据结构,所以结构体里设2个指针分别指向头部和尾部,用数组来存储数据. #define MAXSIZE 1024 typedef int elemtype; ty ...
- 总结:JavaScript异步、事件循环与消息队列、微任务与宏任务
本人正在努力学习前端,内容仅供参考.由于各种原因(不喜欢博客园的UI),大家可以移步我的github阅读体验更佳:传送门,喜欢就点个star咯,或者我的博客:https://blog.tangzhen ...
- 数据结构 - 顺序队列的实行(C语言)
数据结构-顺序队列的实现 1 顺序队列的定义 线性表有顺序存储和链式存储,队列作为一种特殊的线性表,也同样存在这两种存储方式.我们先来看队列的顺序存储结构. 队列的顺序储存结构:用数组存储队列,为了避 ...
- 数据结构之顺序队列(C实现)
一.队列是什么 队列是一种可以实现“先进先出”的存储结构. 队列通常可以分为两种类型: 一.顺序队列,采用顺序存储,当长度确定时使用. 顺序队列又有两种情况: ①使用数组存储队列的称为静态顺序队列. ...
随机推荐
- python进阶(22)pydantic--数据类型校验
pydantic库的作用 pydantic库是一种常用的用于数据接口schema定义与检查的库. Pydantic 在运行时强制执行类型提示,并在数据无效时提供用户友好的错误信息. pydantic安 ...
- 羽夏看Win系统内核——SourceInsight 配置 WRK
写在前面 此系列是本人一个字一个字码出来的,包括示例和实验截图.由于系统内核的复杂性,故可能有错误或者不全面的地方,如有错误,欢迎批评指正,本教程将会长期更新. 如有好的建议,欢迎反馈.码字不易, ...
- K8S 部署 SpringBoot 项目(一篇够用)
现在比较多的互联网公司都在尝试将微服务迁到云上,这样的能够通过一些成熟的云容器管理平台更为方便地管理微服务集群,从而提高微服务的稳定性,同时也能较好地提升团队开发效率. 但是迁云存在一定的技术难点,今 ...
- Spring IOC&DI 控制反转和依赖注入
控制反转(Inversion of Control,缩写为IOC),它是把你设计好的对象交给spring控制,而不再需要你去手动 new Object(); 网上对于IOC的解释很多,对程序员而言,大 ...
- 彻底搞懂Spring状态机原理,实现订单与物流解耦
本文节选自<设计模式就该这样学> 1 状态模式的UML类图 状态模式的UML类图如下图所示. 2 使用状态模式实现登录状态自由切换 当我们在社区阅读文章时,如果觉得文章写得很好,我们就会评 ...
- python实现图片色素的数值运算(加减乘除)和逻辑运算(与或非异或)
目录: (一)数值运算(加减乘除) (二)逻辑运算(与或非异或) 正文: (一)数值运算(加减乘除) opencv自带图片色素的处理函数------相加:add() 相减:subtract() ...
- 对于VS2013使控制台暂停的方法
#include<stdio.h>int main(){ int year, leap; printf("enter year:"); scanf_s ...
- [luogu4607]反回文串
参考ARC064F 令$h(n)=\begin{cases}n(n为奇数)\\\frac{n}{2}(n为偶数)\end{cases}$,$f(n)$定义与ARC064F相同,答案即$\sum_{d| ...
- [nowcoder5667H]Happy Triangle
可以发现合法的答案有两种可能: 1.询问的$x$即为最大值(或之一),那么只需要找到x前两个数并判断即可 2.询问的$x$不是最大值,那么就要保证另外两边之差小于$x$,维护后缀中$的前驱k-k的前驱 ...
- SpringCloud升级之路2020.0.x版-41. SpringCloudGateway 基本流程讲解(1)
本系列代码地址:https://github.com/JoJoTec/spring-cloud-parent 接下来,将进入我们升级之路的又一大模块,即网关模块.网关模块我们废弃了已经进入维护状态的 ...
