Python计算期权隐含波动率

更多精彩内容，欢迎关注公众号：数量技术宅，也可添加技术宅个人微信号：sljsz01，与我交流。

Black-Scholes 将期权价格描述为标的价格、行权价、无风险利率、到期时间和波动性的函数。

V=BS(S,K,r,T,σ)

在本文中，我们使用的波动率值是对未来已实现价格波动率的估计。

鉴于股票价格、行权价、无风险利率和到期时间都是已知且容易找到的，我们实际上可以将市场上的期权价格视为 σ 的函数。

V=BS(σ)

期权的价格在 σ 中单调增加，这意味着随着波动性的增加，期权的价值也会增加，如下图所示。

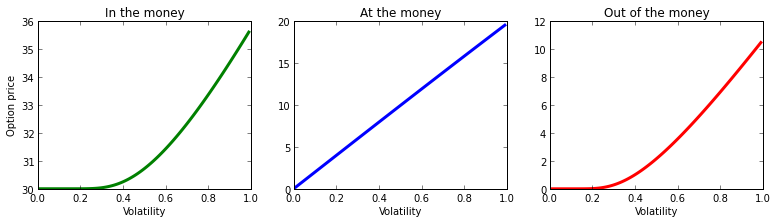
当价格等于期权行权价时，其结果是线性的（中间图）。而当行权价高于或低于当前价格时（左右图），波动性的增加也会对期权价格产生积极影响。

寻找市场隐含波动率

以下是 GOOG 的看涨期权报价，其行使价为 585.00，到期日为 2014 年 10 月 18 日。最后交易价格为 17.50 美元。

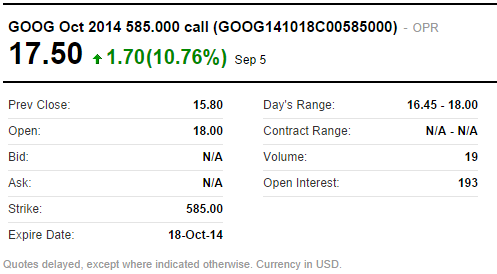
到目前为止，我们知道我们的期权价格 V 、我们的行权价 K 和到期时间 T，上述数据是从雅虎财经获得的。GOOG 的交易价格为 586.08 美元，现在我们知道了S，唯一缺少的是无风险利率 r ，我们可以通过找到接近我们的期权到期时到期的国库券利率来近似无风险利率。4 周利率目前为 0.02% ，我们可以把这个数值当作是r。

从目前收集到的数据中，我们可以看到：

V=BS(S,K,r,T,σ)

$17.50=BS(586.08,585.00,0.0002,0.10958....,σ)

现在我们有一个方程，其中只有一个未知变量，即波动率。然而，我们无法重新排列 Black-Scholes 公式来求解波动性。但是，我们知道价格相对于波动率是单调增加的，因此我们可以尝试猜测波动率是多少，然后找出该期权的价值。如果该值太高，我们降低我们的猜测，反之亦然，并重复直到我们找到 σ 的值，使我们的期权价格足够接近市场价格。

虽然上述方法可行，但它相当不精确。我们可以做的是使用求根方法，如二分法或牛顿法。

牛顿法

牛顿法是一种寻找函数根的提高近似值的方法。通过隐含波动率，我们试图找出使我们的期权价格尽可能接近 8.50 美元的 σ 值。

如果我们有一个函数 f(x) 及其导数 f'(x)，我们可以从初始猜测开始，然后通过以下方式通过更新的猜测不断迭代它：

Xn+1=Xn−f(Xn)/f′(Xn)

为了找到隐含波动率，我们想要找到的根是我们的 Black-Scholes 价格在一定程度上与市场价格相匹配的。我们可以这样表达：

|Vmarket−Vmodel|>=ϵ

其中 ϵ 是精度水平，Vmarket 是期权的市场价格。

这里，我们的 f(x) 函数是期权定价的 Black-Scholes 方程：

Vmodel=f(x)=BS(σ)

正如您可能猜到的，价格相对于波动率的导数是 vega，这将是我们的 f'(x) 函数。

Python实现隐含波动率计算

那么让我们在python中实现牛顿的方法：

def find_vol(target_value, call_put, S, K, T, r):
    MAX_ITERATIONS = 100
    PRECISION = 1.0e-5

    sigma = 0.5
    for i in xrange(0, MAX_ITERATIONS):
        price = bs_price(call_put, S, K, T, r, sigma)
        vega = bs_vega(call_put, S, K, T, r, sigma)

        price = price
        diff = target_value - price  # 我们的根

        print i, sigma, diff

        if (abs(diff) < PRECISION):
            return sigma
        sigma = sigma + diff/vega # f(x) / f'(x)

    # 未找到值，返回迄今为止的最佳猜测
    return sigma

这里，我们将精度设置为 1e-5 (0.00001)，并且我们不会执行超过 100 次的猜测。

我们还需要两个计算Black-Scholes公式的函数，bs_price 和 bs_vega：

n = norm.pdf
N = norm.cdf

def bs_price(cp_flag,S,K,T,r,v,q=0.0):
    d1 = (log(S/K)+(r+v*v/2.)*T)/(v*sqrt(T))
    d2 = d1-v*sqrt(T)
    if cp_flag == 'c':
        price = S*exp(-q*T)*N(d1)-K*exp(-r*T)*N(d2)
    else:
        price = K*exp(-r*T)*N(-d2)-S*exp(-q*T)*N(-d1)
    return price

def bs_vega(cp_flag,S,K,T,r,v,q=0.0):
    d1 = (log(S/K)+(r+v*v/2.)*T)/(v*sqrt(T))
    return S * sqrt(T)*n(d1)

让我们尝试找出上面报价的隐含波动率：

V_market = 17.5
K = 585
T = (datetime.date(2014,10,18) - datetime.date(2014,9,8)).days / 365.
S = 586.08
r = 0.0002
cp = 'c' # 看涨期权

implied_vol = find_vol(V_market, cp, S, K, T, r)

print 'Implied vol: %.2f%%' % (implied_vol * 100)

print 'Market price = %.2f' % V_market
print 'Model price = %.2f' % bs_price(cp, S, K, T, r, implied_vol)

运行Python代码，得到结果：

Implied vol: 21.92%
Market price = 17.50
Model price = 17.50

到这里，我们已经成功计算了上述期权的隐含波动率。 2014 年 10 月 18 日到期的 585 美元看涨期权的隐含波动率为 21.92%。

往期干货分享推荐阅读

通过深度学习股价截面数据分析和预测股票价格

Omega System Trading and Development Club内部分享策略Easylanguage源码

一个真实数据集的完整机器学习解决方案（下）

一个真实数据集的完整机器学习解决方案（上）

如何使用交易开拓者（TB）开发数字货币策略

股指期货高频数据机器学习预测

如何使用TradingView（TV）回测数字货币交易策略

如何投资股票型基金？什么时间买？买什么？

【数量技术宅|量化投资策略系列分享】基于指数移动平均的股指期货交易策略

AMA指标原作者Perry Kaufman 100+套交易策略源码分享

【数量技术宅 | 期权系列分享】期权策略的“独孤九剑”

【数量技术宅|金融数据系列分享】套利策略的价差序列计算，恐怕没有你想的那么简单

【数量技术宅|量化投资策略系列分享】成熟交易者期货持仓跟随策略

如何获取免费的数字货币历史数据

【数量技术宅|量化投资策略系列分享】多周期共振交易策略

【数量技术宅|金融数据分析系列分享】为什么中证500（IC）是最适合长期做多的指数

商品现货数据不好拿？商品季节性难跟踪？一键解决没烦恼的Python爬虫分享

【数量技术宅|金融数据分析系列分享】如何正确抄底商品期货、大宗商品

【数量技术宅|量化投资策略系列分享】股指期货IF分钟波动率统计策略

【数量技术宅 | Python爬虫系列分享】实时监控股市重大公告的Python爬虫