信息论估计工具jidt基本使用

JIDT基本介绍

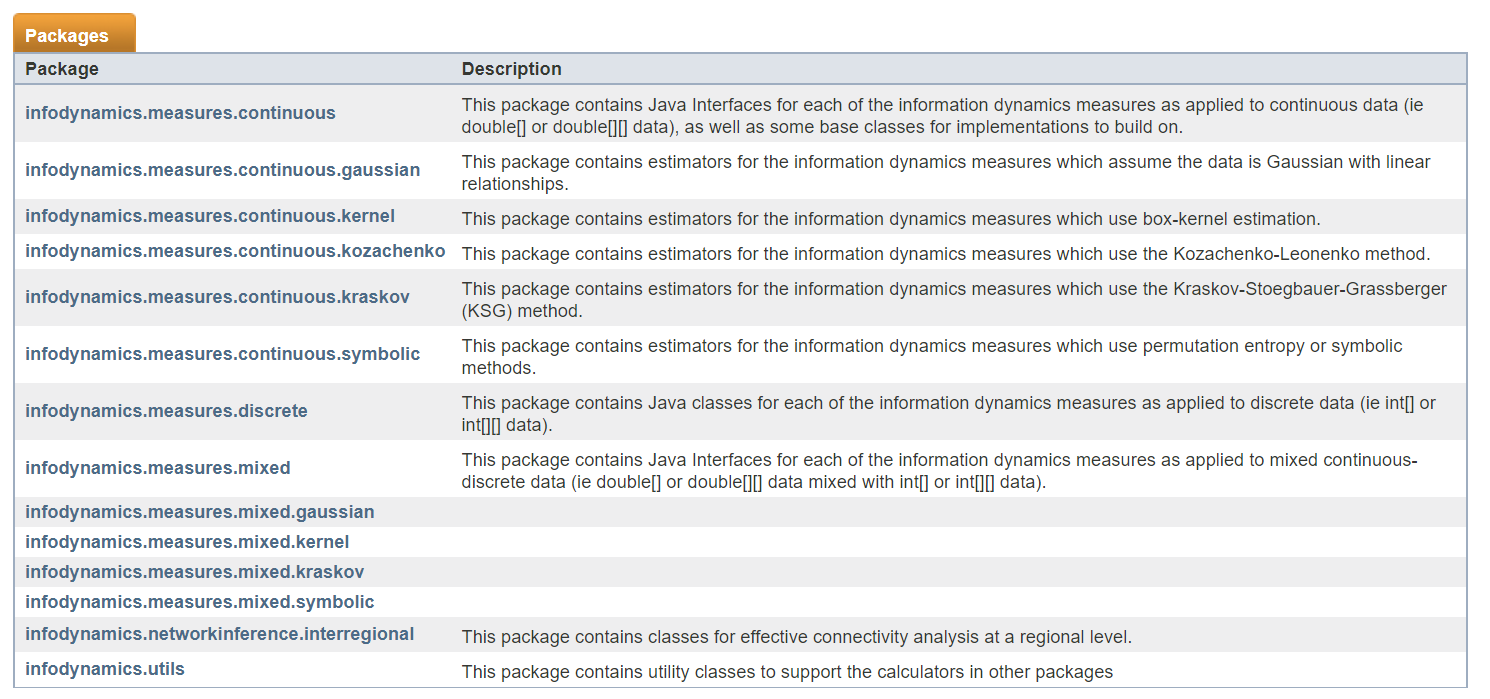
• JIDT是 Java Information Dynamics Toolkit的简称，用于研究复杂系统中信息论相关度量的计算，它是一个基于java的开源工具库，也可以在Matlab、Octave、Python、R、Julia和Clojure中使用；
• JIDT提供了如下计算工具：
  • 信息熵、互信息、转移熵
  • 条件互信息、条件转移熵
  • 多变量互信息和多变量转移熵
  • 信息存储
• JIDT同时支持离散型数据和连续型数据
• JIDT提供多种估计算子

主页：https://github.com/jlizier/jidt

安装

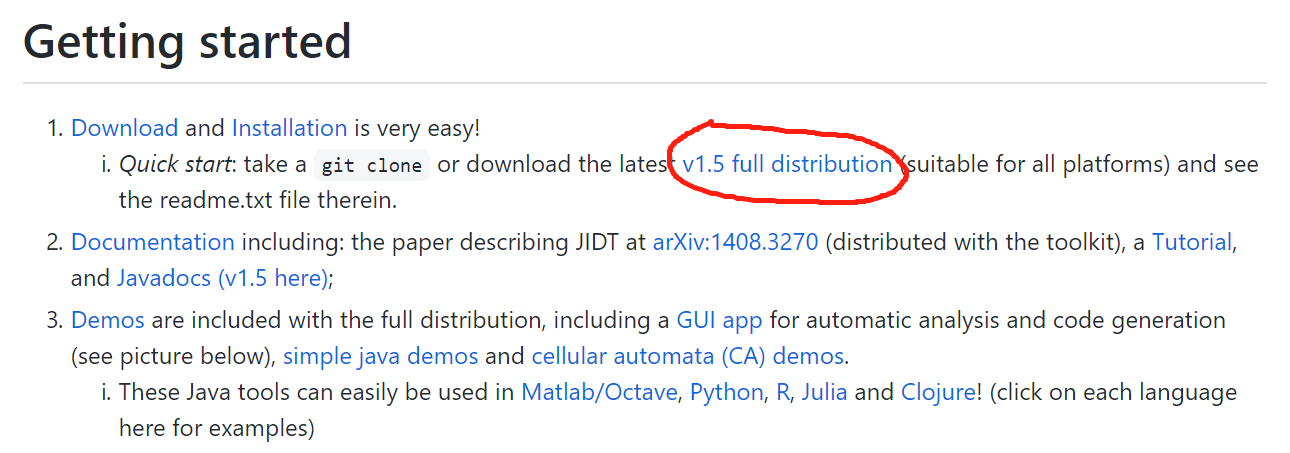
• 第一步：下载编译好的版本，图中的v1.5 full distribution，然后解压放到合适的目录，如~/software/infodynamics，我们只需要里面的infodynamics.jar文件。

• 第二步：熟悉Java的同学应该知道这个jar文件是个什么东东，这就是所有信息论度量计算所需要的函数哈，所以现在需要安装配置Java环境，这里不再赘述。

• 第三步：由于需要在python环境中使用java计算，所以需要安装jpype，安装命令：pip install jpype1

配置好环境之后，在使用jidt之前加入如下一段代码：

import jpype
from jpype import *

try:
    jarLocation = "~/software/infodynamics/infodynamics.jar"
    jpype.startJVM(jpype.getDefaultJVMPath(), "-ea", "-Djava.class.path=" + jarLocation)
except:
    print("JVM  has already started !")

注： 需要把jarLocation换成自己的路径！

接下来就能够调用jidt中各种封装好的信息论估计算子了：

转移熵估计

转移熵估计作者提供了多种估计方法：

• TransferEntropyCalculator
• TransferEntropyCalculatorDiscrete
• TransferEntropyCalculatorGaussian
• TransferEntropyCalculatorKernel
• TransferEntropyCalculatorKernelPlain
• TransferEntropyCalculatorKernelPlainIterators
• TransferEntropyCalculatorKernelSeparate
• TransferEntropyCalculatorKraskov
• TransferEntropyCalculatorMultiVariate
• TransferEntropyCalculatorMultiVariateGaussian
• TransferEntropyCalculatorMultiVariateKernel
• TransferEntropyCalculatorMultiVariateKraskov
• TransferEntropyCalculatorMultiVariateSingleObservationsKernel
• TransferEntropyCalculatorMultiVariateViaCondMutualInfo
• TransferEntropyCalculatorSymbolic
• TransferEntropyCalculatorViaCondMutualInfo
• TransferEntropyCommon
• TransferEntropyKernelCounts

例：TransferEntropyCalculatorMultiVariateKraskov

我们以这个多变量转移熵的ksg估计算子为例来介绍如何使用jidt估计转移熵，首先使用如下代码打开JVM：

import jpype
from jpype import *

try:
    jarLocation = "~/software/infodynamics/infodynamics.jar"
    jpype.startJVM(jpype.getDefaultJVMPath(), "-ea", "-Djava.class.path=" + jarLocation)
except:
    print("JVM  has already started !")

然后安装如下方式，实例化一个计算子：

calcClass = JPackage(
    "infodynamics.measures.continuous.kraskov"
).TransferEntropyCalculatorMultiVariateKraskov
calc = calcClass()

对于其他的估计子，只须替换上面的相应名称即可，具体名称可以查看官方文档，然后我们就可以用这个calc

来搞一些具体计算了哈，先生成一些数据：

start, end = "1996", "1996"
columns = ["Electric_field"]
x = data.loc[start:end, columns].interpolate().values
y = data.loc[start:end, ["Dst"]].interpolate().values

fig, axs = plt.subplots(2, 1, figsize=(6, 4))
axs[0].plot(x, label="Electric_field", color="blue")
axs[0].legend()
axs[1].plot(y, label="Dst", color="red")
axs[1].legend()
plt.show()

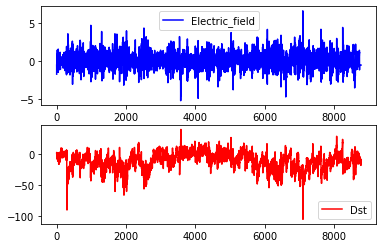
这里使用的是1996年卫星观测的行星际电场数据和磁暴指数Dst数据，注意x和y都是二维矩阵：x.shape=(8784,1); y.shape=(8784,1)

然后设置一些calc的参数：

calc.setProperty("k_HISTORY", str(k_HISTORY))
calc.setProperty("k_TAU", str(k_TAU))
calc.setProperty("l_HISTORY", str(l_HISTORY))
calc.setProperty("l_TAU", str(l_TAU))
calc.setProperty("DELAY", str(DELAY))

注： 这里的DELAY是平常计算转移熵所设置的延迟\(\tau\)

设置好参数之后就可以直接计算了：

m,n = 1,1
calc.initialise(m,n)
calc.setObservations(
    JArray(JDouble, 2)(x), JArray(JDouble, 2)(y)
)

result = calc.computeAverageLocalOfObservations()

由于x和y都是一维变量，所以初始化的时候m和n都设置成1即可，JArray(JDouble, 2)(x)是通过jpype将python中的矩阵转化成java中的数据类型，result即为计算出的转移熵。

如需评估所计算转移熵的重要性，只需要进一步计算p值即可：

sig_num = 100
measDist = calc.computeSignificance(self.sig_num)
mean = (measDist.getMeanOfDistribution(),)
std = (measDist.getStdOfDistribution(),)
pVal = measDist.pValue

这里使用的是替代数据检验法，生成sig_num条与x尺寸相同的随机数据，然后计算到y的转移熵，计算sig_num个统计值的均值、标准差以及相应的p值即可评估上面计算得到的result是否可信。

为避免每次都需要这么设置，可以将上述过程封装成一个类，具体如下：

import os, sys
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pathlib import Path

Path.ls = lambda x: list(x.iterdir())
from tqdm import tqdm

"""
多变量转移熵计算
"""
import os, sys
import numpy as np
import pandas as pd
import jpype
from jpype import *

# mUtils = JPackage("infodynamics.utils").MatrixUtils

class TransferEntropyCalculatorMultiVariateKraskov:

    """
    Description:

    """

    def __init__(
        self,
        source=None,
        destination=None,
        sourceDimensions=2,
        destDimensions=2,
        k_HISTORY=1,
        k_TAU=1,
        l_HISTORY=1,
        l_TAU=1,
        DELAY=1,
        k=4,
        NOISE_LEVEL_TO_ADD=1e-8,
        ALG_NUM=1,
        cal_sig=False,
        sig_num=100,
    ):

        self.source = source
        self.destination = destination
        self.sourceDimensions = sourceDimensions
        self.destDimensions = destDimensions
        self.k_HISTORY = k_HISTORY
        self.k_TAU = k_TAU
        self.l_HISTORY = l_HISTORY
        self.l_TAU = l_TAU
        self.DELAY = DELAY
        self.k = k
        self.cal_sig = cal_sig
        self.sig_num = sig_num
        self.NOISE_LEVEL_TO_ADD = NOISE_LEVEL_TO_ADD
        self.ALG_NUM = ALG_NUM

    def __call__(self, source, destination, tau, m=1, n=1):

        self.source = source
        self.destination = destination
        self.sourceDimensions = np.min(source.shape)
        self.destDimensions = np.min(destination.shape)
        self.DELAY = tau

        calcClass = JPackage(
            "infodynamics.measures.continuous.kraskov"
        ).TransferEntropyCalculatorMultiVariateKraskov
        calc = calcClass()

        calc.setProperty("sourceDimensions", str(self.sourceDimensions))
        calc.setProperty("destDimensions", str(self.destDimensions))
        calc.setProperty("k_HISTORY", str(self.k_HISTORY))
        calc.setProperty("k_TAU", str(self.k_TAU))
        calc.setProperty("l_HISTORY", str(self.l_HISTORY))
        calc.setProperty("l_TAU", str(self.l_TAU))
        calc.setProperty("DELAY", str(self.DELAY))
        calc.setProperty("k", str(self.k))
        calc.setProperty("NOISE_LEVEL_TO_ADD", str(self.NOISE_LEVEL_TO_ADD))
        calc.setProperty("ALG_NUM", str(self.ALG_NUM))

        calc.initialise(m,n)
        self.calc = calc
        self.calc.setObservations(
            JArray(JDouble, 2)(source), JArray(JDouble, 2)(destination)
        )

        result = self.calc.computeAverageLocalOfObservations()
        if not self.cal_sig:
            return result
        else:
            measDist = self.calc.computeSignificance(self.sig_num)
            mean = (measDist.getMeanOfDistribution(),)
            std = (measDist.getStdOfDistribution(),)
            pVal = measDist.pValue
            return result, [mean, std, pVal]    

# estimator_ksg = TransferEntropyCalculatorMultiVariateKraskov()

然后计算就很简单了：

# 实例化一个估计子
estimator_ksg = TransferEntropyCalculatorMultiVariateKraskov()

# 生成测试数据
start, end = "1996", "1996"
columns = ["Electric_field"]
x = data.loc[start:end, columns].interpolate().values
y = data.loc[start:end, ["Dst"]].interpolate().values

fig, axs = plt.subplots(2, 1, figsize=(6, 4))
axs[0].plot(x, label="Electric_field", color="blue")
axs[0].legend()
axs[1].plot(y, label="Dst", color="red")
axs[1].legend()
plt.show()

# 计算转移熵结果，并绘制图像
result = []
taus = 168
for tau in tqdm(range(taus)):
    result.append(estimator_ksg(source=x, destination=y, tau=tau))

plt.figure(figsize=(8, 3))
plt.plot(range(taus), result)

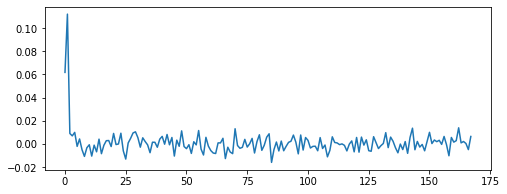
大概几秒之后就计算完毕了，速度还是非常可以的，计算结果如下：

今天的部分到这里就结束了，后期作者会在介绍一下其他方法和信息论度量的计算，并将完整代码总结发布到github上面，敬请关注。