【数据结构与算法Python版学习笔记】图——骑士周游问题 深度优先搜索

骑士周游问题

概念

• 在一个国际象棋棋盘上， 一个棋子“马”（骑士） ， 按照“马走日”的规则， 从一个格子出发， 要走遍所有棋盘格恰好一次。把一个这样的走棋序列称为一次“周游”

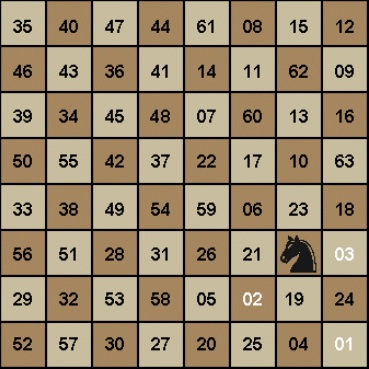
• 在8×8的国际象棋棋盘上， 合格的“周游”数量有1.305×1035这么多， 走棋过程中失败的周游就更多了
• 采用图搜索算法， 是解决骑士周游问题最容易理解和编程的方案之一
• 解决方案还是分为两步：
  • 首先将合法走棋次序表示为一个图
  • 采用图搜索算法搜寻一个长度为（行×列-1）的路径，路径上包含每个顶点恰一次

构建骑士周游图

• 为了用图表示骑士周游问题，我们将棋盘上的每一格表示为一个顶点，同时将骑士的每一次合理走法表示为一条边。

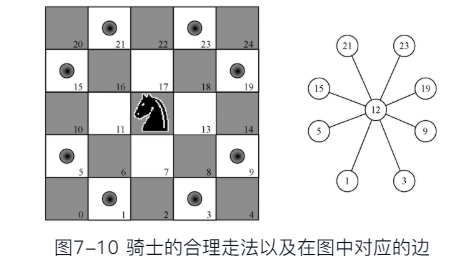
合法走棋位置函数

def genLegalMoves(x, y, bdSize):
    newMove = []
    # 马走日8个格子
    moveOffsets = [
        (-1, -2), (-1, 2), (-2, -1), (-2, 1),
        (1, -2), (1, 2), (2, -1), (2, 1)
    ]
    for i in moveOffsets:
        newX = x+i[0]
        newY = y+i[1]
        if legalCoord(newX, bdSize) and legalCoord(newY, bdSize):
            newMove.append((newX, newY))
    return newMove

# 确保不会走出棋盘
def legalCoord(x, bdSize):
    if x >= 0 and x < bdSize:
        return True
    else:
        return False

构建走棋关系图

def knightGraph(bdSize):
    ktGraph = Graph()
    for row in range(bdSize):
        for col in range(bdSize):
            nodeId = posToNodeId(row, col, bdSize)
            newPositions = genLegalMoves(row, col, bdSize)
            for e in newPositions:
                nid = posToNodeId(e[0], e[1].bdSize)
                ktGraph.addEdge(nodeId, nid)
    return ktGraph

def posToNodeId(row, col, bdSize):
    return row*bdSize+col

8×8棋盘生成的图

具有336条边， 相比起全连接的4096条边， 仅8.2%， 还是稀疏图

---

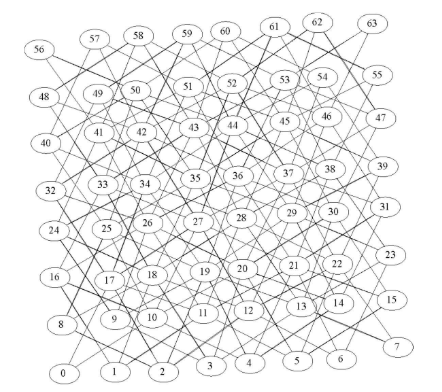
骑士周游算法实现

简介

• 用于解决骑士周游问题的图搜索算法是深度优先搜索（Depth First Search,简称DFS）
• 相比前述的广度优先搜索， 其逐层建立搜索树的特点
• 深度优先搜索是沿着树的单支尽量深入向下搜索
  
  如果到无法继续的程度还未找到问题解就回溯上一层再搜索下一支
• DFS的两个实现算法
  • 一个DFS算法用于解决骑士周游问题，其特点是每个顶点仅访问一次
  • 另一个DFS算法更为通用，允许顶点被重复访问，可作为其它图算法的基础

深度优先搜索解决骑士周游的关键思路

• 如果沿着单支深入搜索到无法继续（所有合法移动都已经被走过了）时路径长度还没有达到预定值（8×8棋盘为63）；那么就清除颜色标记，返回到上一层换一个分支继续深入搜索
• 引入一个栈来记录路径并实施返回上一层的回溯操作

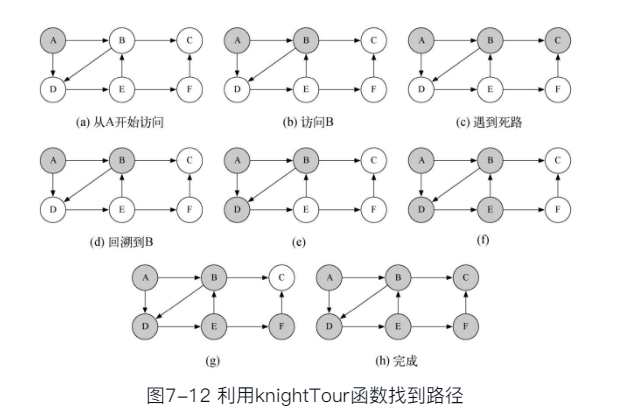
代码实现

def knightTour(n, path, u, limit):
    """
    n:层次；
    path:路径；
    u:当前顶点；
    limit:搜索总深度
    """
    u.setColor('gray')
    # 当前点加入路径
    path.append(u)
    if n < limit:
        # 对所有合法移动逐一深入
        nbrList = list(u.getConnections())
        i = 0
        done = False
        while i < len(nbrList) and not done:
            if nbrList[i].getColor() == 'white': # 选择未经过的顶点深入
                done = knightTour(n+1, path, nbrList[i], limit) # 层次+1，递归深入
            i += 1
        # 都无法完成总深度，回溯，试本层下一个顶点
        if not done:
            path.pop()
            u.setColor('white')
    else:
        done = True
    return done

---

骑士周游算法分析

• 上述算法的性能高度依赖于棋盘大小：
  • 就5×5棋盘，约1.5秒可以得到一个周游路径
  • 但8×8棋盘，则要半个小时以上才能得到一个解
• 目前实现的算法， 其复杂度为O(kn)， 其中n是棋盘格数目
  
  这是一个指数时间复杂度的算法！其搜索过程表现为一个层次为n的树

---

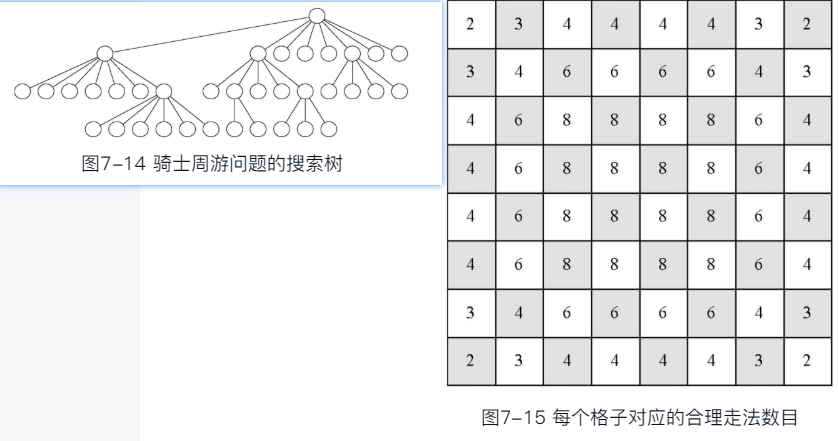
骑士周游算法改进

Warnsdorff算法

对nbrList的灵巧构造，以特定方式排列顶点访问次序可以使得8×8棋盘的周游路径搜索时间降低到秒级！

• 初始算法中nbrList， 直接以原始顺序来确定深度优先搜索的分支次序
• 新的算法， 仅修改了遍历下一格的次序
  • 将u的合法移动目标棋盘格排序为：具有最少合法移动目标的格子优先搜索

优化代码

def orderByAvail(n):
    resList = []
    for v in n.getConnections():
        if v.getColor() == 'white':
            c = 0
            for w in v.getConnections():
                if w.getColor() == 'white':
                    c += 1
            resList.append((c, v))
    resList.sort(key=lambda x: x[0])
    return [y[1] for y in resList]

启发式规则heuristic

• 采用先验的知识来改进算法性能的做法，称作为“启发式规则heuristic”
• 启发式规则经常用于人工智能领域；
• 可以有效地减小搜索范围、更快达到目标等等；
  • 如棋类程序算法，会预先存入棋谱、布阵口诀、高手习惯等“启发式规则”，能够在最短时间内从海量的棋局落子点搜索树中定位最佳落子。
    • 例如：黑白棋中的“金角银边”口诀，指导程序优先占边角位置等等

---

通用深度优先搜索

介绍

• 骑士周游问题是一种特殊的对图进行深度优先搜索

  • 其目的是建立一个没有分支的最深的深度优先树
  • 表现为一条线性的包含所有节点的退化树

• 一般的深度优先搜索目标是在图上进行尽量深的搜索， 连接尽量多的顶点， 必要时可以进行分支（创建了树）

  • 有时候深度优先搜索会创建多棵树，称为“深度优先森林”

• 深度优先搜索同样要用到顶点的“前驱”属性， 来构建树或森林

  • 另外要设置“发现时间”和“结束时间”属性

    • 前者是在第几步访问到这个顶点（设置灰色）
    • 后者是在第几步完成了此顶点探索（设置黑色）

    这两个新属性对后面的图算法很重要

• 带有DFS算法的图实现为Graph的子类

  • 顶点Vertex增加了成员Discovery及Finish
  • 图Graph增加了成员time用于记录算法执行的步骤数目

通用的深度优先搜索算法代码

• BFS采用队列存储待访问顶点
• DFS则是通过递归调用，隐式使用了栈

class DFSGraph(Graph):
    def __init__(self):
        super.__init__()
        self.time = 0

    def dfs(self):
				# 颜色初始化
        for aVertex in self: # 遍历所有顶点
            aVertex.setColor('white')
            aVertex.setPred(-1)
				# 如果还有未包括的顶点，则建森林
        for aVertex in self:
            if aVertex.getColor() == 'white':
                self.adfvisit(aVertex)

    def dfsvisit(self, startVertex):
        startVertex.setColor('gray')
				# 算法的步数
        self.time += 1
        startVertex.setDiscovery(self.time)
        for nextVertex in startVertex.getConnections():
            if nextVertex.getColor() == 'white':
                nextVertex.setPred(startVertex)
								# 深度优先递归访问
                self.dfsvisit(nextVertex)
        startVertex.setColor('black')
        self.time+1
        startVertex.setFinish(self.time)

算法分析

• DFS构建的树， 其顶点的“发现时间”和“结束时间”属性， 具有类似括号的性质
  • 即一个顶点的“发现时间”总小于所有子顶点的“发现时间”
  • 而“结束时间”则大于所有子顶点“结束时间”比子顶点更早被发现，更晚被结束探索

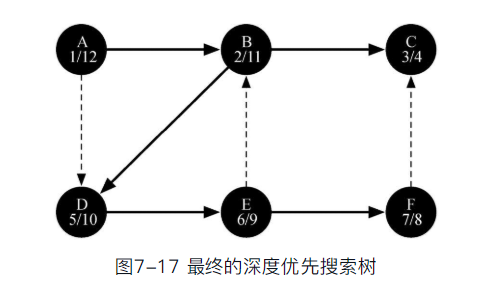
• DFS运行时间同样也包括了两方面：
  • dfs函数中有两个循环，每个都是|V|次，所以是O(|V|)
  • 而dfsvisit函数中的循环则是对当前顶点所连接的顶点进行，而且仅有在顶点为白色的情况下才进行递归调用，所以对每条边来说只会运行一步，所以是O(|E|)
  • 加起来就是和BFS一样的O(|V|+|E|)