快速傅里叶变换（FFT）随笔

终于学会了FFT，水一篇随笔记录一下

前置知识网上一大堆，这里就不多赘述了，直接切入正题

01 介绍FFT

这里仅指出FFT在竞赛中的一般应用，即优化多项式乘法

一般情况下，计算两个规模为$n$的多项式相乘的结果，复杂度为$O(n^2)$，但是神奇的FFT可以将其优化至$O(nlogn)$

FFT的过程一般为：

多项式的系数表示$\longrightarrow$多项式的点值表示$\longrightarrow$多项式的系数表示


网上对每一步的叫法都有一定出入，这里称第一步变换为快速傅里叶变换，第二步为快速傅里叶逆变换

02快速傅里叶变换

先指出，接下来的每个$n$都是$2$的整数次幂

首先我们有一个已知系数表达的$n$项的多项式

$A(x)=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}$

要确定其的点值表达$(y_0,y_1,y_2,\dots,y_{n-1})$，朴素的做法就是取$n$个不同值代进去，这么做显然是$O(n^2)$

下面介绍快速傅里叶变换的做法

首先将多项式按照奇偶分类

$A(x)=(a_0+a_2x^2+\dots+a_{n-2}x^{n-2})+(a_1x+a_3x^3+\dots+a_{n-1}x^{n-1})$

$A(x)=(a_0+a_2x^2+\dots+a_{n-2}x^{n-2})+x\cdot(a_1+a_3x^2+\dots+a_{n-1}x^{n-2})$

设

$A_1(x)=a_0+a_2x+\dots+a_{n-2}x^{\tfrac{n-2}{2}}$

$A_2(x)=a_1+a_3x+\dots+a_{n-1}x^{\tfrac{n-2}{2}}$

不难发现

$A(x)=A_1(x^2)+xA_2(x^2)$

令$k<\frac{n}{2}$

将$\omega_{n}^k$代入得

$A(\omega_{n}^k)=A_1(\omega_{n}^{2k})+\omega_{n}^{k}A_2(\omega_{n}^{2k})$

$A(\omega_{n}^k)=A_1(\omega_{\tfrac{n}{2}}^{k})+\omega_{n}^{k}A_2(\omega_{\tfrac{n}{2}}^{k})$

将$\omega_{n}^{k+\frac{n}{2}}$代入得

$A(\omega_{n}^{k}+\tfrac{n}{2})=A_1(\omega_{n}^{2k+n})+\omega_{n}^{k+\tfrac{n}{2}}A_2(\omega_{n}^{2k+n})$

$A(\omega_{n}^{k}+\tfrac{n}{2})=A_1(\omega_{n}^{2k}\cdot\omega_{n}^{n})-\omega_{n}^{k}A_2(\omega_{n}^{2k}\cdot\omega_{n}^{n})$

$A(\omega_{n}^{k}+\tfrac{n}{2})=A_1(\omega_{n}^{2k})-\omega_{n}^{k}A_2(\omega_{n}^{2k})$

$A(\omega_{n}^k)=A_1(\omega_{\tfrac{n}{2}}^{k})-\omega_{n}^{k}A_2(\omega_{\tfrac{n}{2}}^{k})$

显然的，这两个式子只有常数项不同

当$k$取遍$[0,\frac{n}{2}-1]$中所有值时$k+\dfrac{n}{2}$也取遍$[\dfrac{n}{2},n-1]$中所有值

因此，问题的规模缩小了一半，我们只需要在$[0,\dfrac{n}{2}-1]$中枚举$k$，这样就可以算出$A(\omega_{n}^i)\quad(i\in[0,n-1])$的所有值

如果我们已知$A_1(x),A_2(x)$在$\omega_{\tfrac{n}{2}}^0,\omega_{\tfrac{n}{2}}^1,\dots,\omega_{\tfrac{n}{2}}^{\tfrac{n}{2}-1}$的值，通过上面的两个式子就可以在$O(n)$的时间内求出$A(x)$

而求$A_1(x),A_2(x)$正好是求$A(x)$的子问题，并且可以递归求解

03快速傅里叶逆变换

在上面我们将一个多项式的系数表示转换成了点值表示，这里我们要研究将一个多项式的点值表示转换成系数表示

记$(a_0,a_1,\dots,a_{n-1})$是$A(x)$的系数向量，而我们已知$A(x)$的点值表达为$(A(x_0),A(x_1),\dots,A(x_{n-1}))$

设向量$(d_0,d_1,\dots,d_{n-1})$是以$(a_0,a_1,\dots,a_{n-1})$为系数向量，快速傅里叶变换求得的点值表示

构造一个多项式$F(x)=d_0+d_1x+d_2x^2+\dots+d_{n-1}x^{n-1}$

设$(c_0,c_1,\dots,c_{n-1})$是$F(x)$在$x=\omega_n^{-k}$时的点值表示，即$c_k=F(\omega_n^k)$，也就是$c_k=\sum_{i=0}^{n-1}d_i(\omega_n^{-k})^i$

我们知道$d_k=A(\omega_n^k)$，也就是$d_k=\sum_{j=0}^{n-1}a_j(\omega_n^k)^j$

联立上面两个和式得

$c_k=\sum_{i=0}^{n-1} [\sum_{j=0}^{n-1}a_j(\omega_n^i)^j] (\omega_n^{-k})^i$

$\quad \:=\sum_{i=0}^{n-1} \sum_{j=0}^{n-1}a_j(\omega_n^j)^i (\omega_n^{-k})^i$

$\quad \:=\sum_{j=0}^{n-1} a_j \sum_{i=0}^{n-1} (\omega_n^j \omega_n^{-k})^i$

$\quad \:=\sum_{j=0}^{n-1} a_j \sum_{i=0}^{n-1} (\omega_n^{j-k})^i$

我们分情况讨论后面的一个和式$\sum_{i=0}^{n-1} (\omega_n^{j-k})^i$

$j \neq\ k$

那么后面的一个和式就转换为一个等比求和

$\sum_{i=0}^{n-1} (\omega_n^{j-k})^i=\frac{\omega_n^0 [1-(\omega_n^{j-k})^n]}{1-\omega_n^{j-k}}$

$\qquad \qquad \quad \: \: \:=\frac{1-(\omega_n^{j-k})^n}{1-\omega_n^{j-k}}$

$\qquad \qquad \quad \: \: \:=\frac{1-(\omega_n^n)^{j-k}}{1-\omega_n^{j-k}}$

$\qquad \qquad \quad \: \: \:=\frac{1-1^{j-k}}{1-\omega_n^{j-k}}$

$\qquad \qquad \quad \: \: \:=\frac{0}{1-\omega_n^{j-k}}$

$\qquad \qquad \quad \: \: \:=0$

$j = k$

那么$\omega_n^{j-k} = 1$

$\sum_{i=0}^{n-1} (\omega_n^{j-k})^i = n$

由上面两种情况，我们知道当且仅当$j = k$时，整个式子才有值，其余情况都为$0$

所以有

$c_j=a_jn$

$a_j = \frac{c_j}{n}$

到这里，我们就求出了$A(x)$的系数表达

从整个分析过程看，我们是将$A(x)$的点值表示$(A(x_0),A(x_1),\dots,A(x_{n-1}))$当作一个新的多项式$F(x)$的系数表示，再对$F(x)$做快速傅里叶变换得到$(c_0,c_1,\dots,c_{n-1})$，然后再除以$n$就得到$A(x)$的系数表示了。需要指出的是，快速傅里叶变换中$x=\omega_n^k$但是在逆变换中代入的是$\omega_n^{-k}$

04实现

学会了前面的方法，具体实现就不难了

对于求$C(x)=A(x) \cdot B(x)$

将$A(x)$和$B(x)$都转化成点值表达，即$(a_0,a_1,\dots,a_{n-1})$和$(b_0,b_1,\dots,b_{n-1})$

对应相乘$(a_0b_0,a_1b_1,\dots,a_{n-1}b_{n-1})$，再将这一结果变换成$C(x)$的系数表达就完成了

贴一份C++的代码，这是洛谷上的FFT板子题P3803

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define MAXN 4000006
using namespace std;
class complex
{
public:
    complex(){}
    complex(double a,double b)
    {
        this->a=a;
        this->b=b;
    }
    double a,b;
}a[MAXN],b[MAXN];
complex operator+ (complex x,complex y)
{
    return complex(x.a+y.a,x.b+y.b);
}
complex operator- (complex x,complex y)
{
    return complex(x.a-y.a,x.b-y.b);
}
complex operator* (complex x,complex y)
{
    return complex(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a);
}
const double pi=acos(-1.0);
void FFT(int l,complex *arr,int f)
{
    if(l==1) return;
    int dl=l>>1;
    complex a1[dl],a2[dl];
    for(int i=0;i<l;i+=2)
    {
        a1[i>>1]=arr[i];
        a2[i>>1]=arr[i+1];
    }
    FFT(dl,a1,f);
    FFT(dl,a2,f);
    complex wn=complex(cos(2.0*pi/l),sin(2.0*pi/l)*f),w=complex(1.0,0.0);
    for(int i=0;i<dl;i++,w=w*wn)
    {
        arr[i]=a1[i]+w*a2[i];
        arr[i+dl]=a1[i]-w*a2[i];
    }
}
int n,m,N;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++)
        scanf("%lf",&a[i].a);
    for(int i=0;i<=m;i++)
        scanf("%lf",&b[i].a);
    N=1;
    while(N<n+m+1) N<<=1;
    FFT(N,a,1);
    FFT(N,b,1);
    for(int i=0;i<N;i++)
        a[i]=a[i]*b[i];
    FFT(N,a,-1);
    for(int i=0;i<n+m+1;i++)
        printf("%d ",(int)(a[i].a/N+0.5));
    puts("");
    return 0;
}

闲着没事干，再贴一份Python的

import numpy as np

pi = np.arccos(-1.0)

def read():
    def get_numbers():
        try:
            read.s = input().split()
            read.s_len = len(read.s)
            if read.s_len == 0:
                get_numbers()
            read.cnt = 0
            return 1
        except:
            return 0

    if not hasattr(read, 'cnt'):
        if not get_numbers():
            return 0
    if read.cnt == read.s_len:
        if not get_numbers():
            return 0
    read.cnt += 1
    return eval(read.s[read.cnt - 1])

n = int(read())
m = int(read())

class Complex:
    # 复数类

    def __init__(self, a=0.0, b=0.0):
        self.a = a
        self.b = b

    def __add__(self, other):
        return Complex(self.a + other.a, self.b + other.b)

    def __sub__(self, other):
        return Complex(self.a - other.a, self.b - other.b)

    def __mul__(self, other):
        return Complex(self.a * other.a - self.b * other.b, self.a * other.b + self.b * other.a)

def fft(num, f, args):
    if num == 1:
        return
    div_num = num >> 1
    a1 = []
    a2 = []
    for i in range(0, num, 2):
        a1.append(args[i])
        a2.append(args[i + 1])
    fft(div_num, f, a1)
    fft(div_num, f, a2)
    wn = Complex(np.cos(2.0 * pi / num), np.sin(2.0 * pi / num) * f)
    w = Complex(1.0, 0.0)

    for i in range(0, div_num):
        args[i] = a1[i] + w * a2[i]
        args[i + div_num] = a1[i] - w * a2[i]
        w = w * wn

aa = []
bb = []
for j in range(0, n + 1):
    aa.append(Complex(float(read()), 0.0))
for j in range(0, m + 1):
    bb.append(Complex(float(read()), 0.0))

nn = 1
while nn < n + m + 1:
    nn <<= 1

for j in range(n + 1, nn):
    aa.append(Complex(0.0, 0.0))
for j in range(m + 1, nn):
    bb.append(Complex(0.0, 0.0))

fft(nn, 1, aa)
fft(nn, 1, bb)

for j in range(0, nn):
    aa[j] = aa[j] * bb[j]
fft(nn, -1, aa)

for j in range(0, n + m + 1):
    print(int(aa[j].a / nn + 0.5), end=' ')

无奈Python实在是太慢了……

05结语

总算是学会了快速傅里叶变换，某种程度上说是弥补了过去的某些遗憾吧。

这里贴一张大佬的图，解释了FFT的思路

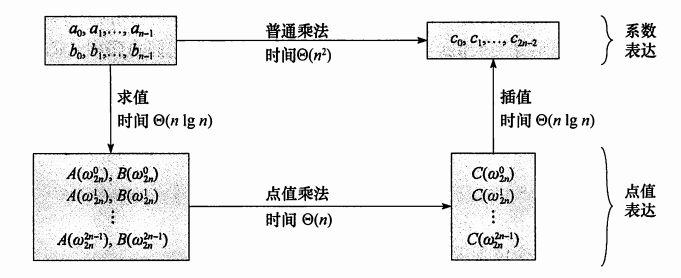
这里也推荐一下大佬的博客，以供参考

快速傅里叶变换(FFT)详解 - 自为风月马前卒 - 博客园 (cnblogs.com)

一小时学会快速傅里叶变换（Fast Fourier Transform） - 知乎 (zhihu.com)