洛谷 P7156 - [USACO20DEC] Cowmistry P（分类讨论+trie 树上 dp）

题面传送门

题意：

给出集合 \(S=[l_1,r_1]\cup[l_2,r_2]\cup[l_3,r_3]\cup\dots\cup[l_n,r_n]\) 和整数 \(k\)，求有多少个三元组 \((a,b,c)\) 满足：

• \(a,b,c\in S\)，\(a<b<c\)
• \(a,b,c\) 两两异或得到的值均 \(\leq k\)

答案对 \(10^9+7\) 取模。

\(1\leq n\leq 2\times 10^4\)，\(0\leq l_1\leq r_1\lt l_2\leq r_2\lt\dots\lt l_n\leq r_n\leq 10^9\)

Yet another 1e9+7

Yet another 计数 dp

Yet another 我做不出来的题

阿巴细节题。

首先考虑优雅的暴力，也就是 \(\max(k,r_n)\leq 10^6\) 那一档部分分。

建一棵包含 \(S\) 所有元素的 trie 树。

设 \(dp1_i\) 表示选择的三个数均在 \(i\) 的子树中的方案数。假设我们当前考虑到从高到低的第 \(x\) 位。

可以分为四种情况转移：

1. 选择的三个数均在 \(i\) 的左子树内。这种情况又可分为两种情况：如果 \(k\) 的从高到低的第 \(x\) 位为 \(1\)，那么不论选哪三个点，它们两两异或起来从高到低第 \(x\) 位都为 \(0\)。故不论选哪三个点都满足条件，贡献为 \(\dbinom{siz_{ch_{i,0}}}{3}\) ；如果 \(k\) 从高到低的第 \(x\) 位为 \(0\)，那么贡献就是 \(dp1_{ch_{i,0}}\)。
2. 选择的三个数均在 \(i\) 的右子树内，与第一种情况几乎一样。
3. 选择的三个数中，其中两个数 \(a,b\) 在 \(i\) 的左子树内，一个数 \(c\) 在 \(i\) 的右子树内。由于 \(b\oplus c\) 从高到低的第 \(x\) 位为 \(1\)，故这种情况只有当 \(k\) 的从高到低的第 \(x\) 位为 \(1\) 的情况下才能发生。
4. 选择的三个数中，其中一个数 \(a\) 在 \(i\) 的左子树内，一个数 \(b,c\) 在 \(i\) 的右子树内，与第三种情况几乎一样。

不难发现，在这四种情况中前两种情况都是可以直接转移的，而后两种无法直接表示出来，需要引入另一个状态。

再设 \(dp2_{i,j}\) 表示选择的三个数中两个数在 \(i\) 的子树中，一个在 \(j\) 的子树中的方案数。

继续分情况讨论，可以分为六种情况：

1. 在 \(i\) 子树中的两个数都在 \(i\) 的左子树中，在 \(j\) 子树中的数在 \(j\) 的左子树中。这种情况又可分为两种情况：如果 \(k\) 的从高到低的第 \(x\) 位为 \(1\)，那么不论选哪三个点，它们两两异或起来从高到低第 \(x\) 位都为 \(0\)。故不论选哪三个点都满足条件，贡献为 \(\dbinom{siz_{ch_{i,0}}}{2}\times siz_{ch_{j,0}}\)。 如果 \(k\) 从高到低的第 \(x\) 位为 \(0\)，那么贡献就是 \(dp2_{ch_{i,0},ch_{j,0}}\)。
2. 在 \(i\) 子树中的两个数 \(a,b\) 都在 \(i\) 的左子树中，在 \(j\) 子树中的数 \(c\) 在 \(j\) 的右子树中。由于 \(a\oplus c\) 从高到低的第 \(x\) 位为 \(1\)，所以这种情况只有在当 \(k\) 的从高到低的第 \(x\) 位为 \(1\) 的情况下才能发生。这种情况产生的贡献为 \(dp2_{ch_{i,0},ch_{j,1}}\)
3. 在 \(i\) 子树中的两个数 \(a,b\) 中 \(a\) 在 \(i\) 的左子树中，\(b\) 在 \(i\) 的右子树中，在 \(j\) 子树中的数 \(c\) 在 \(j\) 的左子树中。由于 \(b\oplus c\) 从高到低的第 \(x\) 位为 \(1\)，所以这种情况只有在当 \(k\) 的从高到低的第 \(x\) 位为 \(1\) 的情况下才能发生。我们还注意到，不论 \(a\) 为何值都有 \(a\oplus b<a\oplus c<b\oplus c\)， 也就是说，不论 \(a\) 取何值，只要 \(b,c\) 满足条件，\(a\) 一定满足条件。求出满足条件的 \(b,c\) 个数后乘一个 \(siz_{ch_{i,0}}\) 就行了。
4. 在 \(i\) 子树中的两个数 \(a,b\) 中 \(a\) 在 \(i\) 的左子树中，\(b\) 在 \(i\) 的右子树中，在 \(j\) 子树中的数 \(c\) 在 \(j\) 的右子树中，与第三种情况几乎一样，只不过变成了求出满足条件的 \(a,c\) 的个数 。
5. 在 \(i\) 子树中的两个数 \(a,b\) 都在 \(i\) 的右子树中，在 \(j\) 子树中的数 \(c\) 在 \(j\) 的左子树中，与第二种情况几乎一样。
6. 在 \(i\) 子树中的两个数都在 \(i\) 的右子树中，在 \(j\) 子树中的数在 \(j\) 的右子树中，与第一种情况几乎一样。

但是碰到这里我们又犯难了，情况 1,2,5,6 可以直接转移，但是情况 3,4 无法通过已有状态求出满足条件的 \(b,c\) 的个数，这是我们又需要引入一个新状态。

再设 \(dp3_{i,j}\) 表示两个数 \(a,b\) 中一个数在 \(i\) 的子树中，一个在 \(j\) 的子树中的方案数。

又可以分四种情况：

1. \(a\) 在 \(i\) 的左子树中，\(b\) 在 \(j\) 的左子树中，这种情况又可分为两种情况：如果 \(k\) 的从高到低的第 \(x\) 位为 \(1\)，那么不论选哪两个点，它们两两异或起来从高到低第 \(x\) 位都为 \(0\)。故不论选哪三个点都满足条件，贡献为 \(siz_{ch_{i,0}}\times siz_{ch_{j,0}}\)。 如果 \(k\) 从高到低的第 \(x\) 位为 \(0\)，那么贡献就是 \(dp3_{ch_{i,0},ch_{j,0}}\)。

2. \(a\) 在 \(i\) 的左子树中，\(b\) 在 \(j\) 的右子树中。由于 \(a\oplus b\) 从高到低的第 \(x\) 位为 \(1\)，所以这种情况只有在当 \(k\) 的从高到低的第 \(x\) 位为 \(1\) 的情况下才能发生。

3. \(a\) 在 \(i\) 的右子树中，\(b\) 在 \(j\) 的左子树中，与第二种情况几乎一样。

4. \(a\) 在 \(i\) 的右子树中，\(b\) 在 \(j\) 的右子树中，与第一种情况几乎一样。

算下时间复杂度：\(dp1\) 的时间复杂度肯定是没问题的，加个记忆化每个 \(dp1_i\) 最多被计算一次。关键是 \(dp2\) 和 \(dp3\)，\(dp2\) 和 \(dp3\) 状态是二维的。可合法的状态数真的是 \(n^2\) 吗？非也。拿 \(dp2\) 举例，只有当 \(k\) 的第 \(x\) 位为 \(0\) 的时候才会调用 \(dp2_{ch_{i,0},ch_{j,0}}\) 和 \(dp2_{ch_{i,1},ch_{j,1}}\)，当 \(k\) 的第 \(x\) 位为 \(1\) 的时候才会调用 \(dp2_{ch_{i,0},ch_{j,1}}\) 和 \(dp2_{ch_{i,1},ch_{j,0}}\)。稍微观察下即可发现，\(i\) 与 \(j\) 表示的数异或起来肯定是 \(k\) 的一个前缀。这意味着对于每个 \(i\) 有唯一的 \(j\) 与之对应，故合法状态数只有 \(\mathcal O(m)\)，其中 \(m\) 为 trie 数上的点数。故这个“优雅的暴力”是没问题的（真 nm 优雅）。

最后考虑 \(k,r_n\leq 10^9\) 的情况。其实想到这一步本题就已经做完了 \(80\%\) 了，虽然到这一步只包含了本题 \(40\%\) 的部分分。

我们发现待插入的数很多，高达 \(10^9\)，但是这些数都是一段一段区间，区间个数只有 \(2\times 10^4\)。于是我们可以想到一个东西叫做线段树，可以通过线段树的思想将每个区间拆分成 \(\log 10^9\) 个长度为 \(2\) 的整数次幂的区间插入 trie 树。这样一来我们可以得到这样的 trie 树：trie 树上每个叶子节点代表一个大小为 \(2^m\) 的满二叉树。

这样说有些抽象，举个例子，譬如我们要插入区间 \([0,6]\)，如果按照之前的暴力我们会这样插：

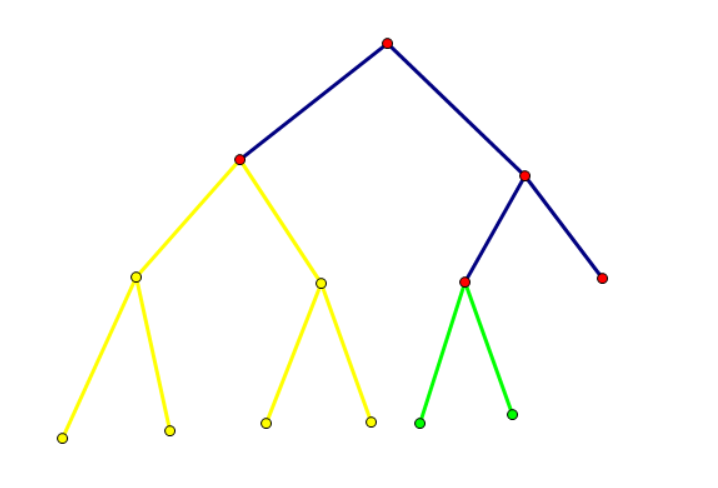
但我们发现，黄色部分和绿色部分都是满二叉树，根本不用把它们建出来，所以我们索性把它们缩成一个“大点”：

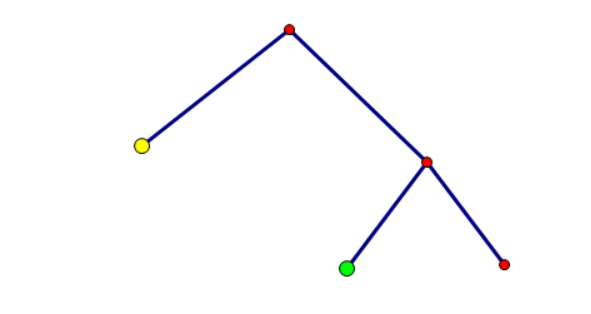
但是这样还是不太行啊？如果你 \(dfs\) 到一个“大点”，对应到 \(dp\) 值怎么计算呢？

可以考虑额外建 \(31\) 个节点，编号为 \(0,1,2,\dots,30\)，节点 \(i\) 的左右儿子都是节点 \(i-1\)，这样大小为 \(2^m\) 的子树就等价于节点 \(m\)，\(dfs\) 的时候直接在这 \(31\) 个节点上记录 \(dp\) 值就可以了。

代码不长，也就 100 行而已，不过细节实在是太太太太太太多了，这篇题解也写了整整 1 个小时。。。

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
   x=0;char c=getchar();T neg=1;
   while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
   while(isdigit(c)) x=x*10+c-'0',c=getchar();
   x*=neg;
}
const int MAXN=2e4;
const int LOG_N=30;
const int MAXT=1e6;
const int MAX=(1<<LOG_N)-1;
const int MOD=1e9+7;
const int TWO=5e8+4;
const int SIX=166666668;
int n,k,siz[MAXT+5],ch[MAXT+5][2],ncnt=LOG_N+1,rt=LOG_N+1,dep[MAXT+5];
bool isend[MAXT+5];
void update(int &k,int l,int r,int nl,int nr,int d){
   if(l==nl&&nr==r){k=LOG_N-d;return;}
   if(!~k) k=++ncnt,dep[k]=d;int mid=(l+r)>>1;
//	printf("%d %d %d %d %d %d\n",k,l,r,nl,nr,d);
   if(nr<=mid) update(ch[k][0],l,mid,nl,nr,d+1);
   else if(nl>mid) update(ch[k][1],mid+1,r,nl,nr,d+1);
   else update(ch[k][0],l,mid,nl,mid,d+1),update(ch[k][1],mid+1,r,mid+1,nr,d+1);
   siz[k]=siz[ch[k][0]]+siz[ch[k][1]];
}
int dp1[MAXT+5];
map<int,int> dp2[MAXT+5],dp3[MAXT+5];
int calc1(int x);
int calc2(int x,int y);
int calc3(int x,int y);
//calc1: 3 nodes in subtree of x
//calc2: 2 nodes in subtree of x and 1 node in subtree of y
//calc3: 1 nodes in subtree of x and 1 node in subtree of y
int calc1(int x){
//	if(x==0||x==1) return 0;
   if(~dp1[x]) return dp1[x];
   dp1[x]=0;
   if(~ch[x][0]){
   	if(k>>(LOG_N-dep[x]-1)&1) dp1[x]=(dp1[x]+1ll*siz[ch[x][0]]*(siz[ch[x][0]]-1)%MOD*(siz[ch[x][0]]-2)%MOD*SIX%MOD)%MOD;
   	else dp1[x]=(dp1[x]+calc1(ch[x][0]))%MOD;
   }
   if(~ch[x][1]){
   	if(k>>(LOG_N-dep[x]-1)&1) dp1[x]=(dp1[x]+1ll*siz[ch[x][1]]*(siz[ch[x][1]]-1)%MOD*(siz[ch[x][1]]-2)%MOD*SIX%MOD)%MOD;
   	else dp1[x]=(dp1[x]+calc1(ch[x][1]))%MOD;
   }
   if(~ch[x][0]&&~ch[x][1]) if(k>>(LOG_N-dep[x]-1)&1){
   	dp1[x]=(dp1[x]+calc2(ch[x][0],ch[x][1]))%MOD;
   	dp1[x]=(dp1[x]+calc2(ch[x][1],ch[x][0]))%MOD;
   }
//	printf("%d %d\n",x,dp1[x]);
   return dp1[x];
}
int calc2(int x,int y){
//	if(!x) return 0;
   if(dp2[x].find(y)!=dp2[x].end()) return dp2[x][y];
   dp2[x][y]=0;
   if(~ch[x][0]&&~ch[y][0]){
   	if(k>>(LOG_N-dep[x]-1)&1)
   		dp2[x][y]=(dp2[x][y]+1ll*siz[ch[x][0]]*(siz[ch[x][0]]-1)%MOD*TWO%MOD*siz[ch[y][0]]%MOD)%MOD;
   	else dp2[x][y]=(dp2[x][y]+calc2(ch[x][0],ch[y][0]))%MOD;
   }
   if(~ch[x][0]&&~ch[y][1]) if(k>>(LOG_N-dep[x]-1)&1) dp2[x][y]=(dp2[x][y]+calc2(ch[x][0],ch[y][1]))%MOD;
   if(~ch[x][0]&&~ch[x][1]&&~ch[y][0]) if(k>>(LOG_N-dep[x]-1)&1) dp2[x][y]=(dp2[x][y]+1ll*calc3(ch[x][1],ch[y][0])*siz[ch[x][0]]%MOD)%MOD;
   if(~ch[x][0]&&~ch[x][1]&&~ch[y][1]) if(k>>(LOG_N-dep[x]-1)&1) dp2[x][y]=(dp2[x][y]+1ll*calc3(ch[x][0],ch[y][1])*siz[ch[x][1]]%MOD)%MOD;
   if(~ch[x][1]&&~ch[y][0]) if(k>>(LOG_N-dep[x]-1)&1) dp2[x][y]=(dp2[x][y]+calc2(ch[x][1],ch[y][0]))%MOD;
   if(~ch[x][1]&&~ch[y][1]){
   	if(k>>(LOG_N-dep[x]-1)&1)
   		dp2[x][y]=(dp2[x][y]+1ll*siz[ch[x][1]]*(siz[ch[x][1]]-1)%MOD*TWO%MOD*siz[ch[y][1]]%MOD)%MOD;
   	else dp2[x][y]=(dp2[x][y]+calc2(ch[x][1],ch[y][1]))%MOD;
   }
//	printf("c2 %d %d %d\n",x,y,dp2[x][y]);
   return dp2[x][y];
}
int calc3(int x,int y){
   if(!x) return 1;
   if(dp3[x].find(y)!=dp3[x].end()) return dp3[x][y];
   dp3[x][y]=0;
   if(~ch[x][0]&&~ch[y][0]){
   	if(k>>(LOG_N-dep[x]-1)&1) dp3[x][y]=(dp3[x][y]+1ll*siz[ch[x][0]]*siz[ch[y][0]]%MOD)%MOD;
   	else dp3[x][y]=(dp3[x][y]+calc3(ch[x][0],ch[y][0]))%MOD;
   }
   if(~ch[x][0]&&~ch[y][1]) if(k>>(LOG_N-dep[x]-1)&1) dp3[x][y]=(dp3[x][y]+calc3(ch[x][0],ch[y][1]))%MOD;
   if(~ch[x][1]&&~ch[y][0]) if(k>>(LOG_N-dep[x]-1)&1) dp3[x][y]=(dp3[x][y]+calc3(ch[x][1],ch[y][0]))%MOD;
   if(~ch[x][1]&&~ch[y][1]){
   	if(k>>(LOG_N-dep[x]-1)&1) dp3[x][y]=(dp3[x][y]+1ll*siz[ch[x][1]]*siz[ch[y][1]]%MOD)%MOD;
   	else dp3[x][y]=(dp3[x][y]+calc3(ch[x][1],ch[y][1]))%MOD;
   }
//	printf("c3 %d %d %d\n",x,y,dp3[x][y]);
   return dp3[x][y];
}
int main(){
   fill1(ch);
   siz[0]=1;for(int i=1;i<=LOG_N;i++) ch[i][0]=ch[i][1]=i-1,siz[i]=(1<<i),dep[i]=LOG_N-i;
   memset(dp1,-1,sizeof(dp1));scanf("%d%d",&n,&k);
   for(int i=1;i<=n;i++){int l,r;scanf("%d%d",&l,&r);update(rt,0,MAX,l,r,0);}
//	for(int i=0;i<=ncnt;i++) printf("%d %d %d %d\n",ch[i][0],ch[i][1],dep[i],siz[i]);
   printf("%d\n",calc1(rt));
   return 0;
}
/*
1 3
0 3

1 6
0 5

1 15
0 10
*/