【bzoj1150】[CTSC2007]数据备份Backup 模拟费用流+链表+堆

题目描述

你在一家 IT 公司为大型写字楼或办公楼（offices）的计算机数据做备份。然而数据备份的工作是枯燥乏味的，因此你想设计一个系统让不同的办公楼彼此之间互相备份，而你则坐在家中尽享计算机游戏的乐趣。已知办公楼都位于同一条街上。你决定给这些办公楼配对（两个一组）。每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。然而，网络电缆的费用很高。当地电信公司仅能为你提供 K 条网络电缆，这意味着你仅能为 K 对办公楼（或总计2K个办公楼）安排备份。任一个办公楼都属于唯一的配对组（换句话说，这 2K 个办公楼一定是相异的）。此外，电信公司需按网络电缆的长度（公里数）收费。因而，你需要选择这 K 对办公楼使得电缆的总长度尽可能短。换句话说，你需要选择这 K 对办公楼，使得每一对办公楼之间的距离之和（总距离）尽可能小。下面给出一个示例，假定你有 5 个客户，其办公楼都在一条街上，如下图所示。这 5 个办公楼分别位于距离大街起点 1km, 3km, 4km, 6km 和 12km 处。电信公司仅为你提供 K=2 条电缆。

上例中最好的配对方案是将第 1 个和第 2 个办公楼相连，第 3 个和第 4 个办公楼相连。这样可按要求使用 K=2 条电缆。第 1 条电缆的长度是 3km-1km=2km ，第 2 条电缆的长度是 6km-4km=2km。这种配对方案需要总长 4km 的网络电缆，满足距离之和最小的要求。

输入

输入的第一行包含整数n和k，其中n（2 ≤ n ≤100 000）表示办公楼的数目，k（1≤ k≤ n/2）表示可利用的网络电缆的数目。接下来的n行每行仅包含一个整数（0≤ s ≤1000 000 000）, 表示每个办公楼到大街起点处的距离。这些整数将按照从小到大的顺序依次出现。

输出

输出应由一个正整数组成，给出将2K个相异的办公楼连成k对所需的网络电缆的最小总长度。

样例输入

5 2
1
3
4
6
12

样例输出

4

---

题解

模拟费用流+链表+堆

本题正常题解应该是“贪心+堆”，但自从某次集训get到了模拟费用流的思想后，用在这道题里是再恰当不过了。

先前缀相减得到相邻两建筑物之间的距离，然后想到dp，但是MLE+TLE；考虑如果是费用流的话，该怎样建图？

（边权中第一个为容量，第二个为费用）

那么考虑EK费用流的过程：先选择一条最短路，加入到答案，然后将路径上的边容量-1，反向边容量+1。

那么我们模拟这个过程：

首先找到SS->S->3->2->T这条最短路，然后把它路径上的边容量-1，反向边容量+1，得到下图：

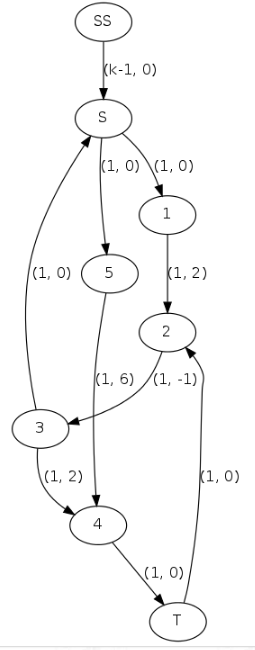
（受到画图软件的限制，只能画成这个样子，如果在草纸上推的话直接将原来的正向边反过来就行）

这个时候我们会发现3->S、T->2这两条反向边是没有用处的，所以直接删掉就好。

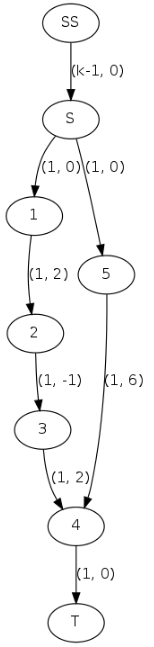
（再次尴尬）

这回我们发现，1->2、反向边2->3、3->4可以合并成一条新的边1->4，费用为2-1+2。

那么就可以在原图中把1->2、3->2、3->4的边都删了，再加上1->4的边。

使用链表实现这个过程，并用堆维护最小费用。删除什么的，对边打个标记就好了。

最后不断选出边加到答案中，最后得到的就是最小费用了。

时间复杂度$O(n\log n)$。

注意：如果选出的边是边界上的边（如1->2），那么不能进行加边操作，但是必须进行删边操作（和2相连的不能再选）

代码细节挺多

#include <cstdio>
#include <cstring>
#include <queue>
#include <utility>
#define N 100010
using namespace std;
priority_queue<pair<int , int> > q;
int tot , d[N] , last[N << 1] , next[N << 1] , val[N << 1];
bool del[N << 1];
int main()
{
	int n , k , i , u , ans = 0;
	scanf("%d%d" , &n , &k);
	for(i = 1 ; i <= n ; i ++ ) scanf("%d" , &d[i]);
	for(i = 2 ; i < n ; i ++ ) last[i] = i - 1;
	for(i = 1 ; i < n - 1 ; i ++ ) next[i] = i + 1;
	for(i = 1 ; i < n ; i ++ ) val[i] = d[i + 1] - d[i] , q.push(make_pair(-val[i] , i));
	tot = n - 1;
	while(k -- )
	{
		while(del[q.top().second]) q.pop();
		u = q.top().second , q.pop() , ans += val[u] , del[u] = del[last[u]] = del[next[u]] = 1 , next[last[u]] = last[next[u]] = 0;
		if(!last[u]) last[next[next[u]]] = 0;
		else if(!next[u]) next[last[last[u]]] = 0;
		else
		{
			val[++tot] = val[last[u]] + val[next[u]] - val[u] , last[tot] = last[last[u]] , next[tot] = next[next[u]];
			if(last[tot]) next[last[tot]] = tot;
			if(next[tot]) last[next[tot]] = tot;
			q.push(make_pair(-val[tot] , tot));
		}
	}
	printf("%d\n" , ans);
	return 0;
}