题解-POI2009 WSP-Island

Problem

bzoj1137

题意概要：给定一个凸多边形坐标。点按顺时针编号 \(1\) 到 \(n\)。任意两点之间都有一条长度为欧氏距离的边相连。边相交处可以自由穿行。有 \(m\) 条边不能走，但是可以经过这条边与其他边的交点。问从点 \(1\) 到 \(n\) 的最短路（即给定完全图，删去\(m\)边，求最短路）

\(n\leq 10^5,m\leq 10^6\)

Solution

这个题还是挺巧妙的，只是画过图后就不难了

画两张图吧，就会发现只要贪心地往\(n\)号点走即可

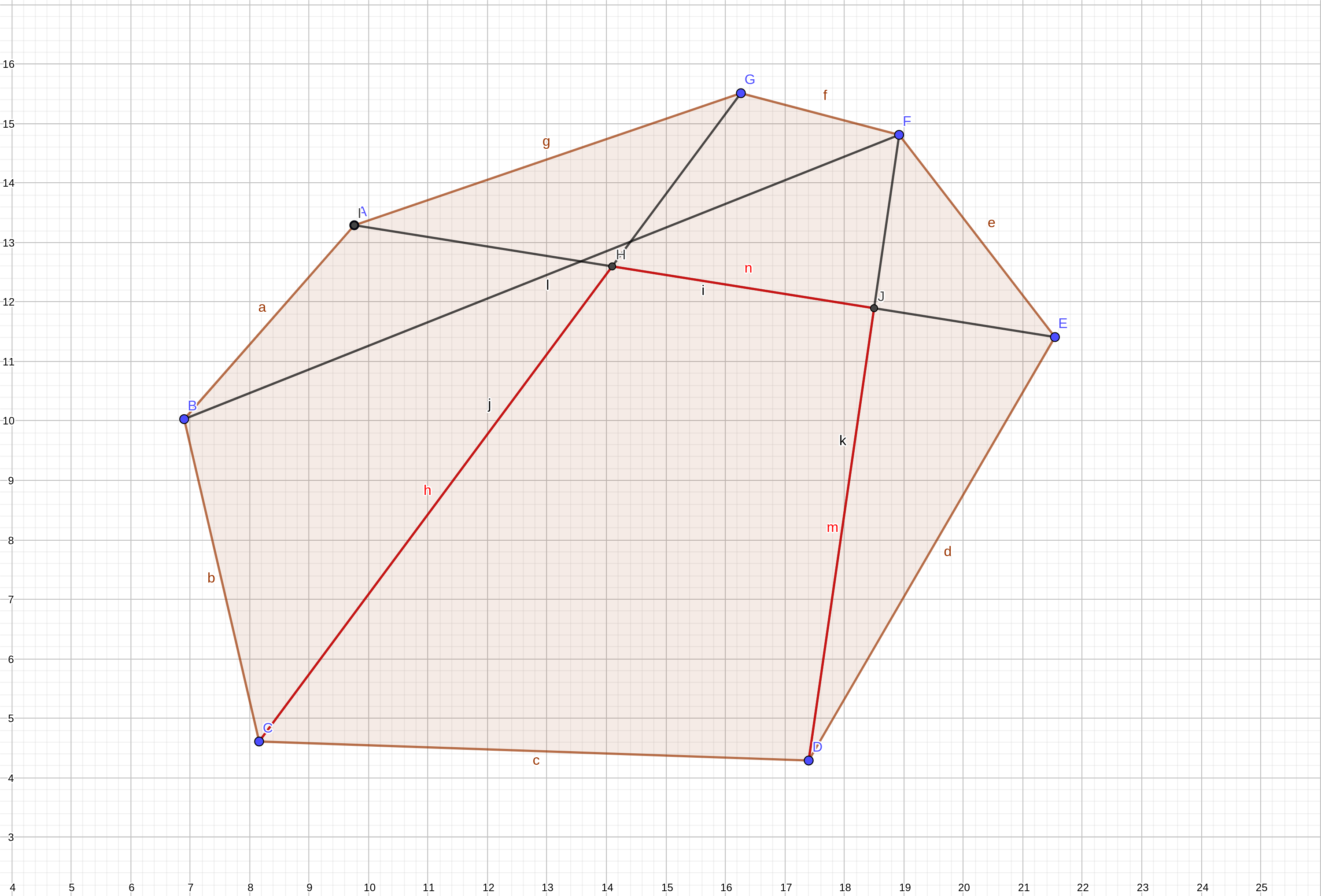
发现只要贴着里面走就行（走红色路线），进一步发现每个点连出去的的几条线只有最靠内的线有用

所以当前边数可以减少到\(n\)条，然后就……做半平面交（\(\leftarrow\)本题最巧妙的一点）

Code

#include <bits/stdc++.h>
using namespace std;

inline void read(int&x){
	char c11=getchar(),ob=0;x=0;
	while(c11^'-'&&!isdigit(c11))c11=getchar();if(c11=='-')ob=1,c11=getchar();
	while(isdigit(c11))x=x*10+c11-'0',c11=getchar();if(ob)x=-x;
}

const int N=201009,M=2001003;
const double eps=1e-8;
int n,m;bool pass=false;
struct Paris{
	int x,y;
	friend inline bool operator < (const Paris&A,const Paris&B)
		{return A.x!=B.x?A.x<B.x:A.y>B.y;}
}pr[M];

struct pnt{
	double x,y;
	inline pnt(){}
	inline pnt(const double&X,const double&Y):x(X),y(Y){}
	inline void in(){scanf("%lf%lf",&x,&y);}
	friend inline pnt operator + (const pnt&A,const pnt&B) {return pnt(A.x+B.x,A.y+B.y);}
	friend inline pnt operator - (const pnt&A,const pnt&B) {return pnt(A.x-B.x,A.y-B.y);}
	friend inline double operator * (const pnt&A,const pnt&B) {return A.x*B.y-A.y*B.x;}
	inline pnt operator * (const double&B) const {return pnt(x*B,y*B);}
}p[N],dot[N];

inline double dis(pnt A,pnt B){return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));}

struct line{
	pnt a,b;double slp;
	inline void get_slp(){slp=atan2(b.y-a.y,b.x-a.x);}
	friend inline bool operator < (const line&A,const line&B) {
		if(fabs(A.slp-B.slp)>eps)
			return A.slp<B.slp;
		return (A.b-A.a)*(B.b-A.a)<0;
	}
}l[N],q[N];

inline pnt crs(line A,line B){
	double k1=(B.b-A.a)*(A.b-A.a);
	double k2=(A.b-A.a)*(B.a-A.a);
	return B.a+(B.b-B.a)*(k2/(k1+k2));
}

inline bool chk(line A,line B,line t){pnt p=crs(A,B);return (t.b-t.a)*(p-t.a)<0;}

void work(){
	if(pass)return ;
	for(int i=1;i<=n;++i)l[i].get_slp();
	sort(l+1,l+n+1);
	int tt=0;
	for(int i=1;i<=n;++i)
		if(fabs(l[i].slp-l[i-1].slp)>eps)
			l[++tt]=l[i];
	n=tt,tt=0;int L=1,R=0;
	q[++R]=l[1],q[++R]=l[2];
	for(int i=3;i<=n;++i){
		while(L<R&&chk(q[R-1],q[R],l[i]))--R;
		while(L<R&&chk(q[L],q[L+1],l[i]))++L;
		q[++R]=l[i];
	}
	while(L<R&&chk(q[R-1],q[R],q[L]))--R;
	while(L<R&&chk(q[L],q[L+1],q[R]))++L;
	q[R+1]=q[L];
	for(int i=L;i<=R;++i)
		p[++tt]=crs(q[i],q[i+1]);
	n=tt;
}

void input(){
	read(n),read(m);
	for(int i=1;i<=n;++i)dot[i].in();
	for(int i=1;i<=m;++i)read(pr[i].x),read(pr[i].y);
	for(int i=1;i<=n;++i)pr[++m].x=i,pr[m].y=i;
	sort(pr+1,pr+m+1);
	int tt;l[tt=1].a=dot[1],l[1].b=dot[n];
	p[N-2].x=dot[1].x,p[N-2].y=dot[1].y;
	p[N-1].x=dot[n].x,p[N-1].y=dot[n].y;
	if(pr[1].x==1&&pr[1].y!=n){
		printf("%.8lf\n",dis(p[N-1],p[N-2]));
		pass=true;return ;
	}
	for(int id=1,i=1,j;id<=n;++id){
		while(i<=m&&pr[i].x<id)++i;j=n;
		while(pr[i].x==id&&pr[i].y==j)++i,--j;
		if(j>id)l[++tt].a=dot[j],l[tt].b=dot[id];
	}n=tt;
}

void print(){
	if(pass)return ;
	p[n+1]=p[1];
	double res=0.0;
	for(int i=1;i<=n;++i)
		res+=dis(p[i],p[i+1]);
	res-=dis(p[N-1],p[N-2]);
	printf("%.8lf\n",res);
}

int main(){
	input();
	work();
	print();
	return 0;
}