【机器学习】K均值算法（II）

k聚类算法中如何选择初始化聚类中心所在的位置。

在选择聚类中心时候，如果选择初始化位置不合适，可能不能得出我们想要的局部最优解。

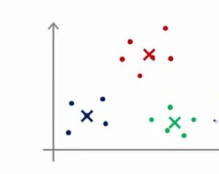
而是会出现一下情况：

为了解决这个问题，我们通常的做法是：

我们选取K<m个聚类中心。

然后随机选择K个训练样本的实例，之后令k个聚类中心分别与k个训练实例相等。

之后我们通常需要多次运行均值算法。每一次都重新初始化，然后在比较多次运行的k均值的结果，选择代价函数较小的结果。这种方法在k较小的时候可能会有效果，但是在K数量较多的时候不会有明显改善。

如何选取聚类数量

当我们研究聚类数量与畸变函数J的关系时候，发现“肘部法则”，也就是当k的数量逐渐增加时候，存在某一点成为J函数下降过程呢中的拐点。

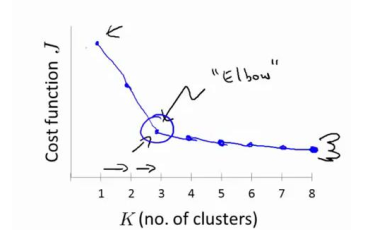
这个点之前，他的畸变的值迅速下降，在这个点之后，它的畸变值下变慢，那么看起来这个拐点通常会成为最合适的值。不过在实际情况中，我们会选择K值的数量取决于用聚类算法所需要解决的实际问题的目的出发。根据实际情况的需要选择K值的数量。