ID3算法下的决策树
网上的内容感觉又多又乱，自己写一篇决策树算法。希望对别人有所启发，对自己也是一种进步。
决策树 须知概念
信息熵 & 信息增益
熵： 熵（entropy）指的是体系的混乱的程度，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量。
信息熵（香农熵）： 是一种信息的度量方式，表示信息的混乱程度，也就是说：信息越有序，信息熵越低。例如：火柴有序放在火柴盒里，熵值很低，相反，熵值很高。
信息增益： 在划分数据集前后信息发生的变化称为信息增益。
决策树 开发流程
- 收集数据：可以使用任何方法。
- 准备数据：树构造算法只适用于标称型数据，因此数值型数据必须离散化。
- 分析数据：可以使用任何方法，构造树完成之后，我们应该检查图形是否符合预期。
- 训练算法：构造树的数据结构。
- 测试算法：使用经验树计算错误率。（经验树没有搜索到较好的资料，有兴趣的同学可以来补充）
- 使用算法：此步骤可以适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义
决策树 算法特点
- 优点：计算复杂不高。输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据
- 缺点：可能会产生过度匹配问题。（就是我们所说的过拟合，通过裁剪决策树，合并相邻的无法产生大量信息增益的叶节点，消除过度匹配）
- 适用数据类型，数值型（连续）和标称型（离散）。。。。一般用作标称
还有其他的决策树算法。最流行的是C4.5和CART。那为什么要学ID3呢？因为它简单呀。。。（简单的都折腾了半天。。。）
项目案例1: 判定鱼类和非鱼类
根据以下两个特征，将动物分成鱼类和非鱼类
整个代码的模块化：
1.输入数据
def createDataSet():
"""
Desc:
创建数据集
Args:
无需传入参数
Returns:
返回数据集和对应的label标签
"""
# dataSet 前两列是特征，最后一列对应的是每条数据对应的分类标签
dataSet = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels
2.计算香农熵
def calcShannonEnt(dataSet):
"""
Desc：
calculate Shannon entropy -- 计算给定数据集的香农熵
Args:
dataSet -- 数据集
Returns:
shannonEnt -- 返回 每一组 feature 下的某个分类下，香农熵的信息期望
"""
# -----------计算香农熵的第一种实现方式start----------------------------------------------
# 求list的长度，表示计算参与训练的数据量
numEntries = len(dataSet)
# 下面输出我们测试的数据集的一些信息
# 例如：<type 'list'> numEntries: 5 是下面的代码的输出
# print(type(dataSet), 'numEntries: ', numEntries) # 计算分类标签label出现的次数
labelCounts = {}
# the the number of unique elements and their occurance
for featVec in dataSet:
# 将当前实例的标签存储，即每一行数据的最后一个数据代表的是标签
currentLabel = featVec[-1]
# 为所有可能的分类创建字典，如果当前的键值不存在，则扩展字典并将当前键值加入字典。每个键值都记录了当前类别出现的次数
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 # 对于label标签的占比，求出label标签的香农熵
shannonEnt = 0.0
for key in labelCounts:
# 使用所有类标签的发生频率计算类别出现的概率
prob = float(labelCounts[key])/numEntries
# 计算香农熵，以 2 为底求对数
shannonEnt -= prob * log(prob, 2)
# -----------计算香农熵的第一种实现方式end------------------------------------------------ # # -----------计算香农熵的第二种实现方式start--------------------------------------------
# # 统计标签出现的次数
# label_count = Counter(data[-1] for data in dataSet)
# # 计算概率
# probs = [p[1] / len(dataSet) for p in label_count.items()]
# # 计算香农熵
# shannonEnt = sum([-p * log(p, 2) for p in probs])
# # -----------计算香农熵的第二种实现方式end----------------------------------------------
return shannonEnt
3. 按照给定特征划分数据集
将给定特征的特征值等于value的行剩下列作为子数据集
def splitDataSet(dataSet, index, value):
"""
Desc：
划分数据集
splitDataSet(通过遍历dataSet数据集，求出index对应的colnum列的值为value的行)
就是依据index列进行分类，如果index列的数据等于 value的时候，就要将 index 划分到我们创建的新的数据集中
Args:
dataSet -- 数据集 带划分的数据集
index -- 表示每行的index列 划分数据集的特征
value -- 表示index列对应的value值 需要返回的特征的值
Returns:
index 列为 value 的数据集【该数据集需要排除index列】
"""
# -----------切分数据集的第一种方式 start------------------------------------
retDataSet = []
for featVec in dataSet:
# index列为value的数据集【该数据集需要排除index列】
# 判断index列的值是否为value
if featVec[index] == value:
# chop out index used for splitting
# [:index]表示前index行，即若 index 为2，就是取 featVec 的前 index 行
reduceFeatVec = featVec[:index]
reduceFeatVec.extend(featVec[index+1:])
# [index+1:]表示从跳过 index 的 index+1行，取接下来的数据
# 收集结果值 index列为value的行【该行需要排除index列】
retDataSet.append(reduceFeatVec)
# -----------切分数据集的第一种方式 end------------------------------------
# # -----------切分数据集的第二种方式 start------------------------------------
# retDataSet = [data[:index] + data[index + 1:] for data in dataSet for i, v in enumerate(data) if i == index and v == value]
# # -----------切分数据集的第二种方式 end------------------------------------
return retDataSet
4. 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
"""
Desc:
选择切分数据集的最佳特征
Args:
dataSet -- 需要切分的数据集
Returns:
bestFeature -- 切分数据集的最优的特征列
"""
# 求第一行有多少列的 Feature, 最后一列是label列嘛
numFeatures = len(dataSet[0]) - 1
# label的信息熵
baseEntropy = calcShannonEnt(dataSet)
# 最优的信息增益值, 和最优的Featurn编号
bestInfoGain, bestFeature = 0.0, -1
for i in range(numFeatures):
# create a list of all the examples of this feature
# 获取每一个实例的第i+1个feature，组成list集合
featList = [example[i] for example in dataSet]
# get a set of unique values
# 获取剔重后的集合，使用set对list数据进行去重
uniqueVals = set(featList)
# 创建一个临时的信息熵
newEntropy = 0.0
# 遍历某一列的value集合，计算该列的信息熵
# 遍历当前特征中的所有唯一属性值，对每个唯一属性值划分一次数据集，计算数据集的新熵值，并对所有唯一特征值得到的熵求和
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
# gain[信息增益]: 划分数据集前后的信息变化， 获取信息熵最大的值
# 信息增益是熵的减少或者是数据无序度的减少。最后，比较所有特征中的信息增益，返回最好特征划分的索引值。
infoGain = baseEntropy - newEntropy
print('infoGain = ', 'bestFeature=', i, baseEntropy, newEntropy)
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
5. 利用operator操作键值排序字典，并返回出现次数最多的分类名称
def majorityCnt(classList):
"""
Desc:
选择出现次数最多的一个结果
Args:
classList label列的集合
Returns:
bestFeature 最优的特征列
"""
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
# 倒叙排列classCount得到一个字典集合，然后取出第一个就是结果（yes/no），即出现次数最多的结果
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
6. 创建决策树
def createTree(dataSet, labels):
"""
Desc:
创建决策树
Args:
dataSet -- 要创建决策树的训练数据集
labels -- 训练数据集中特征对应的含义的labels，不是目标变量
Returns:
myTree -- 创建完成的决策树
"""
classList = [example[-1] for example in dataSet]
# 如果数据集的最后一列的第一个值出现的次数=整个集合的数量，也就说只有一个类别，就只直接返回结果就行
# 第一个停止条件：所有的类标签完全相同，则直接返回该类标签。
# count() 函数是统计括号中的值在list中出现的次数
if classList.count(classList[0]) == len(classList):
return classList[0]
# 如果数据集只有1列，那么最初出现label次数最多的一类，作为结果
# 第二个停止条件：使用完了所有特征，仍然不能将数据集划分成仅包含唯一类别的分组。
if len(dataSet[0]) == 1:
return majorityCnt(classList) # 选择最优的列，得到最优列对应的label含义
bestFest = chooseBestFeatureToSplit(dataSet)
# 获取label的名称
bestFestLabel = labels[bestFest]
# 初始化myTree
myTree = {bestFestLabel: {}}
# 注：labels列表是可变对象，在PYTHON函数中作为参数时传址引用，能够被全局修改
# 所以这行代码导致函数外的同名变量被删除了元素，造成例句无法执行，提示'no surfacing' is not in list
del(labels[bestFest])
# 取出最优列，然后它的branch做分类
featValues = [example[bestFest] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
# 求出剩余的标签label
subLabels = labels[:]
# 遍历当前选择特征包含的所有属性值，在每个数据集划分上递归调用函数createTree()
myTree[bestFestLabel][value] = createTree(splitDataSet(dataSet, bestFest, value), subLabels)
return myTree
7. 使用决策树的分类函数
def classify(inputTree, featLabels, testVec):
"""
Desc:
对新数据进行分类
Args:
inputTree -- 已经训练好的决策树模型
featLabels -- Feature标签对应的名称，不是目标变量
testVec -- 测试输入的数据
Returns:
classLabel -- 分类的结果值，需要映射label才能知道名称
"""
# 获取tree的根节点对于的key值
firstStr = list(inputTree.keys())[0]
# 通过key得到根节点对应的value
secondDict = inputTree[firstStr]
# 判断根节点名称获取根节点在label中的先后顺序，这样就知道输入的testVec怎么开始对照树来做分类
featIndex = featLabels.index(firstStr)
# 测试数据，找到根节点对应的label位置，也就知道从输入的数据的第几位来开始分类
key = testVec[featIndex]
valueOfFeat = secondDict[key]
print('+++', firstStr, 'xxx', secondDict, '---', key, '>>>', valueOfFeat)
# 测试数据，找到根节点对应的label位置，也就知道从输入的数据的第几位来开始分类
if isinstance(valueOfFeat, dict):
classLabel=classify(valueOfFeat, featLabels, testVec)
else:
classLabel = valueOfFeat
return classLabel
8. 使用pickle模块存储决策树
def storeTree(inputTree, filename):
"""
Desc:
将之前训练好的决策树模型存储起来，使用 pickle 模块
Args:
inputTree -- 以前训练好的决策树模型
filename -- 要存储的名称
Returns:
None
"""
# -------------- 第一种方法 start --------------
fw = open(filename, 'wb')
pickle.dump(inputTree, fw)
fw.close() def grabTree(filename):
"""
Desc:
将之前存储的决策树模型使用 pickle 模块 还原出来
Args:
filename -- 之前存储决策树模型的文件名
Returns:
pickle.load(fr) -- 将之前存储的决策树模型还原出来
"""
fr = open(filename, 'rb')
return pickle.load(fr)
9. 测试模块
def fishTest():
"""
Desc:
对动物是否是鱼类分类的测试函数，并将结果使用 matplotlib 画出来
Args:
None
Returns:
None
"""
# 1.创建数据和结果标签
myDat, labels = createDataSet()
# print(myDat, labels) # 计算label分类标签的香农熵
# calcShannonEnt(myDat)
# # 求第0列 为 1/0的列的数据集【排除第0列】
# print('1---', splitDataSet(myDat, 0, 1))
# print('0---', splitDataSet(myDat, 0, 0))
# # 计算最好的信息增益的列
# print(chooseBestFeatureToSplit(myDat))
import copy
myTree = createTree(myDat, copy.deepcopy(labels))
print(myTree)
# [1, 1]表示要取的分支上的节点位置，对应的结果值
print(classify(myTree, labels, [1, 1]))
# 画图可视化展现
#dtPlot.createPlot(myTree)
createPlot(myTree)
if __name__ == "__main__":
fishTest()
10. 至此决策树就完成了，但是我们还有一个决策树绘制模块没写--决策树绘制模块
# 定义文本框 和 箭头格式 【 sawtooth 波浪方框, round4 矩形方框 , fc表示字体颜色的深浅 0.1~0.9 依次变浅，没错是变浅】
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-") def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
# 根节点开始遍历
for key in secondDict.keys():
# 判断子节点是否为dict, 不是+1
if type(secondDict[key]) is dict:
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
# 根节点开始遍历
for key in secondDict.keys():
# 判断子节点是不是dict, 求分枝的深度
# ----------写法1 start ---------------
if type(secondDict[key]) is dict:
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
# ----------写法1 end --------------- # ----------写法2 start --------------
# thisDepth = 1 + getTreeDepth(secondDict[key]) if type(secondDict[key]) is dict else 1
# ----------写法2 end --------------
# 记录最大的分支深度
maxDepth = max(maxDepth, thisDepth)
return maxDepth def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args) def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30) def plotTree(myTree, parentPt, nodeTxt):
# 获取叶子节点的数量
numLeafs = getNumLeafs(myTree)
# 获取树的深度
# depth = getTreeDepth(myTree) # 找出第1个中心点的位置，然后与 parentPt定点进行划线
cntrPt = (plotTree.xOff + (1 + numLeafs) / 2 / plotTree.totalW, plotTree.yOff)
# print(cntrPt)
# 并打印输入对应的文字
plotMidText(cntrPt, parentPt, nodeTxt) firstStr = list(myTree.keys())[0]
# 可视化Node分支点
plotNode(firstStr, cntrPt, parentPt, decisionNode)
# 根节点的值
secondDict = myTree[firstStr]
# y值 = 最高点-层数的高度[第二个节点位置]
plotTree.yOff = plotTree.yOff - 1 / plotTree.totalD
for key in secondDict.keys():
# 判断该节点是否是Node节点
if type(secondDict[key]) is dict:
# 如果是就递归调用[recursion]
plotTree(secondDict[key], cntrPt, str(key))
else:
# 如果不是，就在原来节点一半的地方找到节点的坐标
plotTree.xOff = plotTree.xOff + 1 / plotTree.totalW
# 可视化该节点位置
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
# 并打印输入对应的文字
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1 / plotTree.totalD def createPlot(inTree):
# 创建一个figure的模版
fig = plt.figure(1, facecolor='green')
fig.clf() axprops = dict(xticks=[], yticks=[])
# 表示创建一个1行，1列的图，createPlot.ax1 为第 1 个子图，
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
# 半个节点的长度
plotTree.xOff = -0.5 / plotTree.totalW
plotTree.yOff = 1.0
plotTree(inTree, (0.5, 1.0), '')
plt.show() # 测试数据集
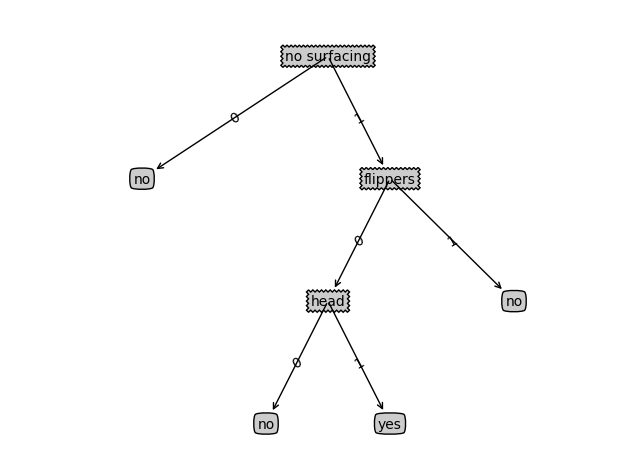
def retrieveTree(i):
listOfTrees = [
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i]
myTree = retrieveTree(1)
createPlot(myTree)
结果如下图：
全部代码如下所示：
"""
created on 2018-9-21
Updated on 2018-9-21
KNN : 决策树
"""
import matplotlib
import operator
from math import log
from collections import Counter
import pickle
import matplotlib.pyplot as plt def createDataSet():
"""
Desc:
创建数据集
Args:
无需传入参数
Returns:
返回数据集和对应的label标签
"""
# dataSet 前两列是特征，最后一列对应的是每条数据对应的分类标签
dataSet = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels def calcShannonEnt(dataSet):
"""
Desc：
calculate Shannon entropy -- 计算给定数据集的香农熵
Args:
dataSet -- 数据集
Returns:
shannonEnt -- 返回 每一组 feature 下的某个分类下，香农熵的信息期望
"""
# -----------计算香农熵的第一种实现方式start----------------------------------------------
# 求list的长度，表示计算参与训练的数据量
numEntries = len(dataSet)
# 下面输出我们测试的数据集的一些信息
# 例如：<type 'list'> numEntries: 5 是下面的代码的输出
# print(type(dataSet), 'numEntries: ', numEntries) # 计算分类标签label出现的次数
labelCounts = {}
# the the number of unique elements and their occurance
for featVec in dataSet:
# 将当前实例的标签存储，即每一行数据的最后一个数据代表的是标签
currentLabel = featVec[-1]
# 为所有可能的分类创建字典，如果当前的键值不存在，则扩展字典并将当前键值加入字典。每个键值都记录了当前类别出现的次数
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 # 对于label标签的占比，求出label标签的香农熵
shannonEnt = 0.0
for key in labelCounts:
# 使用所有类标签的发生频率计算类别出现的概率
prob = float(labelCounts[key])/numEntries
# 计算香农熵，以 2 为底求对数
shannonEnt -= prob * log(prob, 2)
# -----------计算香农熵的第一种实现方式end------------------------------------------------ # # -----------计算香农熵的第二种实现方式start--------------------------------------------
# # 统计标签出现的次数
# label_count = Counter(data[-1] for data in dataSet)
# # 计算概率
# probs = [p[1] / len(dataSet) for p in label_count.items()]
# # 计算香农熵
# shannonEnt = sum([-p * log(p, 2) for p in probs])
# # -----------计算香农熵的第二种实现方式end----------------------------------------------
return shannonEnt def splitDataSet(dataSet, index, value):
"""
Desc：
划分数据集
splitDataSet(通过遍历dataSet数据集，求出index对应的colnum列的值为value的行)
就是依据index列进行分类，如果index列的数据等于 value的时候，就要将 index 划分到我们创建的新的数据集中
Args:
dataSet -- 数据集 带划分的数据集
index -- 表示每行的index列 划分数据集的特征
value -- 表示index列对应的value值 需要返回的特征的值
Returns:
index 列为 value 的数据集【该数据集需要排除index列】
"""
# -----------切分数据集的第一种方式 start------------------------------------
retDataSet = []
for featVec in dataSet:
# index列为value的数据集【该数据集需要排除index列】
# 判断index列的值是否为value
if featVec[index] == value:
# chop out index used for splitting
# [:index]表示前index行，即若 index 为2，就是取 featVec 的前 index 行
reduceFeatVec = featVec[:index]
reduceFeatVec.extend(featVec[index+1:])
# [index+1:]表示从跳过 index 的 index+1行，取接下来的数据
# 收集结果值 index列为value的行【该行需要排除index列】
retDataSet.append(reduceFeatVec)
# -----------切分数据集的第一种方式 end------------------------------------
# # -----------切分数据集的第二种方式 start------------------------------------
# retDataSet = [data[:index] + data[index + 1:] for data in dataSet for i, v in enumerate(data) if i == index and v == value]
# # -----------切分数据集的第二种方式 end------------------------------------
return retDataSet def chooseBestFeatureToSplit(dataSet):
"""
Desc:
选择切分数据集的最佳特征
Args:
dataSet -- 需要切分的数据集
Returns:
bestFeature -- 切分数据集的最优的特征列
"""
# -----------选择最优特征的第一种方式 start------------------------------------
# 求第一行有多少列的 Feature, 最后一列是label列嘛
numFeatures = len(dataSet[0]) - 1
# label的信息熵
baseEntropy = calcShannonEnt(dataSet)
# 最优的信息增益值, 和最优的Featurn编号
bestInfoGain, bestFeature = 0.0, -1
for i in range(numFeatures):
# create a list of all the examples of this feature
# 获取每一个实例的第i+1个feature，组成list集合
featList = [example[i] for example in dataSet]
# get a set of unique values
# 获取剔重后的集合，使用set对list数据进行去重
uniqueVals = set(featList)
# 创建一个临时的信息熵
newEntropy = 0.0
# 遍历某一列的value集合，计算该列的信息熵
# 遍历当前特征中的所有唯一属性值，对每个唯一属性值划分一次数据集，计算数据集的新熵值，并对所有唯一特征值得到的熵求和
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
# gain[信息增益]: 划分数据集前后的信息变化， 获取信息熵最大的值
# 信息增益是熵的减少或者是数据无序度的减少。最后，比较所有特征中的信息增益，返回最好特征划分的索引值。
infoGain = baseEntropy - newEntropy
print('infoGain = ', 'bestFeature=', i, baseEntropy, newEntropy)
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
# -----------选择最优特征的第一种方式 end------------------------------------ # # -----------选择最优特征的第二种方式 start------------------------------------
# # 计算初始香农熵
# base_entropy = calcShannonEnt(dataSet)
# best_info_gain = 0
# best_feature = -1
# # 遍历每一个特征
# for i in range(len(dataSet[0]) - 1):
# # 对当前特征进行统计
# feature_count = Counter([data[i] for data in dataSet])
# # 计算分割后的香农熵
# new_entropy = sum(feature[1] / float(len(dataSet)) * calcShannonEnt(splitDataSet(dataSet, i, feature[0])) \
# for feature in feature_count.items())
# # 更新值
# info_gain = base_entropy - new_entropy
# print('No. {0} feature info gain is {1:.3f}'.format(i, info_gain))
# if info_gain > best_info_gain:
# best_info_gain = info_gain
# best_feature = i
# return best_feature
# # -----------选择最优特征的第二种方式 end------------------------------------ def majorityCnt(classList):
"""
Desc:
选择出现次数最多的一个结果
Args:
classList label列的集合
Returns:
bestFeature 最优的特征列
"""
# -----------majorityCnt的第一种方式 start------------------------------------
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
# 倒叙排列classCount得到一个字典集合，然后取出第一个就是结果（yes/no），即出现次数最多的结果
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
# -----------majorityCnt的第一种方式 end------------------------------------ # # -----------majorityCnt的第二种方式 start------------------------------------
# major_label = Counter(classList).most_common(1)[0]
# return major_label
# # -----------majorityCnt的第二种方式 end------------------------------------ def createTree(dataSet, labels):
"""
Desc:
创建决策树
Args:
dataSet -- 要创建决策树的训练数据集
labels -- 训练数据集中特征对应的含义的labels，不是目标变量
Returns:
myTree -- 创建完成的决策树
"""
classList = [example[-1] for example in dataSet]
# 如果数据集的最后一列的第一个值出现的次数=整个集合的数量，也就说只有一个类别，就只直接返回结果就行
# 第一个停止条件：所有的类标签完全相同，则直接返回该类标签。
# count() 函数是统计括号中的值在list中出现的次数
if classList.count(classList[0]) == len(classList):
return classList[0]
# 如果数据集只有1列，那么最初出现label次数最多的一类，作为结果
# 第二个停止条件：使用完了所有特征，仍然不能将数据集划分成仅包含唯一类别的分组。
if len(dataSet[0]) == 1:
return majorityCnt(classList) # 选择最优的列，得到最优列对应的label含义
bestFest = chooseBestFeatureToSplit(dataSet)
# 获取label的名称
bestFestLabel = labels[bestFest]
# 初始化myTree
myTree = {bestFestLabel: {}}
# 注：labels列表是可变对象，在PYTHON函数中作为参数时传址引用，能够被全局修改
# 所以这行代码导致函数外的同名变量被删除了元素，造成例句无法执行，提示'no surfacing' is not in list
del(labels[bestFest])
# 取出最优列，然后它的branch做分类
featValues = [example[bestFest] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
# 求出剩余的标签label
subLabels = labels[:]
# 遍历当前选择特征包含的所有属性值，在每个数据集划分上递归调用函数createTree()
myTree[bestFestLabel][value] = createTree(splitDataSet(dataSet, bestFest, value), subLabels)
return myTree def classify(inputTree, featLabels, testVec):
"""
Desc:
对新数据进行分类
Args:
inputTree -- 已经训练好的决策树模型
featLabels -- Feature标签对应的名称，不是目标变量
testVec -- 测试输入的数据
Returns:
classLabel -- 分类的结果值，需要映射label才能知道名称
"""
# 获取tree的根节点对于的key值
firstStr = list(inputTree.keys())[0]
# 通过key得到根节点对应的value
secondDict = inputTree[firstStr]
# 判断根节点名称获取根节点在label中的先后顺序，这样就知道输入的testVec怎么开始对照树来做分类
featIndex = featLabels.index(firstStr)
# 测试数据，找到根节点对应的label位置，也就知道从输入的数据的第几位来开始分类
key = testVec[featIndex]
valueOfFeat = secondDict[key]
print('+++', firstStr, 'xxx', secondDict, '---', key, '>>>', valueOfFeat)
# 测试数据，找到根节点对应的label位置，也就知道从输入的数据的第几位来开始分类
if isinstance(valueOfFeat, dict):
classLabel=classify(valueOfFeat, featLabels, testVec)
else:
classLabel = valueOfFeat
return classLabel def storeTree(inputTree, filename):
"""
Desc:
将之前训练好的决策树模型存储起来，使用 pickle 模块
Args:
inputTree -- 以前训练好的决策树模型
filename -- 要存储的名称
Returns:
None
"""
# -------------- 第一种方法 start --------------
fw = open(filename, 'wb')
pickle.dump(inputTree, fw)
fw.close() def grabTree(filename):
"""
Desc:
将之前存储的决策树模型使用 pickle 模块 还原出来
Args:
filename -- 之前存储决策树模型的文件名
Returns:
pickle.load(fr) -- 将之前存储的决策树模型还原出来
"""
fr = open(filename, 'rb')
return pickle.load(fr) # 定义文本框 和 箭头格式 【 sawtooth 波浪方框, round4 矩形方框 , fc表示字体颜色的深浅 0.1~0.9 依次变浅，没错是变浅】
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-") def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
# 根节点开始遍历
for key in secondDict.keys():
# 判断子节点是否为dict, 不是+1
if type(secondDict[key]) is dict:
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
# 根节点开始遍历
for key in secondDict.keys():
# 判断子节点是不是dict, 求分枝的深度
# ----------写法1 start ---------------
if type(secondDict[key]) is dict:
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
# ----------写法1 end --------------- # ----------写法2 start --------------
# thisDepth = 1 + getTreeDepth(secondDict[key]) if type(secondDict[key]) is dict else 1
# ----------写法2 end --------------
# 记录最大的分支深度
maxDepth = max(maxDepth, thisDepth)
return maxDepth def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args) def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30) def plotTree(myTree, parentPt, nodeTxt):
# 获取叶子节点的数量
numLeafs = getNumLeafs(myTree)
# 获取树的深度
# depth = getTreeDepth(myTree) # 找出第1个中心点的位置，然后与 parentPt定点进行划线
cntrPt = (plotTree.xOff + (1 + numLeafs) / 2 / plotTree.totalW, plotTree.yOff)
# print(cntrPt)
# 并打印输入对应的文字
plotMidText(cntrPt, parentPt, nodeTxt) firstStr = list(myTree.keys())[0]
# 可视化Node分支点
plotNode(firstStr, cntrPt, parentPt, decisionNode)
# 根节点的值
secondDict = myTree[firstStr]
# y值 = 最高点-层数的高度[第二个节点位置]
plotTree.yOff = plotTree.yOff - 1 / plotTree.totalD
for key in secondDict.keys():
# 判断该节点是否是Node节点
if type(secondDict[key]) is dict:
# 如果是就递归调用[recursion]
plotTree(secondDict[key], cntrPt, str(key))
else:
# 如果不是，就在原来节点一半的地方找到节点的坐标
plotTree.xOff = plotTree.xOff + 1 / plotTree.totalW
# 可视化该节点位置
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
# 并打印输入对应的文字
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1 / plotTree.totalD def createPlot(inTree):
# 创建一个figure的模版
fig = plt.figure(1, facecolor='green')
fig.clf() axprops = dict(xticks=[], yticks=[])
# 表示创建一个1行，1列的图，createPlot.ax1 为第 1 个子图，
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
# 半个节点的长度
plotTree.xOff = -0.5 / plotTree.totalW
plotTree.yOff = 1.0
plotTree(inTree, (0.5, 1.0), '')
plt.show() # # 测试画图
# def createPlot():
# fig = plt.figure(1, facecolor='white')
# fig.clf()
# # ticks for demo puropses
# createPlot.ax1 = plt.subplot(111, frameon=False)
# plotNode('a decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
# plotNode('a leaf node', (0.8, 0.1), (0.3, 0.8), leafNode)
# plt.show() # 测试数据集
def retrieveTree(i):
listOfTrees = [
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i] # myTree = retrieveTree(1)
# createPlot(myTree) def fishTest():
"""
Desc:
对动物是否是鱼类分类的测试函数，并将结果使用 matplotlib 画出来
Args:
None
Returns:
None
"""
# 1.创建数据和结果标签
myDat, labels = createDataSet()
import copy
myTree = createTree(myDat, copy.deepcopy(labels))
print(myTree)
# [1, 1]表示要取的分支上的节点位置，对应的结果值
print(classify(myTree, labels, [1, 1])) # 画图可视化展现
#dtPlot.createPlot(myTree)
createPlot(myTree) if __name__ == '__main__':
fishTest()
结果如下图：
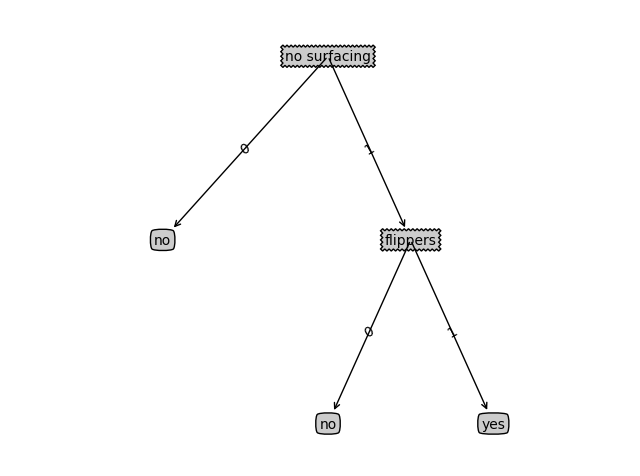
项目案例2: 使用决策树预测隐形眼镜类型
11. 隐形眼镜模块
def ContactLensesTest():
"""
Desc:
预测隐形眼镜的测试代码，并将结果画出来
Args:
none
Returns:
none
"""
# 加载隐形眼镜相关的 文本文件 数据
fr = open('lenses.txt')
# 解析数据，获得 features 数据
lenses = [inst.strip().split('\t') for inst in fr.readlines()]
# 得到数据的对应的 Labels
lensesLabels = ['age', 'prescript', 'astigmatic', 'tearRate']
# 使用上面的创建决策树的代码，构造预测隐形眼镜的决策树
lensesTree = createTree(lenses, lensesLabels)
print(lensesTree)
# 画图可视化展现
# dtPlot.createPlot(lensesTree)
createPlot(lensesTree)
if __name__ == '__main__':
#fishTest()
ContactLensesTest()
结果如下：
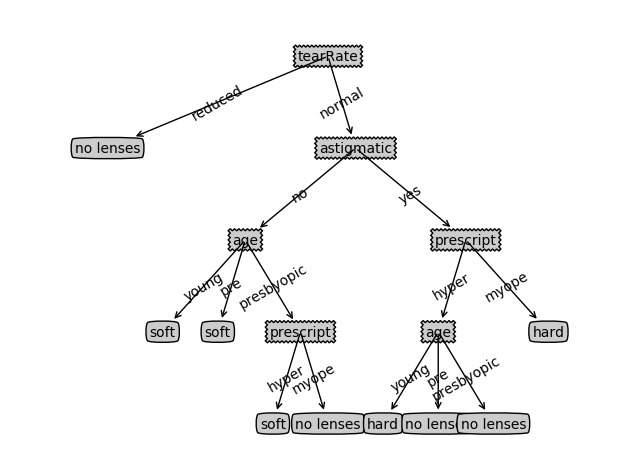
在鱼类测试模块之后添加隐形眼镜模块，main函数添加一行即可。
总共11个模块，总代码的顺序并没有一些规定，但是模块10要在模块9之前。总之，如果发现模块的顺序不太一样，调换一下就行了。让我们在AI的路上越走越远。。。
ID3算法下的决策树的更多相关文章
- 决策树ID3算法--python实现
参考: 统计学习方法>第五章决策树] http://pan.baidu.com/s/1hrTscza 决策树的python实现 有完整程序 决策树(ID3.C4.5.CART ...
- 02-21 决策树ID3算法
目录 决策树ID3算法 一.决策树ID3算法学习目标 二.决策树引入 三.决策树ID3算法详解 3.1 if-else和决策树 3.2 信息增益 四.决策树ID3算法流程 4.1 输入 4.2 输出 ...
- ID3算法（1）
1 简述1.1 id3是一种基于决策树的分类算法,由J.Ross Quinlan在1986年开发.id3根据信息增益,运用自顶向下的贪心策略建立决策树.信息增益用于度量某个属性对样本集合分类的好 ...
- 决策树 -- ID3算法小结
ID3算法(Iterative Dichotomiser 3 迭代二叉树3代),是一个由Ross Quinlan发明的用于决策树的算法:简单理论是越是小型的决策树越优于大的决策树. 算法归 ...
- 决策树-预测隐形眼镜类型 （ID3算法，C4.5算法，CART算法，GINI指数,剪枝，随机森林）
1. 1.问题的引入 2.一个实例 3.基本概念 4.ID3 5.C4.5 6.CART 7.随机森林 2. 我们应该设计什么的算法,使得计算机对贷款申请人员的申请信息自动进行分类,以决定能否贷款? ...
- 决策树笔记：使用ID3算法
决策树笔记:使用ID3算法 决策树笔记:使用ID3算法 机器学习 先说一个偶然的想法:同样的一堆节点构成的二叉树,平衡树和非平衡树的区别,可以认为是"是否按照重要度逐渐降低"的顺序 ...
- 决策树的基本ID3算法
一 ID3算法的大致思想 基本的ID3算法是通过自顶向下构造决策树来进行学习的.我们首先思考的是树的构造从哪里开始,这就涉及到选择属性进行树的构造了,那么怎样选择属性呢?为了解决这个问题,我们使用统 ...
- 【Machine Learning in Action --3】决策树ID3算法
1.简单概念描述 决策树的类型有很多,有CART.ID3和C4.5等,其中CART是基于基尼不纯度(Gini)的,这里不做详解,而ID3和C4.5都是基于信息熵的,它们两个得到的结果都是一样的,本次定 ...
- 决策树ID3算法的java实现
决策树的分类过程和人的决策过程比较相似,就是先挑“权重”最大的那个考虑,然后再往下细分.比如你去看医生,症状是流鼻涕,咳嗽等,那么医生就会根据你的流鼻涕这个权重最大的症状先认为你是感冒,接着再根据你咳 ...
随机推荐
- QR 编码原理（三）
一.日本汉字(KANJI)是两个字节表示的字符码,编码的方式是将其转换为13字节的二进制码制. 转换步骤为: 1.对于JIS值为8140(hex) 到9FFC(hex)之间字符: a)将待转换的JIS ...
- Spring Bean自动检测
1-自动检测bean 需要用到<context:component-scan> 注意:a) 需要include进来xmlns:context命名空间:base-package指的是我们要扫 ...
- 百度echarts样式开发
Echarts如何进行实例化 var a1 = null; a1= echarts.init(document.getElementById('a1')); a1.setOption({ color: ...
- Bringing Native Performance to Electron
Bringing Native Performance to Electron https://realm.io/blog/native-performance-electron-realm/ Rea ...
- Keepalived详解（三）：Keepalived基础功能应用实例【转】
Keepalived基础功能应用实例: 1.Keepalived基础HA功能演示: 在默认情况下,Keepalived可以实现对系统死机.网络异常及Keepalived本身进行监控,也就是说当系统出现 ...
- 纪念一下我对Kalman的无限崇拜之情
今天用Kalman来求线性预测模型的系数,和LMS一对比,天啦噜,我感叹了半小时．．． 和LMS需要选合适的步长,样本序列需要足够长,迭代次数需要足够多,相比,卡尔曼真是帅呆了!不需要步长!不需要蒙特 ...
- 用Openssl计算ECDSA签名
ECDSA的全名是Elliptic Curve DSA,即椭圆曲线DSA.它是Digital Signature Algorithm (DSA)应用了椭圆曲线加密算法的变种.椭圆曲线算法的原理很复杂, ...
- scp命令:远程复制粘贴文件
文章链接:https://www.cnblogs.com/webnote/p/5877920.html scp是secure copy的简写,用于在Linux下进行远程拷贝文件的命令,和它类似的命令有 ...
- python 安装mysql报错
原 安装Python mysqlclient出现“OSError: mysql_config not found”错误 2016年06月01日 12:15:11 wangtaoking1 阅读数:11 ...
- 排查linux系统是否被入侵
在日常繁琐的运维工作中,对linux服务器进行安全检查是一个非常重要的环节.今天,分享一下如何检查linux系统是否遭受了入侵? 一.是否入侵检查 1)检查系统日志 检查系统错误登陆日志,统计IP重试 ...