Dijkstra——单源最短路径

算法思想

　　①从一个源点开始，找距离它最近的点顶点v

　　②然后以顶点v为起点，去找v能到达的顶点w，即v的邻居

　　比较源点直接到 v的距离和（源点到v的距离+v到w的距离）

　　若大于后者则更新源点的到w的开销

　　③然后去掉这个顶点v，去寻找下一个到距离源点最近的顶点重复②

　　　　最后更新完所有顶点

---

算法思路

　　1.用邻接表或者一个二维数组（邻接矩阵）来存储图

　　2.设置dist存储到源点的最短距离

　　　　　known标记顶点是被处理

　　　　　path记录路径（到达该顶点的上一个顶点）

　　3.这步的实现和算法思想中描述的一样

　　4.递归显示出源点到各个顶点的路径

---

代码实现

　　下面是完整的代码实现，分别用了邻接表和邻接矩阵来存图

　　样图如下

　　

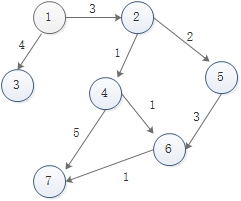
　　邻接矩阵存图

#include <iostream>
#include <cstdlib>

#define Infinity 10000
#define VERSIZE  8
#define notvertex -1

using namespace std;
typedef int  Vertex;

int dist[VERSIZE];//存储各顶点到源点的最短距离
bool S[VERSIZE];//将处理过的顶点设置为true
Vertex path[VERSIZE];//存储到该顶点的上一个顶点

void ReadGraph(int Graph[VERSIZE][VERSIZE], int m)// 边m
{
    ;
    Vertex u, v;
    int weight;
    ; i <= m; i++)
    {
        cout << "请输入第" << i << "条边:";
        cin >> u >> v;
        cout << "请输入边(" << u << "," << v << ")的权重:";
        cin >> weight;
        Graph[u][v] = weight;
    }
}

//在没处理过的顶点里 找出距离源点最近的顶点
Vertex FindMinIndex()
{
    int min = Infinity;
    Vertex min_index = ;
    ; i< VERSIZE; i++)
    {
        if (!S[i] && dist[i]<min)
        {
            min = dist[i];
            min_index = i;
        }
    }
    return min_index;
}
//算法关键
void Dijkstra(int Graph[VERSIZE][VERSIZE], Vertex source)
{
    ;
    // 初始化数组  从顶点为1开始能直接到达source的 初始化dis数组 0代表不可达
    ; i < VERSIZE; i++)
    {
        dist[i] = (Graph[source][i] ==  ? Infinity : Graph[source][i]);
        S[i] = false;
        if (dist[i] != Infinity)
            path[i] = source;
        else
            path[i] = notvertex;
    }

    //源点到自身
    dist[source] = ;
    S[source] = true;

    //循环VERSIZE-1次
    ; count < VERSIZE; count++)
    {
        Vertex u = FindMinIndex();//找出距离源点最近的顶点
        S[u] = true;//标记为已知

        ; v < VERSIZE; v++)
        {
             && !S[i])//u可达v 且 v未知
            {
                if (dist[v] >(Graph[u][v] + dist[u]))
                {
                    dist[v] = Graph[u][v] + dist[u];
                    path[v] = u;
                }
            }
        }
    }
}

void PrintDist(Vertex source)
{
    ;
    printf("Source   vertex Dist\n");
    ; i< VERSIZE; i++)
    {
        if (dist[i] != Infinity)
            printf("%d    ->    %d\t%d\n", source, i, dist[i]);
        else
            printf("%d    ->    %d\tInfinity\n", source, i);

    }
}

//输出路径
void PrintPath(int v)
{
    if (path[v] != notvertex)
    {
        PrintPath(path[v]);
        printf("--->");
    }
    printf("%d", v);
}

int main()
{
     ,j=;
    };
    ; i < VERSIZE; i++)//初始化二维数组
    {
        ; j < VERSIZE; j++)
            Graph[i][j] = ;
    }

    ReadGraph(Graph, );
    Dijkstra(Graph, );//源点是1
    PrintDist();
    printf("源点1顶点7的路径:\n");
    PrintPath();//打印从源点到顶点7的路径
    system("pause");
    ;
}

运行结果

　　

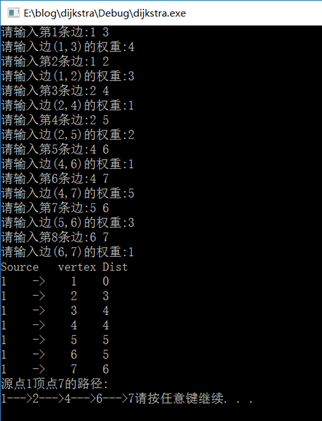
　　邻接表存图

#include <iostream>
#include <cstdlib>

#define VERSIZE 8
#define NotVertex -1
#define Infinity 100000

using namespace std;

typedef int Vertex;

typedef struct vernode VerNode;//定义顶点结构
typedef struct tablelist Table;//定义邻接表

struct vernode
{
    Vertex ver;
    int weight;//权重
    VerNode * pNext;
};

struct tablelist
{
    VerNode header;
    bool known;
    int dist;
    Vertex path;
}T[VERSIZE];

//初始化标表+读图
void InitTable(Table T[], int n, int m)//顶点数n 边数m
{
    ;
    ; i <= n; i++)//初始化表头
    {
        T[i].header.ver = i;
        T[i].header.weight = ;//到自身的权重为0
        T[i].header.pNext = NULL;
        T[i].dist = Infinity;
        T[i].known = false;
        T[i].path = NotVertex;
    }
    Vertex u, v;//边（u,v）
    ;
    VerNode * ptemp;
    ; i <= m; i++)
    {
        cout << "请输入第" << i << "条边:";
        cin >> u >> v;
        cout << "请输入边(" << u <<","<< v << ")的权重:";
        cin >> wei;
        ptemp = (VerNode*)malloc(sizeof(VerNode));
        ptemp->ver = v;
        ptemp->weight = wei;
        ptemp->pNext = T[u].header.pNext;
        T[u].header.pNext = ptemp;
    }
}

//找出到源点距离最小的顶点
Vertex FindMinIndex(Table T[], int n)
{
    ;
    int min = Infinity;
    Vertex min_index = NotVertex;
    ; i <= n; i++)
    {
        if (!T[i].known && T[i].dist < min)
        {
            min = T[i].dist;
            min_index = i;
        }
    }
    return min_index;
}

//下面是算法关键步骤啦  dijkstra算法
void Dijkstra(Table T[], int n, Vertex source)//source源点 顶点数n
{
    ;
    T[source].dist = ;//源点到源点的距离为0
    T[source].known = true;//源点已知

    //在做循环处理前 还要赋值给能直接到达源点的顶点的dist数据
    VerNode * ptemp;//能直接到达源点的顶点
    ptemp = T[source].header.pNext;
    Vertex w;
    while (ptemp)
    {
        w = ptemp->ver;
        T[w].dist = ptemp->weight;
        T[w].path = source;
        ptemp = ptemp->pNext;
    }

    Vertex v;
    //处理n-1个顶点
    ; i <= n-;i++)
    {
        //找出到源点距离最小的顶点
        v = FindMinIndex(T, n);
        if (v == NotVertex)
            break;
        T[v].known = true;
        ptemp = T[v].header.pNext;//找出顶点V所能到的顶点看是否能跟新他们的dist
        while (ptemp)
        {
            w = ptemp->ver;
            if (!T[w].known && T[w].dist > ptemp->weight + T[v].dist)//进行跟新操作
            {
                T[w].dist = ptemp->weight + T[v].dist;
                T[w].path = v;
            }
            ptemp = ptemp->pNext;
        }
    }
}

//下面输出我们的最短路径吧
void PrintPath(Table T[],Vertex v)
{
    if (T[v].path != NotVertex)
    {
        PrintPath(T, T[v].path);
        cout << " ---> ";
    }
    cout << v;
}

int main()
{
    Vertex v;
    InitTable(T, , );
    Dijkstra(T, , );
    cout << "源点1到各个顶点的最短路径如下:" << endl;
    ; v <= ; v++)
    {
        PrintPath(T, v);
        cout << endl;
    }
    system("pause");
    ;
}

运行结果

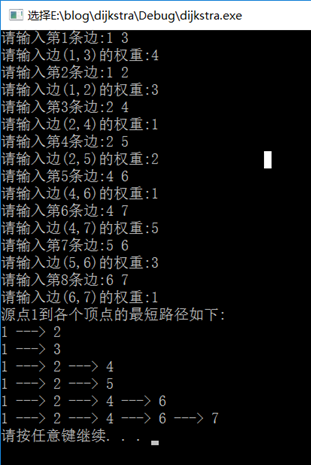
需要其他的信息可以根据需要输出

修改补充后的：SakuraOne Dijkstra单源最短路径算法

---

　　THOUGHTS

　　　　算法思想好理解  实现的话也挺好理解  但是关键就是理解的程度

　　　　学习嘛 就是不断重复的过程 对想想就对了还有多动手画画