Tree Reconstruction Gym - 101911G（构造）

---恢复内容开始---

Monocarp has drawn a tree (an undirected connected acyclic graph) and then has given each vertex an index. All indices are distinct numbers from 11 to nn . For every edge ee of this tree, Monocarp has written two numbers: the maximum indices of the vertices of the two components formed if the edge ee (and only this edge) is erased from the tree.

Monocarp has given you a list of n−1n−1 pairs of numbers. He wants you to provide an example of a tree that will produce the said list if this tree exists. If such tree does not exist, say so.

Input

The first line contains one integer nn (2≤n≤10002≤n≤1000 ) — the number of vertices in the tree.

Each of the next n−1n−1 lines contains two integers aiai and bibi each (1≤ai<bi≤n1≤ai<bi≤n ) — the maximal indices of vertices in the components formed if the ii -th edge is removed.

Output

If there is no such tree that can produce the given list of pairs, print "NO" (without quotes).

Otherwise print "YES" (without quotes) in the first line and the edges of the tree in the next n−1n−1 lines. Each of the last n−1n−1 lines should contain two integers xixi and yiyi (1≤xi,yi≤n1≤xi,yi≤n ) — vertices connected by an edge.

Note: The numeration of edges doesn't matter for this task. Your solution will be considered correct if your tree produces the same pairs as given in the input file (possibly reordered). That means that you can print the edges of the tree you reconstructed in any order.

Examples

Input

4
3 4
1 4
3 4

Output

YES
1 3
3 2
2 4

Input

3
1 3
1 3

Output

NO

Input

3
1 2
2 3

Output

NO

Note

Possible tree from the first example. Dotted lines show edges you need to remove to get appropriate pairs.

题意：就是给你n-1对点，每对点代表的是在树中隔断一条边所形成的两个不连通子树中的最大的节点（例如：隔断4-2这条边，所形成的点对为3、4），问你是否可以构造处一棵树，使其满足所给点对的要求，并输出这棵树的边！思路：我们知道不管割去哪一条边，两点对中一点是会出现n的，因为变成两个子树，n肯定会在其中一棵树中，并且大于这棵树其他节点。①给出的节点对必须包含n既然，每点对都包含n，那么我们很容易想到让n成为根节点，每次出现一个新节点，就建立一条新分支，这样就满足割去该边，得到对应点

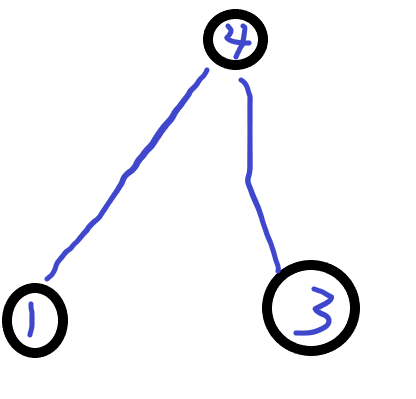但是，还有一组3、4点对，从图中知道，这应该是2节点产生的，也就是我们节点2处于3、4节点所在子树任意一个，并且为了能显示处点对3、4，这个未使用的节点2应该小于点对3、4中任意一个

②插入的节点应该小于点对中任意一个节点

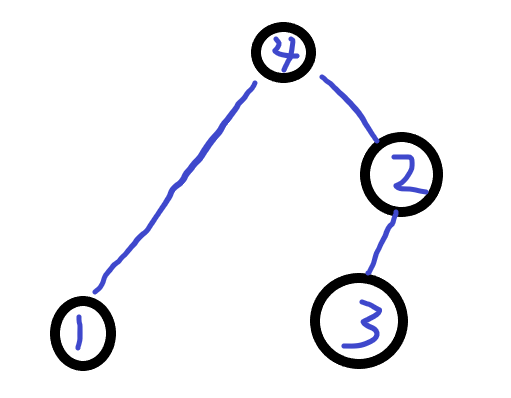
也就是说，对于出现过一次的点对，我们直接将其之间建立边；出现多次的，我们就在该点对中间插入未出现的节点；

怎么插才能保证正确性呢？所以我们选择从大到小寻找出现多次的点对，然后再该点对中也是尽量插入大的未出现的节点，也就是将大的节点尽量查到大的点对之间，如果这样还无法插入，说明无法构造这样的树。

#include<bits/stdc++.h>
using namespace std;

int n;
int vis[];
int s[];
int ll[];
int rr[];
int main()
{
    scanf("%d",&n);
    int flag = ;
    for(int i=; i<n; i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        if(a != n && b != n)
        {
            flag = ;
        }
        else if(a != n)
            vis[a]++;
        else
            vis[b]++;
    }
    int top = ;
    int cnt = ;
    if(!flag)
    {
        for(int i=; i<n; i++)
        {
            if(!vis[i])
            {
                s[++top]=i;
            }
        }
        for(int i=n-;i;i--)
        {
            if(!vis[i])continue;
            vis[i]--;
            int u = n,v;
            while(vis[i]--)
            {
                v = s[top--];
                if(v > i)
                {
                    flag = ;
                    break;
                }
                ll[++cnt] = u;
                rr[cnt] = v;
                u = v;
            }
            if(flag)break;
            ll[++cnt] = u;
            rr[cnt] = i;
        }
    }
    if(flag)printf("  NO\n");
    else
    {
        printf("YES\n");
        for(int i=;i<=cnt;i++)
        {
            printf("%d %d\n",ll[i],rr[i]);
        }
    }
}