rsa加密算法及js的JSEncrypt实现前端加密

最近的项目中用到了rsa加密算法，在实现了相关功能之后，我去了解了一下rsa相关原理，于是就写了这篇博客啦。

首先介绍一下什么是rsa加密算法：

作为非对称加密算法的老大，rsa号称是地球上最安全的加密算法。

首先了解一些数学背景（我发现我真的好喜欢看数学概念0.0），这里就不再赘诉相关数学背景了，但是请务必要理解这些概念，贴一个我觉着讲得特别清晰的概念，便于理解：

https://blog.csdn.net/u014044812/article/details/80782448

然后介绍一下rsa密钥生成过程：

1.随机选两个不等的质数p和q：

实际应用中如果这两个质数越大就越难破解

2.计算p和q的乘积n

n=p*q
n的长度就是密钥长度，然后把n写成二进制，共有多少位，这个密钥就有多少位，
在一般场景中rsa密钥一般是1024位，重要场合位2048位

3.计算n的欧拉函数φ(n)

4.随机选择一个整数e，条件是1<e<φ(n),且e与φ(n)互质

5.计算e对于φ(n)的模反元素d

ed-kφ(n)=1

（可以利用辗转相除法求的d元素，）

按照公式，d=x=-，但是一般取正整数，然后d加减φ(n)的n倍都是e的模反元素

所以取d=d+kφ(n)=-+1x3120=

6.将n和e封装成公钥，n和d封装成私钥

公钥：（n,e）

私钥：（n，d）

利用JSEncrypt实现的整个加密过程，具体实现可以看看

https://github.com/travist/jsencrypt

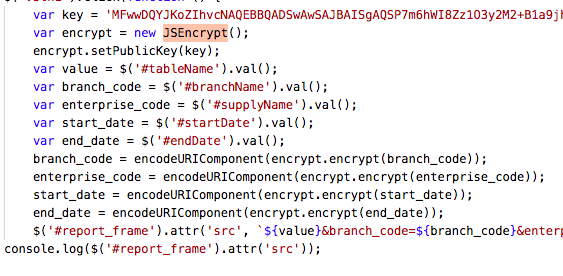
我司现在后端用java实现的解密过程，我现在在前端实现加密过程，列举部分代码