排序算法（Gif动图演示）

冒牌排序（BubbleSort）

冒泡排序是一种比较简单的排序算法，它循环走过需要排序的元素，依次比较相邻的两个元素，如果顺序错误就交换，直至没有元素交换，完成排序。

若对n个人进行排序，我们需要n-1次比较，所以第k次比较需要进行n-k次比较。排序算法通过以数据对象的两两比较作为关键，所以可以得出，冒泡排序需要进行的

比较次数为：(n-1) + (n-2) + ... + 1 = n*(n-1) / 2，因此冒泡排序的时间复杂度为O(n^2)。

算法简介:

       1.比较相邻的元素，前一个比后一个大（或者前一个比后一个小）调换位置

       2.每一对相邻的元素进行重复的工作，从开始对一直到结尾对，这步完成后，结尾为做大或最小的数.

       3.针对除了最后一个元素重复进行上面的步骤。

       4.重复1-3步骤直到完成排序

动画演示：

 

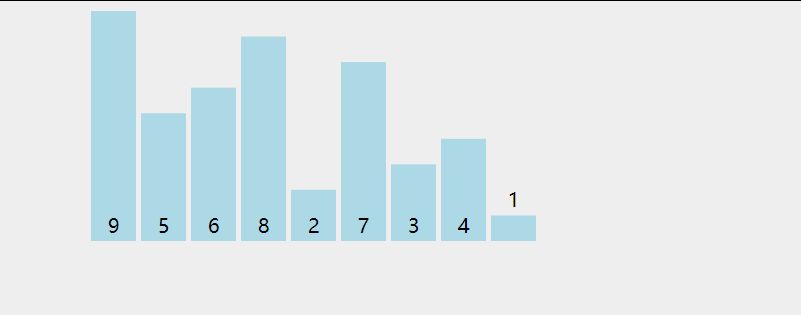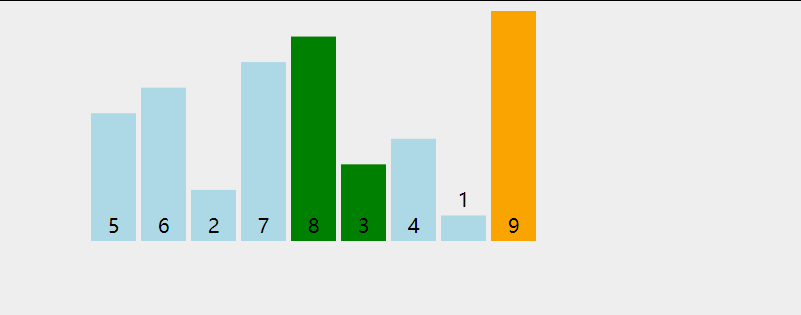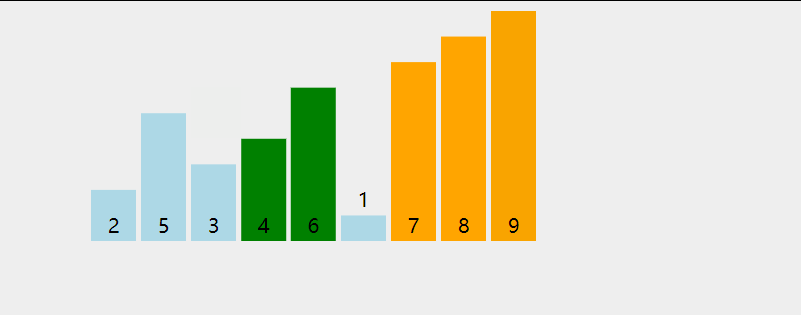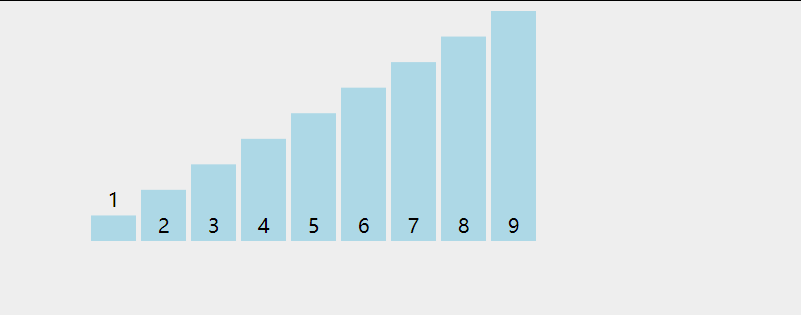
 代码如下

#include<stdio.h>
void BuddleSort(int a[],int n){
     
    for(int i=0;i<n-1;i++){
        for( int j=0;j<n-i-1;j++){
            if(a[j]>a[j+1]){
                int swap=a[j];
                a[j]=a[j+1];
                a[j+1]=swap;
            }
        }
    }
} 
int main(){
    int a[]={6, 9，8，4，5，2，1，3，7};
    int n=sizeof(a)/sizeof(int);
    BuddleSort(a,n);
    printf("冒泡排序结果：");
    
    for (int i = 0; i < n; i++)
    {
        printf("%d ", a[i]);
    }
    return 0;
}

冒牌排序改进版：鸡尾酒排序

鸡尾酒排序：又名为定向冒泡排序，相比较于传统的冒泡排序改进方法就是加入一个标志性变量exchange，用于标志某次排序过程中

是否由数据交换，若某一次排序没有进行数据交换，则说明数据已经排列好，可以立刻结束排序，避免不必要的后续比较过程，从而提高性能。

算法描述：每次排序进行正向和反向冒泡一次得到两个终值(最大值和最小值)。

代码如下

#include<stdio.h>
void BuddleSort(int a[],int n)
{
    int left=0;   //设置变量初始值 
    int right=n-1;
    int swap,j;
    while(left<right){
        for(j=left;j<right;j++)//正向冒泡，找出最大值 
        {
            if(a[j]>a[j+1])
            {
                swap=a[j];
                a[j]=a[j+1];
                a[j+1]=swap;
            } 
        }
            right--; //前移一位
        for(int j=right;j>left;j--)//反向冒泡找出最小值 
        {
            if(a[j-1]>a[j])
            {
                swap=a[j];
                a[j]=a[j-1];
                a[j-1]=swap;
            }
        }
        left++; //修改left值。后移一位 
    }
}
int main()
{
    int a[]={7,8,4,2,9,5,6,1,3};
    int n=sizeof(a)/sizeof(int);
    BuddleSort(a,n);
     printf("鸡尾酒排序结果：");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
    return 0;
 } 

 选择排序(SelectSort)

选择排序是一种简单直观的排序算法，工作原理为：在未排序的序列中找出最小(大)元素与第一个位置的元素交换位置

注意选择排序与冒泡排序的区别：冒泡排序通过依次交换相邻两个顺序不合法的元素位置，从而将当前最小（大）元素放到合适的位置；而选择排序每遍历一次都记住了当前最小（大）元素的位置，最后仅需一次交换操作即可将其放到合适的位置。

然后在剩下的元素中再找最小(大)元素与第二个元素的位置交换，依此类推，直到所有元素排序排序完成。根据上述描述，一共进行n-1趟比较后，就能完成整个排队过程。我们可以知道，第k趟比较需要进行的数组元素的两两比较的次数为n-k次，所以共需要的比较次数为n*(n-1) / 2，因此选择排序算法的时间复杂度与冒泡排序一样，也为O(n^2)。

算法简介：

     1.初始状态：序列为无序状态。

     2.第1次排序：从n个元素中找出最小(大)元素与第1个记录交换

     3.第2次排序：从n-1个元素中找出最小(大)元素与第2个记录交换

     4.第i次排序：从n-i+1个元素中找出最小(大)元素与第i个记录交换

    5.以此类推直到排序完成

动画演示：

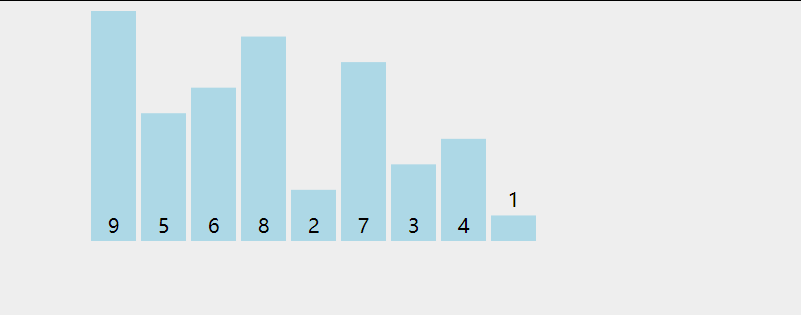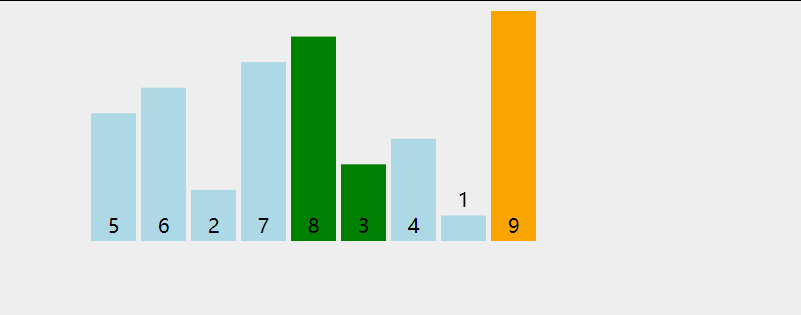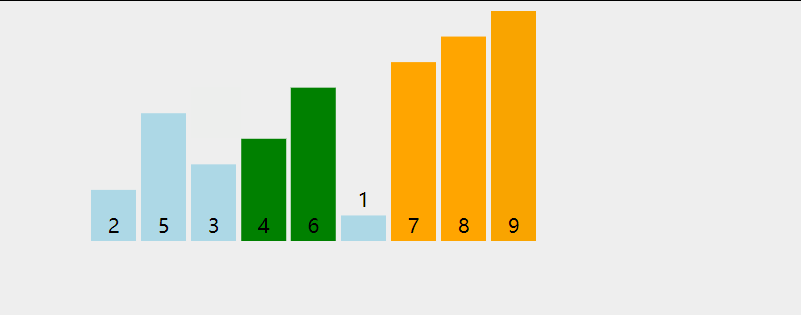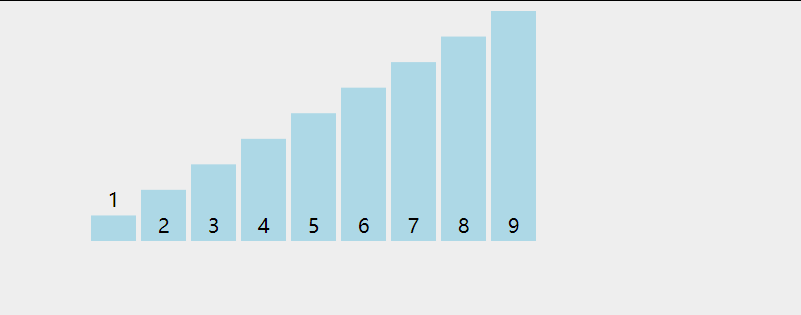
代码如下

#include<stdio.h>
void SelectSort(int a[],int n)
{
    for(int i=0;i<n-1;i++)
    {
        int min=i;  //存放数组最小值的位置 
        
        for(int j=i+1;j<n;j++)
        {
            if(a[j]<a[min]){
                min=j;   //找出最小值，并记录位置 
            }
         } 
         if(min!=i) //最小元素与第i个元素互换位置 
         {
            int swap=a[min];
             a[min]=a[i];
             a[i]=swap;
         }
    }
}
int main()
{
    int a[]={8,9,7,1,5,4,2,3,6};
    int n=sizeof(a)/sizeof(int);
    SelectSort(a,n);
     printf("选择排序结果：");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
    return 0;
}

 插入排序(InsertSort)

插入排序是一种简单直观的排序算法，工作原理为构建有序序列，对于未排序元素，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间，直到排序完成，如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。理解了插入排序的思想后，我们便能够得到它的时间复杂度。对于n个元素，一共需要进行n-1轮比较，而第k轮比较需要进行k次数组元素的两两比较，因此共需要进行的比较次数为：1 + 2 + ... + (n-1)，所以插入排序的时间复杂度同冒泡排序一样，也为O(n^2)。

算法简介：

     1.从第一个元素开始，该元素可认为已排序。

     2.取出下一个元素，在排序好的元素序列中从后往前扫描

     3.如果元素(已排序)大于新元素，将该元素移到下一位置

     4.重复3.直到找到已排序的元素小于或等于新元素的位置

     5.将新元素插入该位置后

     6.重复2-5直到排序完成

动画演示：

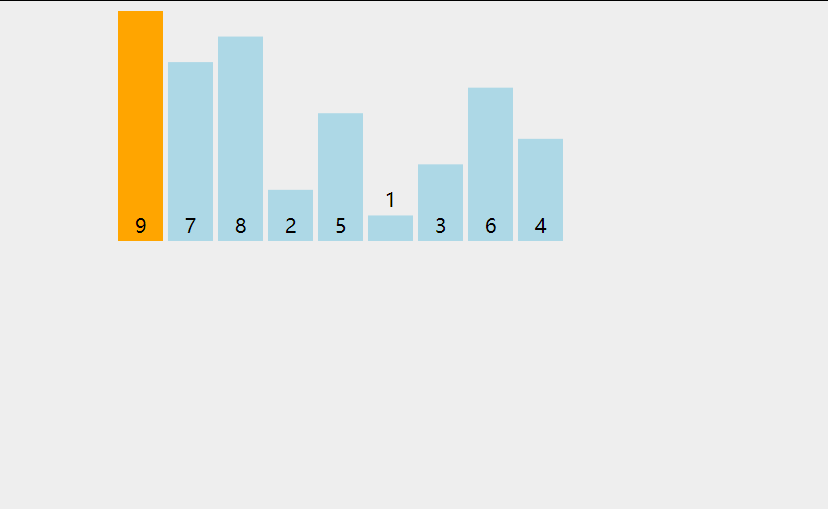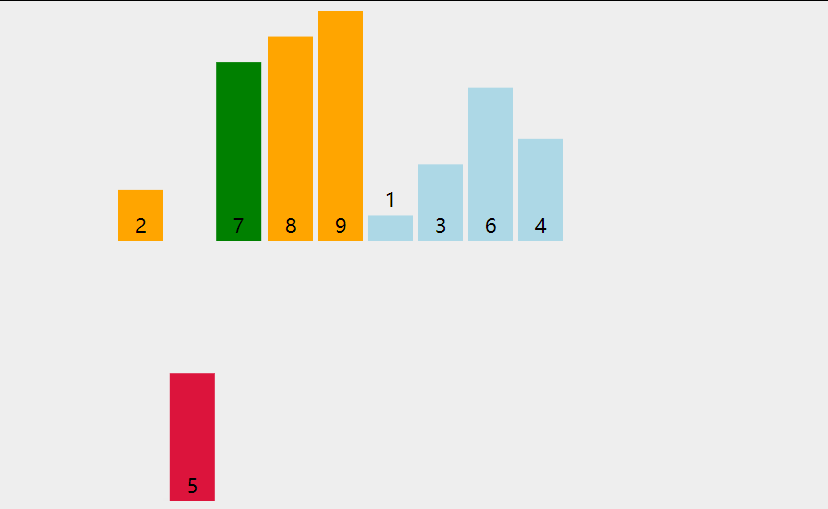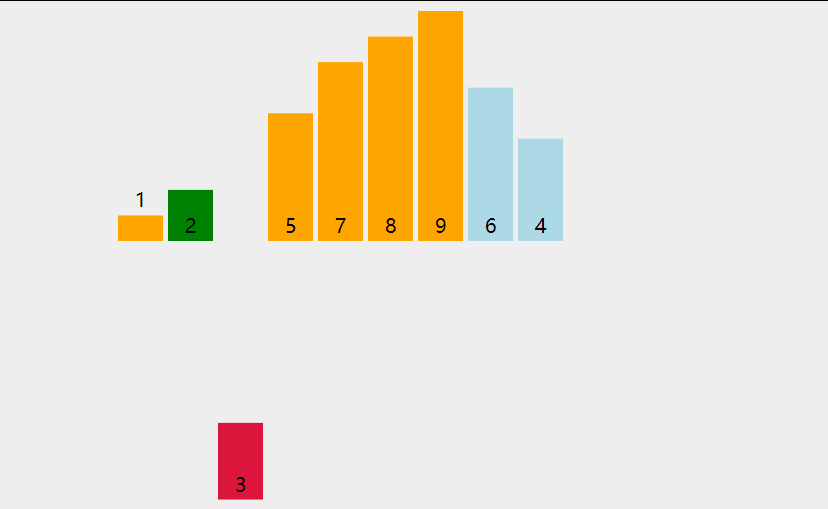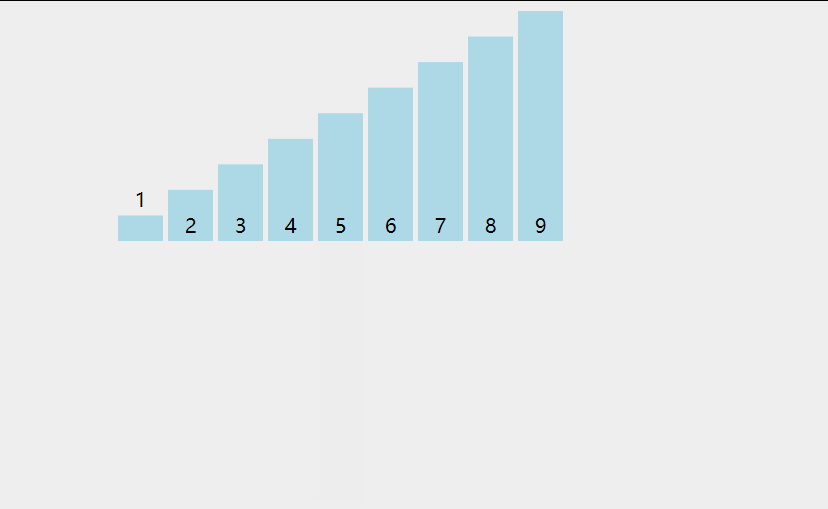
代码如下

#include<stdio.h>
void InsertSort(int a[],int n)
{
    for(int i=0;i<n;i++)
    {
        int j=i-1;
        if(a[i]<a[i-1]){ //若第i个元素小于第i-1个元素,移动有序序列插入------大于的话则直接插入 
        int swap=a[i];  //存储将要排序的元素 
        a[i]=a[i-1];   //向后移动一个元素 
        while(swap<a[j])//查询将要插入的位置 
        {
            a[j+1]=a[j];
            j--;       //元素后移 
        }
        a[j+1]=swap;//循环结束 插入到指定位置 
    }    
    }
}
int main() {
    int a[] = { 9,7,8,2,5,1,3,6,4};
    int n = sizeof(a)/sizeof(int);
    InsertSort(a, n);
    printf("排序好的数组为：");
    for (int i = 0; i < n; i++) {
        printf(" %d", a[i]);
    }
    printf("\n");
    return 0;
}

还有几种经典的排序算法没有写出，后续将补充，有不足之处还请指出。谢谢