面嚮對象程序設計第一單元作業——OO初試

一、三次作业情况简介

　　第一次：本次作业仅涉及简单的常数和幂函数的加减法。要求在正确输入下给出正确的求导结果，对错误输出报错

　　第二次：本次作业涉及常数、幂函数和标准正余弦函数的相乘和相加减，难度较上回作业有所增加。同样要求在正确输入下给出正确的求导结果，对错误输出报错。

　　第三次：本次作业涉及常数、幂函数、正余弦函数和括号表达式的相乘和相加减，难度超过前两次作业之和。同样要求在正确输入下给出正确的求导结果，对错误输出报错。

二、三次作业讨论

I.第一次作业

1.一定要提的代码风格

　　今年恰逢OO改革。正所谓“人逢喜事精神爽”，碰上第一次代码风格检查确实上来就给了我一个下马威——首次提交代码风格0分。仔细研究了一下扣分项，粗浅算下来应该是扣了有超过400分（还好没有负分）。自以为一套可行的代码风格被现实打得支离破碎。

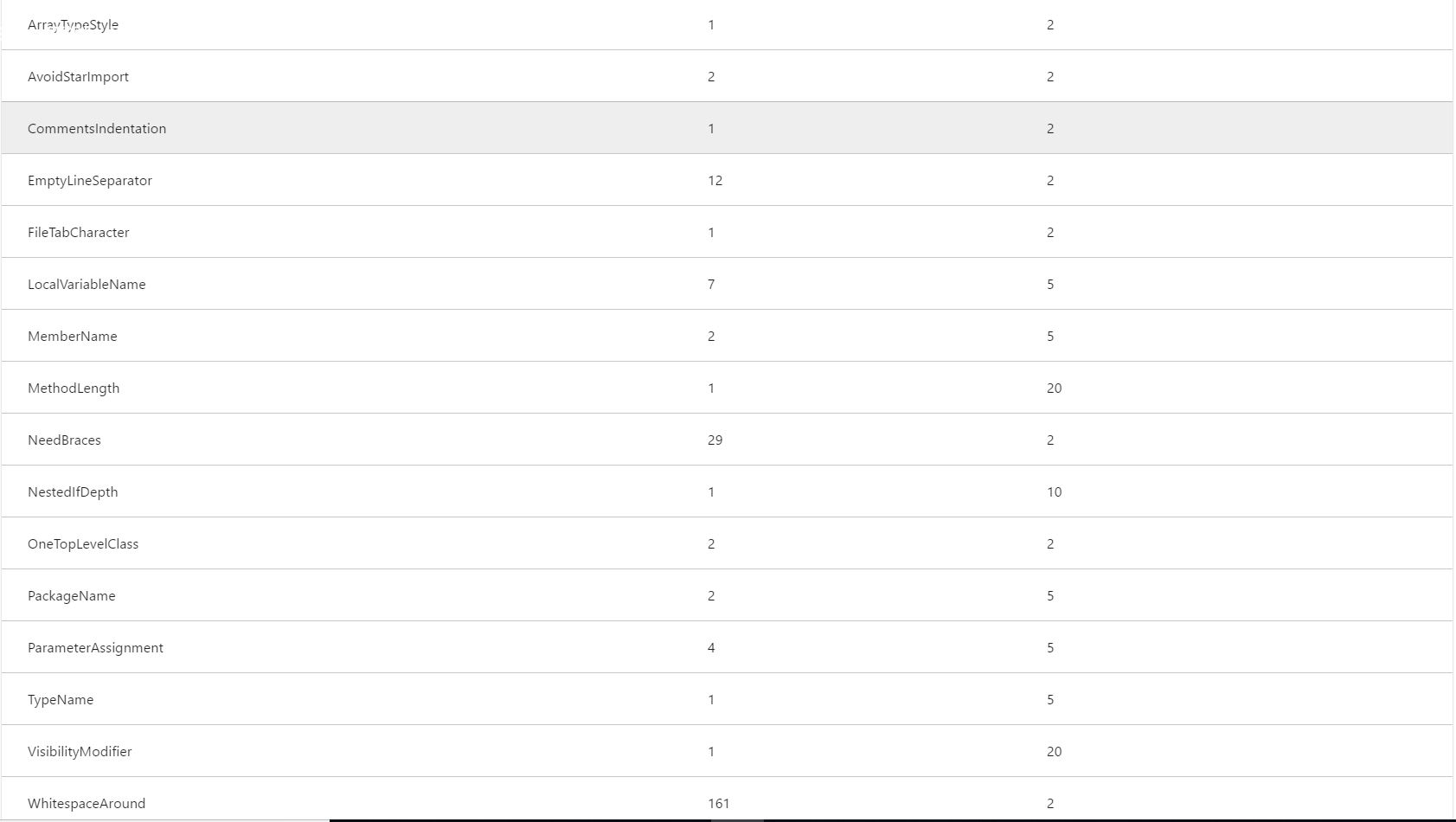
　　然而做人心态一定要好，始终坚信“方法总比问题多”的道理来解决问题。之后花了数个小时修改自己的代码风格。之后就在后两次形成了很大的改观：自己就会自觉地想到把代码写成符合格式要求的形式。确实是比之前的要赏心悦目一些（虽然没改之前对自己自信满满）。而且代码风格带来的另一个好处是——代码分工的明确化：由于有对于单个方法60行的长度要求，因此不得不想尽一切方法把很长的方法缩短，这样就需要把代码切割，任务和功能细化交给不同的方法实现，而上层部分只负责调控。这样的好处非常明显，在第三次作业debug的时候，可以更轻松地定位到自己代码的出错点，而且可以避免因阅读长代码导致的疲倦。

　　总而言之，代码风格并没有在写代码时造成不便，而且为后续的调试工作减轻了很多压力。

2.共性问题

　　Java的库提供了一些很好用的工具，比如BigInteger和ArrayList等。之前各种课程的代码是没有这么好用的工具的。如果自己重新封装这些类，又将会浪费很多不必要的时间，“工欲善其事必先利其器”，有这些好用的工具还是可以借用的。

　　此外本次的作业涉及正则表达式的概念。很多同学之前没有接触过，可能一下子难以接受，使用起来也比较费劲。我之前学习正则表达式的时候也遇到了很大的困难，这种形式化的语言的高度抽象性确实不甚平易近人，不过掌握之后确实是及其强大的工具。我个人觉得学习正则的方法在于，多利用各种实例和其对应的正则来学习，比如说URL，普通的密码等，都可以帮助了解最基本的正则的使用原理；此外还有平心静气，一味求快反而会导致更不愿意阅读，从而产生畏难情绪。

3.个性问题

　　之前提到了方法过长的问题。我的作业的主方法就涉及过长的问题，而且做了数次修改才勉强控制在60行之内。现在看来是功能所属不明晰，同类功能置于不同的地方处理，使代码的整体性和可读性较低，也使得划分困难。这一点在之后的作业变难之后得到了解决。

4.面向对象的思想

　　因为第一次写一个有一定功能的Java程序，确实在一些方面还是有面向过程的思想（比如上一个section提到的方法划分的问题，由于缺乏整体设计和类封装的思想，使得一些partition不尽人意）。本次作业的数据封装是比较重要的，体现了很好的面向对象的思想，每个对象运用自己的方法管控自己的数据。

II.第二次作业

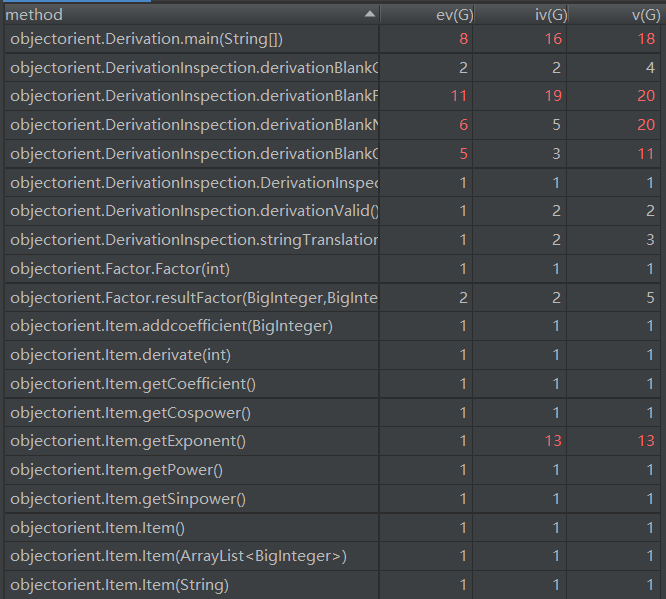
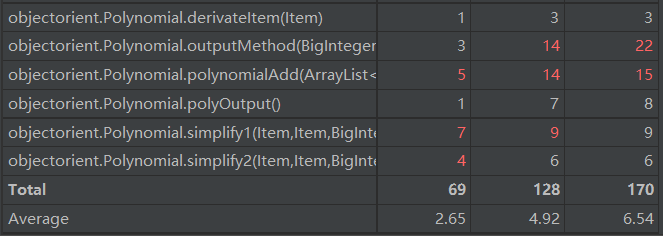
1.共性问题

　　本次的化简可以说是比较大的问题。化简涉及到三种模式：sin(x)^2 + cos(x)^2 = 1、1 - cos(x)^2 = sin(x)^2和1 - sin(x)^2 = cos(x)^2。采用何种merge方式会对作业的化简造成影响。我个人的方式是对每一项求完导即加入多项式中，因而很容易出现merge不能的情况。Merge的另一个问题是，可能merge之后相较于原来的长度更长，因而merge的判断又是一个比较challenging的问题。不过根据测试样例来看，merge的都是系数部分和幂函数部分完全相同的项。这里我个人的问题就体现出来：一次性merge操作不能保证合并同类项之后还可以进行三角函数的化简。

　　本次作业的另一个扩展是正则表达式的匹配难度又一次增加。不过对于了解一定正则表达式的同学来说并非难事。

2.个性问题

　　由于发现第一次和第二次作业的区别比较大，使得代码重构的部分很多，因此在本次的代码中开拓了多一点的类，以备后续的扩展。

　　可以从matrix看出，我的一些方法的长度控制还是不当。这大概也是学问吧，需要以后慢慢在实践当中继续学习。

III.第三次作业

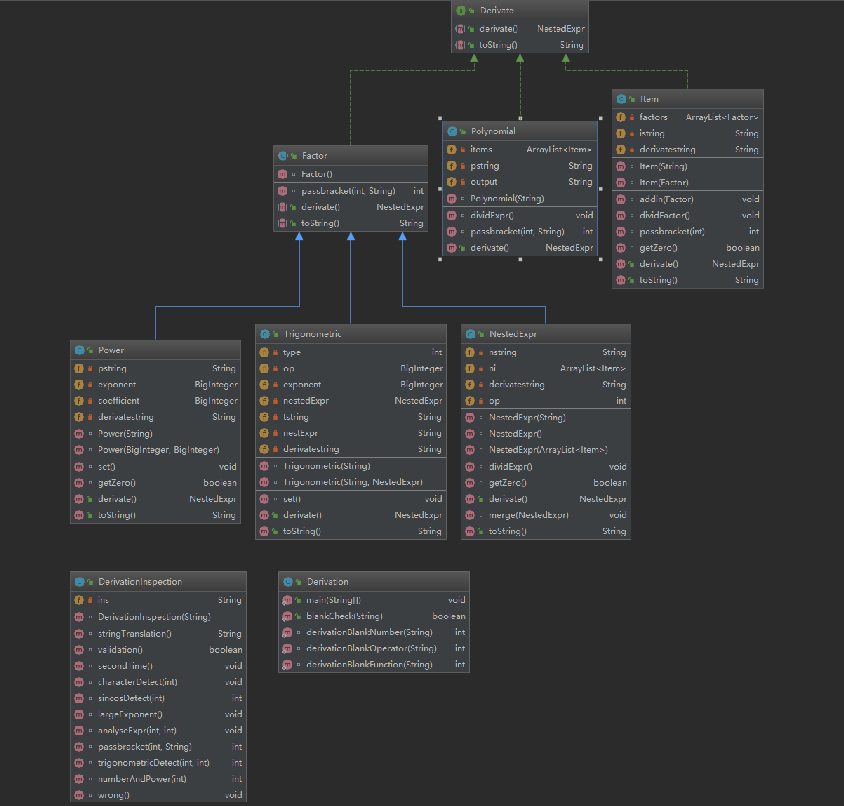
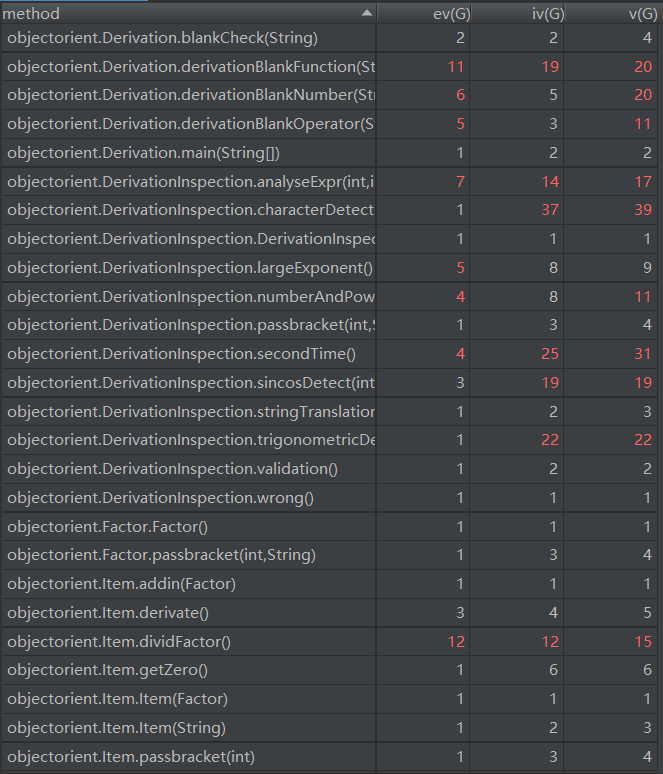
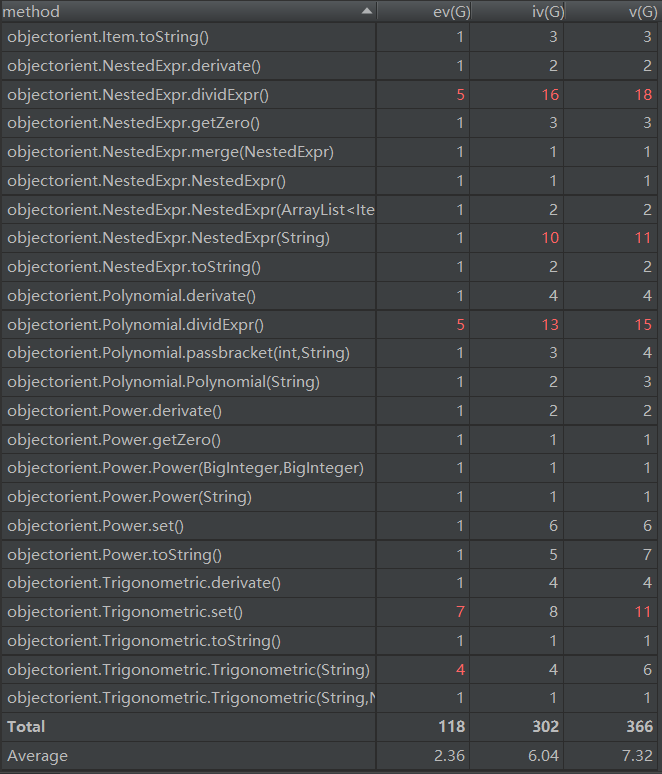
1.共性问题

　　本次OO作业的难度可以说是很不小了。本次OO作业的难度可以说是很不小了。本次OO作业的难度可以说是很不小了。（重要的事情说三遍）

　　首先是Regex的失效。有限次的正则表达式无法匹配可以无穷嵌套的括号（虽说理论上最长60个字符，可以赌一把深度，但必将导致Regex的极其複雜，複雜，複雜）。因此采用编译中的方法CFG（Context Free Grammar），或者是与其等效的DFA。在读入字符串并做了基于前两次作业要求的检测之后，对第三次作业的内容进行检查。必须出现递归嵌套的是三角函数（记sin(x)和cos(x)为标准三角函数，标准三角函数和标准三角函数以外的三角函数统称为三角函数）和表达式因子（这个名称参见指导书），而且此处的情况是，必须分别讨论括号后是否允许接入^。我个人的处理是采用了trigonometricDetect和analyseExpr两个方法分别检查三角函数内部嵌套问题和表达式因子问题，其它的普通检查不再赘述。一旦读入sin或cos，则进入trigonometricDetect部分，检测括号内是否只有单项：如果是数字和x，在正确的情况下不做任何处理；如果是三角函数或表达式因子，则分别调用trigonometricDetect和analyseExpr进行分析；在处理结束整个三角函数后，跳到该三角函数的回括号的后一个字符（如果存在的话）。一旦读入括号，执行analyseExpr。三角函数的括号与普通括号不会干扰，因为三角函数的括号会被跳过处理，而后续再匹配时已经跳过了整个三角函数。

　　其次是表达式的拆分。不过表达式的拆分与上面表达式检测的原理相似，不再赘述。

　　最后是求导和返回。由于求导项的複雜，可能产生多个项，而这些项必须再利用ArrayList管理。最后打印输出时也采用调用的方法，不过本轮利用树的性质较之前稍微明显（之前是构建树，现在是将一棵成型的树翻译出来）。

　　附加问题是化简。不过鉴于个人能力有限，处理好正确性问题已经占去了我很多时间，必须认识到自己和dalao的差距。

2.个性问题

　　这回的运气没有前两回好，在强测中被爆了一个点。后来检查的时候发现是很小的问题，稍作修改即可完成。

3.面向对象的思想

　　这回面向对象思想很强的是继承和接口的使用。设定父类和接口可以帮助统一管理，更清晰地规划代码结构，并明确各类之间的关系。私以为《Thinking in Java》可以提供一些不错的帮助。

三、一些思考

　　三次作业下来发现自己的很多不足，比如代码的架构设计——可扩展性比较差。

　　此外还有测试集的构造，并没有采用一套methodology，才会导致后面问题的出现。只能说“世事洞明皆学问”吧，自己还有很大的长进空间。

　　当然，第三回作业也提升了我的抗压能力。认识到“中华民族的伟大复兴不是轻轻松松、敲锣打鼓就能实现的”，还是要“以坚如磐石的信心、只争朝夕的劲头、坚韧不拔的毅力，一步一个脚印把前无古人的伟大事业推向前进”（意思就是这么个意思）。以我个人的水平想随随意意做好第三次作业无异于痴人说梦，在学习的同时提升自己各方面的能力，也是OO这门课程能带给我的宝贵财富吧。

---