醉汉随机行走/随机漫步问题（Random Walk Randomized Algorithm Python）

世界上有些问题看似是随机的（stochastic），没有规律可循，但很可能是人类还未发现和掌握这类事件的规律，所以说它们是随机发生的。

随机漫步（Random  Walk）是一种解决随机问题的方法，它与人类生活息息相关，例如醉汉行走的轨迹、布朗运动（Brownian Motion）、股票的涨跌等都可以用它来模拟。随机漫步已经应用到数学，物理，生物学，医学，经济等领域。

假设某地有一个醉汉，每一秒钟会朝“东”，“南”，“西”，“北”中的一个方向走一步，那么这个醉汉在走了500步之后会在什么地方？1000步呢？是不是随着时间的增长，醉汉离原点越来越远呢？这个问题看似很随机，无法解决，但是如果用电脑程序来模拟，那么就可以很容易地把醉汉行走的轨迹，醉汉离原点的距离展现出来。

解决思路：

设计四个class，分别是：Location（表示醉汉所在的位置），Direction（表示醉汉行走的方向，如果要增加或修改方向，在这个class中修改即可），Field（表示一个醉汉所在的平面区域，如果要增加醉汉的数量，在这个class中修改即可），Drunk（表示醉汉本身）

代码如下：

import math, random, pylab

class Location:
    def __init__(self,x,y):  #定义醉汉的位置，即平面上的一点，用x和y坐标表示
        self.x=x
        self.y=y
    def move(self,xc,yc):  #输入x和y坐标的变动值，返回变动后的坐标
        return Location(self.x+xc,self.y+yc)
    def getLocation(self):
        return self.x,self.y
    def getDistance(self,other):  #输入另一个点的坐标，根据x轴和y轴变动的距离，算出原点和另一个点之间的直线距离
        ox,oy=other.getLocation()
        xDist=ox-self.x
        yDist=oy-self.y
        return math.sqrt(xDist**2+yDist**2)

class Direction:
    possibleDirection=("S","W","E","N")  #可能的四种方向
    def __init__(self,direc):  #定义方向，如果此方向不在可能的四种方向里面，那么报错
        if direc in self.possibleDirection:
            self.direc=direc
        else:
            raise ValueError("in direction:__init__")
    def move(self,dist):  #输入移动距离，根据不同的方向返回平面距离
        if self.direc=="S": return (0,-dist)
        if self.direc=="W": return (-dist,0)
        if self.direc=="E": return (dist,0)
        if self.direc=="N": return (0,dist)
        else: raise ValueError("in direction: move")

class Field:
    def __init__(self,drunk,loc):  #定义醉汉和其所在的平面
        self.drunk=drunk
        self.loc=loc
    def move(self,direc,dist):  #输入方向和移动距离，获得x和y坐标的变动值，在原点上移动该值，获得变动后的坐标
        oldLoc=self.loc
        xc,yc=direc.move(dist)
        self.loc=oldLoc.move(xc,yc)
    def getLocation(self):
        return self.loc
    def getDrunk(self):
        return self.drunk

class Drunk:
    def __init__(self,name):
        self.name=name
    def move(self,field,step=1):
        if field.getDrunk()!=self:
            raise ValueError("No such drunk is found on the field")
        for i in range(step):
            direc=Direction(random.choice(Direction.possibleDirection))
            field.move(direc,1)

def performTrial(step,f):
    startLoc=f.getLocation()
    distances=[0]
    for t in range(1,step+1):
        f.getDrunk().move(f)
        newLoc=f.getLocation()
        distance=newLoc.getDistance(startLoc)
        distances.append(distance)
    return distances

drunk=Drunk("Baichi")
for i in range(3):
    f=Field(drunk,Location(0,0))
    distances=performTrial(500,f)
    pylab.plot(distances)
pylab.title("Baichi Walk")
pylab.xlabel("Time")
pylab.ylabel("Distance")
pylab.show()

运行结果如下：

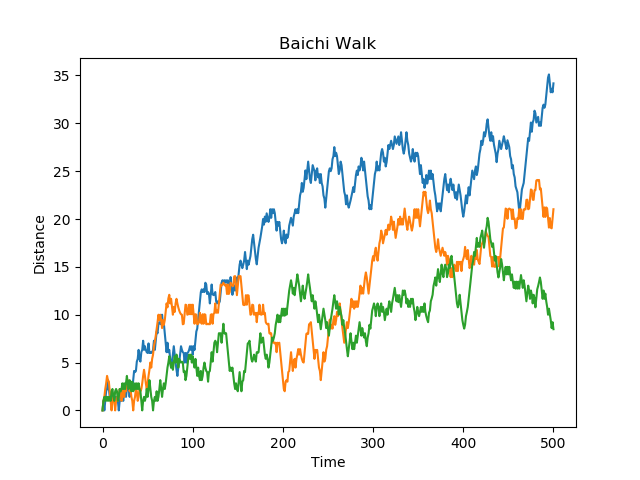
可以看出，随着时间的推移，醉汉离原点越来越远。

人们通常想当然地以为醉汉随机朝四种方向行走，来来回回，兜兜转转，估计最后还是走到离原点不远的地方。但其实醉汉每走一步，之前的基点都会随之变化。（走第一步时，100%的几率会离原点更远；走第二步时，75%的几率会离原点更远，只有25%的几率会回到原点。这就是因为走第一步时，基点是原点，而走第二步时，基点变成了走完第一步后所在的点。）

在现实生活中，假如有一天你的股票大跌，这意味着你想要收回成本的可能性就很低了。因为基点已经被拉低。。。（啊啊啊啊。。。不要告诉我这个惨痛的事实啊！！！）

参考：麻省理工学院公开课：计算机科学及编程导论（第17集）