Expectation Maximization-EM(期望最大化)-算法以及源码

在统计计算中，最大期望（EM）算法是在概率（probabilistic）模型中寻找参数最大似然估计的算法，其中概率模型依赖于无法观测的隐藏变量（Latent Variable）。最大期望经常用在机器学习和计算机视觉的数据聚类（Data Clustering） 领域。最大期望算法经过两个步骤交替进行计算，第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值；第二步是最大化（M），最大 化在 E 步上求得的最大似然值来计算参数的值。M 步上找到的参数估计值被用于下一个 E 步计算中，这个过程不断交替进行。

最大期望值算法由 Arthur Dempster,Nan Laird和Donald Rubin在他们1977年发表的经典论文中提出。他们指出此方法之前其实已经被很多作者"在他们特定的研究领域中多次提出过"。

我们用 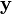 表示能够观察到的不完整的变量值，用  表示无法观察到的变量值，这样  和 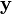 一起组成了完整的数据。 可能是实际测量丢失的数据，也可能是能够简化问题的隐藏变量，如果它的值能够知道的话。例如，在混合模型（Mixture Model）中，如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利（参见下面的例子）。

估计无法观测的数据

让  代表矢量 θ: 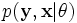 定义的参数的全部数据的概率分布（连续情况下）或者概率聚类函数（离散情况下），那么从这个函数就可以得到全部数据的最大似然值，另外，在给定的观察到的数据条件下未知数据的条件分布可以表示为：

EM算法有这么两个步骤E和M:

Expectation step: Choose q to maximize F:

Maximization step: Choose θ to maximize F:

举个例子吧：高斯混合

假设 x = (x₁,x₂,…,x_n) 是一个独立的观测样本，来自两个多元d维正态分布的混合, 让z=(z₁,z₂,…,z_n)是潜在变量，确定其中的组成部分，是观测的来源.

即：

 and 

where

 and 

目标呢就是估计下面这些参数了，包括混合的参数以及高斯的均值很方差:

似然函数:

where  是一个指示函数 ，f 是 一个多元正态分布的概率密度函数. 可以写成指数形式:

下面就进入两个大步骤了：

E-step

给定目前的参数估计 θ^(t),  Z_i 的条件概率分布是由贝叶斯理论得出，高斯之间用参数 τ加权:

.

因此，E步骤的结果:

M步骤

Q(θ|θ^(t))的二次型表示可以使得 最大化θ相对简单.  τ, (μ₁,Σ₁) and (μ₂,Σ₂) 可以单独的进行最大化.

首先考虑 τ, 有条件τ₁ + τ₂=1:

和MLE的形式是类似的，二项分布 , 因此:

下一步估计 (μ₁,Σ₁):

和加权的 MLE就正态分布来说类似

 and 

对称的:

 and .

这个例子来自Answers.com的Expectation-maximization algorithm，由于还没有深入体验，心里还说不出一些更通俗易懂的东西来，等研究了并且应用了可能就有所理解和消化。另外，liuxqsmile也做了一些理解和翻译。

============

在网上的源码不多，有一个很好的EM_GM.m，是滑铁卢大学的Patrick P. C. Tsui写的，拿来分享一下：

运行的时候可以如下进行初始化：

 % matlab code
 X = zeros(,);
 X(:,:) = normrnd(,,,);
 X(:,:) = normrnd(,,,);
 X(:,:) = normrnd(,,,);
 [W,M,V,L] = EM_GM(X,,[],[],,[])

下面是程序源码：

 %matlab code

 function [W,M,V,L] = EM_GM(X,k,ltol,maxiter,pflag,Init)
 % [W,M,V,L] = EM_GM(X,k,ltol,maxiter,pflag,Init)
 %
 % EM algorithm for k multidimensional Gaussian mixture estimation
 %
 % Inputs:
 %   X(n,d) - input data, n=number of observations, d=dimension of variable
 %   k - maximum number of Gaussian components allowed
 %   ltol - percentage of the log likelihood difference between  iterations ([] for none)
 %   maxiter - maximum number of iteration allowed ([] for none)
 %   pflag -  for plotting GM for 1D or 2D cases only,  otherwise ([] for none)
 %   Init - structure of initial W, M, V: Init.W, Init.M, Init.V ([] for none)
 %
 % Ouputs:
 %   W(,k) - estimated weights of GM
 %   M(d,k) - estimated mean vectors of GM
 %   V(d,d,k) - estimated covariance matrices of GM
 %   L - log likelihood of estimates
 %
 % Written by
 %   Patrick P. C. Tsui,
 %   PAMI research group
 %   Department of Electrical and Computer Engineering
 %   University of Waterloo,
 %   March,
 %

 %%%% Validate inputs %%%%
 if nargin <= ,
  disp('EM_GM must have at least 2 inputs: X,k!/n')
  return
 elseif nargin == ,
  ltol = 0.1; maxiter = ; pflag = ; Init = [];
  err_X = Verify_X(X);
  err_k = Verify_k(k);
  if err_X | err_k, return; end
 elseif nargin == ,
  maxiter = ; pflag = ; Init = [];
  err_X = Verify_X(X);
  err_k = Verify_k(k);
  [ltol,err_ltol] = Verify_ltol(ltol);
  if err_X | err_k | err_ltol, return; end
 elseif nargin == ,
  pflag = ;  Init = [];
  err_X = Verify_X(X);
  err_k = Verify_k(k);
  [ltol,err_ltol] = Verify_ltol(ltol);
  [maxiter,err_maxiter] = Verify_maxiter(maxiter);
  if err_X | err_k | err_ltol | err_maxiter, return; end
 elseif nargin == ,
  Init = [];
  err_X = Verify_X(X);
  err_k = Verify_k(k);
  [ltol,err_ltol] = Verify_ltol(ltol);
  [maxiter,err_maxiter] = Verify_maxiter(maxiter);
  [pflag,err_pflag] = Verify_pflag(pflag);
  if err_X | err_k | err_ltol | err_maxiter | err_pflag, return; end
 elseif nargin == ,
  err_X = Verify_X(X);
  err_k = Verify_k(k);
  [ltol,err_ltol] = Verify_ltol(ltol);
  [maxiter,err_maxiter] = Verify_maxiter(maxiter);
  [pflag,err_pflag] = Verify_pflag(pflag);
  [Init,err_Init]=Verify_Init(Init);
  if err_X | err_k | err_ltol | err_maxiter | err_pflag | err_Init, return; end
 else
  disp('EM_GM must have 2 to 6 inputs!');
  return
 end

 %%%% Initialize W, M, V,L %%%%
 t = cputime;
 if isempty(Init),
  [W,M,V] = Init_EM(X,k); L = ;
 else
  W = Init.W;
  M = Init.M;
  V = Init.V;
 end
 Ln = Likelihood(X,k,W,M,V); % Initialize log likelihood
 Lo = *Ln;

 %%%% EM algorithm %%%%
 niter = ;
 while (abs(*(Ln-Lo)/Lo)>ltol) & (niter<=maxiter),
  E = Expectation(X,k,W,M,V); % E-step
  [W,M,V] = Maximization(X,k,E);  % M-step
  Lo = Ln;
  Ln = Likelihood(X,k,W,M,V);
  niter = niter + ;
 end
 L = Ln;

 %%%% Plot 1D or 2D %%%%
 if pflag==,
  [n,d] = size(X);
  if d>,
  disp('Can only plot 1 or 2 dimensional applications!/n');
  else
  Plot_GM(X,k,W,M,V);
  end
  elapsed_time = sprintf('CPU time used for EM_GM: %5.2fs',cputime-t);
  disp(elapsed_time);
  disp(sprintf('Number of iterations: %d',niter-));
 end
 %%%%%%%%%%%%%%%%%%%%%%
 %%%% End of EM_GM %%%%
 %%%%%%%%%%%%%%%%%%%%%%

 function E = Expectation(X,k,W,M,V)
 [n,d] = size(X);
 a = (*pi)^(0.5*d);
 S = zeros(,k);
 iV = zeros(d,d,k);
 for j=:k,
  if V(:,:,j)==zeros(d,d), V(:,:,j)=ones(d,d)*eps; end
  S(j) = sqrt(det(V(:,:,j)));
  iV(:,:,j) = inv(V(:,:,j));
 end
 E = zeros(n,k);
 for i=:n,
  for j=:k,
  dXM = X(i,:)'-M(:,j);
  pl = exp(-0.5*dXM'*iV(:,:,j)*dXM)/(a*S(j));
  E(i,j) = W(j)*pl;
  end
  E(i,:) = E(i,:)/sum(E(i,:));
 end
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Expectation %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%

 function [W,M,V] = Maximization(X,k,E)
 [n,d] = size(X);
 W = zeros(,k); M = zeros(d,k);
 V = zeros(d,d,k);
 for i=:k,  % Compute weights
  for j=:n,
  W(i) = W(i) + E(j,i);
  M(:,i) = M(:,i) + E(j,i)*X(j,:)';
  end
  M(:,i) = M(:,i)/W(i);
 end
 for i=:k,
  for j=:n,
  dXM = X(j,:)'-M(:,i);
  V(:,:,i) = V(:,:,i) + E(j,i)*dXM*dXM';
  end
  V(:,:,i) = V(:,:,i)/W(i);
 end
 W = W/n;
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Maximization %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%

 function L = Likelihood(X,k,W,M,V)
 % Compute L based on K. V. Mardia, "Multivariate Analysis", Academic Press, , PP. -
 % to enchance computational speed
 [n,d] = size(X);
 U = mean(X)';
 S = cov(X);
 L = ;
 for i=:k,
  iV = inv(V(:,:,i));
  L = L + W(i)*(-0.5*n*log(det(*pi*V(:,:,i))) ...
  -0.5*(n-)*(trace(iV*S)+(U-M(:,i))'*iV*(U-M(:,i))));
 end
 %%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Likelihood %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%

 function err_X = Verify_X(X)
 err_X = ;
 [n,d] = size(X);
 if n<d,
  disp('Input data must be n x d!/n');
  return
 end
 err_X = ;
 %%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Verify_X %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%

 function err_k = Verify_k(k)
 err_k = ;
 if ~isnumeric(k) | ~isreal(k) | k<,
  disp('k must be a real integer >= 1!/n');
  return
 end
 err_k = ;
 %%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Verify_k %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%

 function [ltol,err_ltol] = Verify_ltol(ltol)
 err_ltol = ;
 if isempty(ltol),
  ltol = 0.1;
 elseif ~isreal(ltol) | ltol<=,
  disp('ltol must be a positive real number!');
  return
 end
 err_ltol = ;
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Verify_ltol %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%

 function [maxiter,err_maxiter] = Verify_maxiter(maxiter)
 err_maxiter = ;
 if isempty(maxiter),
  maxiter = ;
 elseif ~isreal(maxiter) | maxiter<=,
  disp('ltol must be a positive real number!');
  return
 end
 err_maxiter = ;
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Verify_maxiter %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

 function [pflag,err_pflag] = Verify_pflag(pflag)
 err_pflag = ;
 if isempty(pflag),
  pflag = ;
 elseif pflag~= & pflag~=,
  disp('Plot flag must be either 0 or 1!/n');
  return
 end
 err_pflag = ;
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Verify_pflag %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%

 function [Init,err_Init] = Verify_Init(Init)
 err_Init = ;
 if isempty(Init),
  % Do nothing;
 elseif isstruct(Init),
  [Wd,Wk] = size(Init.W);
  [Md,Mk] = size(Init.M);
  [Vd1,Vd2,Vk] = size(Init.V);
  if Wk~=Mk | Wk~=Vk | Mk~=Vk,
  disp('k in Init.W(1,k), Init.M(d,k) and Init.V(d,d,k) must equal!/n')
  return
  end
  if Md~=Vd1 | Md~=Vd2 | Vd1~=Vd2,
  disp('d in Init.W(1,k), Init.M(d,k) and Init.V(d,d,k) must equal!/n')
  return
  end
 else
  disp('Init must be a structure: W(1,k), M(d,k), V(d,d,k) or []!');
  return
 end
 err_Init = ;
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Verify_Init %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%

 function [W,M,V] = Init_EM(X,k)
 [n,d] = size(X);
 [Ci,C] = kmeans(X,k,'Start','cluster', ...
  'Maxiter',, ...
  'EmptyAction','drop', ...
  'Display','off'); % Ci(nx1) - cluster indeices; C(k,d) - cluster centroid (i.e. mean)
 while sum(isnan(C))>,
  [Ci,C] = kmeans(X,k,'Start','cluster', ...
  'Maxiter',, ...
  'EmptyAction','drop', ...
  'Display','off');
 end
 M = C';
 Vp = repmat(struct('count',,'X',zeros(n,d)),,k);
 for i=:n, % Separate cluster points
  Vp(Ci(i)).count = Vp(Ci(i)).count + ;
  Vp(Ci(i)).X(Vp(Ci(i)).count,:) = X(i,:);
 end
 V = zeros(d,d,k);
 for i=:k,
  W(i) = Vp(i).count/n;
  V(:,:,i) = cov(Vp(i).X(:Vp(i).count,:));
 end
 %%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Init_EM %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%

 function Plot_GM(X,k,W,M,V)
 [n,d] = size(X);
 if d>,
  disp('Can only plot 1 or 2 dimensional applications!/n');
  return
 end
 S = zeros(d,k);
 R1 = zeros(d,k);
 R2 = zeros(d,k);
 for i=:k,  % Determine plot range as  x standard deviations
  S(:,i) = sqrt(diag(V(:,:,i)));
  R1(:,i) = M(:,i)-*S(:,i);
  R2(:,i) = M(:,i)+*S(:,i);
 end
 Rmin = min(min(R1));
 Rmax = max(max(R2));
 R = [Rmin:0.001*(Rmax-Rmin):Rmax];
 clf, hold on
 if d==,
  Q = zeros(size(R));
  for i=:k,
  P = W(i)*normpdf(R,M(:,i),sqrt(V(:,:,i)));
  Q = Q + P;
  plot(R,P,'r-'); grid on,
  end
  plot(R,Q,'k-');
  xlabel('X');
  ylabel('Probability density');
 else % d==
  plot(X(:,),X(:,),'r.');
  for i=:k,
  Plot_Std_Ellipse(M(:,i),V(:,:,i));
  end
  xlabel('1^{st} dimension');
  ylabel('2^{nd} dimension');
  axis([Rmin Rmax Rmin Rmax])
 end
 title('Gaussian Mixture estimated by EM');
 %%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Plot_GM %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%

 function Plot_Std_Ellipse(M,V)
 [Ev,D] = eig(V);
 d = length(M);
 if V(:,:)==zeros(d,d),
  V(:,:) = ones(d,d)*eps;
 end
 iV = inv(V);
 % Find the larger projection
 P = [,;,];  % X-axis projection operator
 P1 = P * *sqrt(D(,)) * Ev(:,);
 P2 = P * *sqrt(D(,)) * Ev(:,);
 if abs(P1()) >= abs(P2()),
  Plen = P1();
 else
  Plen = P2();
 end
 count = ;
 step = 0.001*Plen;
 Contour1 = zeros(,);
 Contour2 = zeros(,);
 for x = -Plen:step:Plen,
  a = iV(,);
  b = x * (iV(,)+iV(,));
  c = (x^) * iV(,) - ;
  Root1 = (-b + sqrt(b^ - *a*c))/(*a);
  Root2 = (-b - sqrt(b^ - *a*c))/(*a);
  if isreal(Root1),
  Contour1(count,:) = [x,Root1] + M';
  Contour2(count,:) = [x,Root2] + M';
  count = count + ;
  end
 end
 Contour1 = Contour1(:count-,:);
 Contour2 = [Contour1(,:);Contour2(:count-,:);Contour1(count-,:)];
 plot(M(),M(),'k+');
 plot(Contour1(:,),Contour1(:,),'k-');
 plot(Contour2(:,),Contour2(:,),'k-');
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%% End of Plot_Std_Ellipse %%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

from: http://www.zhizhihu.com/html/y2010/2109.html