Loj10153 二叉苹果树

题目描述

有一棵二叉苹果树，如果数字有分叉，一定是分两叉，即没有只有一个儿子的节点。这棵树共 NN 个节点，标号 11 至 NN，树根编号一定为 11。

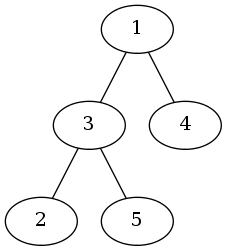
我们用一根树枝两端连接的节点编号描述一根树枝的位置。一棵有四根树枝的苹果树，因为树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。

输入格式

第一行两个数 NN 和 QQ ，NN 表示树的节点数，QQ 表示要保留的树枝数量。

接下来 N-1N−1 行描述树枝信息，每行三个整数，前两个是它连接的节点的编号，第三个数是这根树枝上苹果数量。

输出格式

输出仅一行，表示最多能留住的苹果的数量。

一眼，是树形DP，其中dp[i][j]代表以i为根节点的子树中，保留j个节点能取到的最大数量。

对于每一个节点，枚举左子树的保留节点数，则右子树保留节点数就是总结点数减去左子树。

根据这个进行记忆化搜索。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#define in(a) a=read()
#define REP(i,k,n)  for(int i=k;i<=n;i++)
using namespace std;
inline int read(){
    int x=,f=;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar())
        if(ch=='-')
            f=-;
    for(;isdigit(ch);ch=getchar())
        x=x*+ch-'';
    return x*f;
}
int n,m;
int l[],r[],s[];
int f[][];
inline int dfs(int i,int j){
    if(!j)  return ;
    if(!l[i] && !r[i])  return s[i];
    if(f[i][j])  return f[i][j];
    REP(k,,j-)
        f[i][j]=max(f[i][j],dfs(l[i],k)+dfs(r[i],j-k-)+s[i]);
    return f[i][j];
}
int total,head[],to[],nxt[],val[];
inline void adl(int a,int b,int c){
    total++;
    to[total]=b;
    val[total]=c;
    nxt[total]=head[a];
    head[a]=total;
    return ;
}
inline void get(int u,int fa){
    for(int e=head[u];e;e=nxt[e])
        if(to[e]!=fa){
            if(!l[u])  l[u]=to[e];
            else  r[u]=to[e];
            s[to[e]]=val[e];
            get(to[e],u);
        }
    return ;
}
int main(){
    in(n),in(m);
    int a,b,c;
    REP(i,,n-)  in(a),in(b),in(c),adl(a,b,c),adl(b,a,c);
    get(,);
    cout<<dfs(,m+)<<endl;
    return ;
}