bzoj 4176: Lucas的数论 -- 杜教筛，莫比乌斯反演

4176: Lucas的数论

Time Limit: 30 Sec  Memory Limit: 256 MB

Description

去年的Lucas非常喜欢数论题，但是一年以后的Lucas却不那么喜欢了。

在整理以前的试题时，发现了这样一道题目“求Sigma(f(i)),其中1<=i<=N”，其中 表示i的约数个数。他现在长大了，题目也变难了。

求如下表达式的值：

 

其中 表示ij的约数个数。

他发现答案有点大，只需要输出模1000000007的值。

Input

第一行一个整数n。

Output

一行一个整数ans，表示答案模1000000007的值。

Sample Input

2

Sample Output

8

HINT

对于100%的数据n <= 10^9。

 

Source

emmmm，转载一份题解吧，写的很清晰了 http://blog.csdn.net/clove_unique/article/details/67633389

我们先反演一下，化简成这样

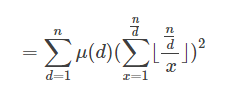
然后就括号内的东西可以O(√n)算出，然后杜教筛出mu值，就可以了

（复杂度不要问我qwq

#include<map>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define mod 1000000007
#define ll long long
#define N 1000555
int mu[N],pri[N],tot;
bool vs[N];
void INIT()
{
    mu[]=;
    for(int i=;i<N;i++)
    {
        if(!vs[i]) pri[++tot]=i,mu[i]=-;
        for(int j=;j<=tot&&pri[j]*i<N;j++)
        {
            vs[pri[j]*i]=;
            if(i%pri[j]==){mu[pri[j]*i]=;break;}
            mu[pri[j]*i]=-mu[i];
        }
        mu[i]+=mu[i-];
    }
}
int n;
ll ans;
ll F(int x)
{
    ll tp=;
    for(int i=,j;i<=x;i=j+)
    {
        j=x/(x/i);
        (tp+=(ll)(x/i)*(j-i+))%=mod;
    }
    return tp*tp%mod;
}
map<int,int>p;
ll sol(int x)
{
    if(x<N) return mu[x];
    if(p[x]) return p[x];
    ll ta=;
    for(int i=,j;i<=x;i=j+)
    {
        j=x/(x/i);
        (ta-=sol(x/i)*(j-i+))%=mod;
    }
    if(ta<) ta+=mod;
    return p[x]=ta;
}
int main()
{
    INIT();
    scanf("%d",&n);
    for(int i=,j;i<=n;i=j+)
    {
        j=n/(n/i);
        (ans+=F(n/i)*(sol(j)-sol(i-)+mod))%=mod;
    }
    printf("%lld\n",ans);
    return ;
}