HDU1693 Eat the Trees（zerojudge a228）

传送门：

https://zerojudge.tw/ShowProblem?problemid=a228

http://acm.hdu.edu.cn/showproblem.php?pid=1693

【题解】

插头dp第一题（难以置信我高中oi没有写过23333）

方程很简单，自己推一推插头的地方的连通性即可

放几张图跑了

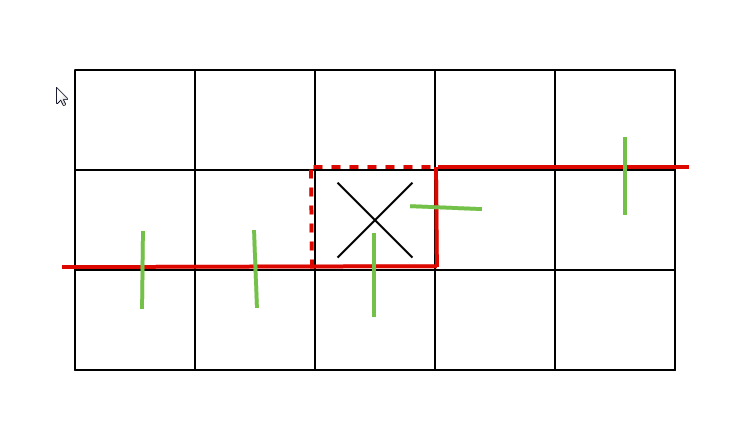
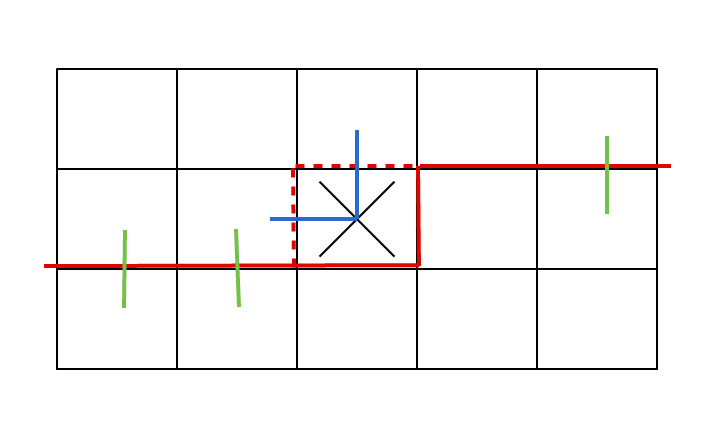
# include <stdio.h>
# include <string.h>
# include <iostream>
# include <algorithm>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;

const int M =  + , MAX_STATUS = ( << ) + ;
const int mod = 1e9 + ;

int n, m, a[M][M], tCase = ;
ll f[M][M][MAX_STATUS];

inline void sol() {
  cin >> n >> m;
  for (int i=; i<=n; ++i)
    for (int j=; j<=m; ++j)
      scanf("%d", &a[i][j]);
  int STATUS_SIZE = ( << m+) - ;
  int STATUS_SIZE_T = ( << m) - ;
  f[][m][] = ;
  for (int i=; i<=n; ++i) {
    for (int sta=; sta<=STATUS_SIZE_T; ++sta) f[i][][sta << ] = f[i-][m][sta];
    for (int j=; j<=m; ++j)
      for (int sta=; sta<=STATUS_SIZE; ++sta) {
        bool cur1 = (sta & ( << j-)), cur2 = (sta & ( << j));
        if(a[i][j] == ) {
          if(cur1 && cur2) f[i][j][sta] = f[i][j-][sta - ( << j-) - ( << j)];
          else if(cur1 ^ cur2) {
            int STA = (sta | ( << j-) | ( << j));
            f[i][j][sta] = f[i][j-][STA - ( << j-)] + f[i][j-][STA - ( << j)];
          } else f[i][j][sta] = f[i][j-][sta | ( << j-) | ( << j)];
        } else {
          if(!cur1 && !cur2) f[i][j][sta] = f[i][j-][sta];
          else f[i][j][sta] = ;
        }
      }
  }
  cout << "Case " << ++tCase << ": There are " << f[n][m][] << " ways to eat the trees.\n";
}

int main() {
  int T;
  cin >> T;
  while(T--) sol();
    return ;
}

# include <stdio.h>
# include <string.h>
# include <iostream>
# include <algorithm>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;

const int M =  + , MAX_STATUS = ( << ) + ;
const int mod = 1e9 + ;

int n, m, a[M][M], tCase = ;
int f[M][M][MAX_STATUS];

inline void sol() {
  cin >> n >> m;
  for (int i=; i<=n; ++i)
    for (int j=; j<=m; ++j)
      scanf("%d", &a[i][j]);
  int STATUS_SIZE = ( << m+) - ;
  int STATUS_SIZE_T = ( << m) - ;
  f[][m][] = ;
  for (int i=; i<=n; ++i) {
    for (int sta=; sta<=STATUS_SIZE_T; ++sta) f[i][][sta << ] = f[i-][m][sta];
    for (int j=; j<=m; ++j)
      for (int sta=; sta<=STATUS_SIZE; ++sta) {
        bool cur1 = (sta & ( << j-)), cur2 = (sta & ( << j));
        if(a[i][j] == ) {
          if(cur1 && cur2) f[i][j][sta] = f[i][j-][sta - ( << j-) - ( << j)];
          else if(cur1 ^ cur2) {
            int STA = (sta | ( << j-) | ( << j));
            f[i][j][sta] = f[i][j-][STA - ( << j-)] + f[i][j-][STA - ( << j)];
            if(f[i][j][sta] >= mod) f[i][j][sta] -= mod;
          } else f[i][j][sta] = f[i][j-][sta | ( << j-) | ( << j)];
        } else {
          if(!cur1 && !cur2) f[i][j][sta] = f[i][j-][sta];
          else f[i][j][sta] = ;
        }
      }
  }
  cout << "Case " << ++tCase << ": " << f[n][m][] << endl;
}

int main() {
  int T;
  cin >> T;
  while(T--) sol();
    return ;
}

上面hdu，下面zerojudge