51nod 1589 移数博弈 | 基数排序(ノಠ益ಠ)ノ彡┻━┻

51nod 1589 移数博弈

题面

给出一个序列a，长度 n <= 10^7, a[i] <= 10^7

求每个长度 >= 2 的区间的最大值*次大值 之和。

题解

主要思路是求每个元素作为次大值做了多少贡献。

对于一个元素 a[i], 设从i向左走能找到的第一个比a[i]大的位置为l[i], 第二个比a[i]大的位置为ll[i], 向右走能找到的第一个比a[i]大的位置为r[i], 第二个为rr[i]。

a[i]作为次大值的时候，区间最大值要么是a[l[i]], 要么是a[r[i]]。

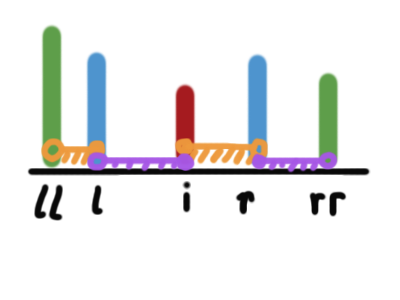
如上图（竖直柱表示不同大小的数，之前未画出的均比a[i]小），若a[l[i]]是最大值，那么区间左、右端点应分别在橙色区间的两部分中；否则应该在紫色区间的两部分中。

对应计算区间数量求贡献即可。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
    char c;
    bool op = 0;
    while(c = getchar(), c < '0' || c > '9')
        if(c == '-') op = 1;
    x = c - '0';
    while(c = getchar(), c >= '0' && c <= '9')
        x = x * 10 + c - '0';
    if(op) x = -x;
}
template <class T>
void write(T x){
    if(x < 0) x = -x, putchar('-');
    if(x >= 10) write(x / 10);
    putchar('0' + x % 10);
}

const int N = 1e7 + 5, P = 1e9 + 7;
int n, A, B, p, a[N], b[N], cnt[N], pre[N], nxt[N];
ll ans;
//b[i]是a中排名第i的元素的位置

int main(){
    read(n), read(a[0]), read(A), read(B), read(p);
    for(int i = 1; i <= n; i++)
        a[i] = ((ll)a[i - 1] * A + B) % p, cnt[a[i]]++;
    a[0] = 0;
    for(int i = 1; i <= 1e7; i++)
        cnt[i] += cnt[i - 1];
    for(int i = n; i; i--)
        b[cnt[a[i]]--] = i;
    for(int i = 0; i <= n + 1; i++)
        pre[i] = i - 1, nxt[i] = i + 1;
    pre[0] = 0, nxt[n + 1] = n + 1;
    for(int i = 1; i <= n; i++){
        ans = (ans + (ll) a[b[i]] * a[pre[b[i]]] % P
               * (pre[b[i]] - pre[pre[b[i]]]) % P
               * (nxt[b[i]] - b[i]) % P) % P;
        ans = (ans + (ll) a[b[i]] * a[nxt[b[i]]] % P
               * (nxt[nxt[b[i]]] - nxt[b[i]]) % P
               * (b[i] - pre[b[i]]) % P) % P;
        pre[nxt[b[i]]] = pre[b[i]];
        nxt[pre[b[i]]] = nxt[b[i]];
    }
    write(ans), putchar('\n');
    return 0;
}