洛谷 P1073 最优贸易

---

---

题目描述

CC C 国有 n n n 个大城市和 m mm 条道路，每条道路连接这 nnn 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 mmm 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 11 1 条。

CC C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 CCC 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 CCC 国 n 个城市的标号从 1 n1~ n1 n ，阿龙决定从 11 1 号城市出发，并最终在 nnn 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 nnn 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 CCC 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 CC C 国有 555 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

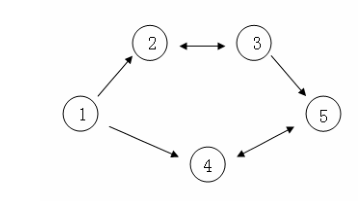
假设 1 n1~n1 n 号城市的水晶球价格分别为 4,3,5,6,14,3,5,6,14,3,5,6,1 。

阿龙可以选择如下一条线路： 111 -> 222 -> 333 -> 555 ，并在 22 2 号城市以 3 33 的价格买入水晶球，在 333 号城市以 5 5 5 的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路 1 11 -> 444 -> 555 -> 444 -> 555 ，并在第 11 1 次到达 5 55 号城市时以 11 1 的价格买入水晶球，在第 222 次到达 4 44 号城市时以 6 66 的价格卖出水晶球，赚取的旅费数为 5 55 。

现在给出 nn n 个城市的水晶球价格， mmm 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入输出格式

输入格式：

第一行包含 222 个正整数 n n n 和 mmm ，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 mmm 行，每行有 3 3 3 个正整数 x,y,zx,y,zx,y,z ，每两个整数之间用一个空格隔开。如果 z=1z=1z=1 ，表示这条道路是城市 x x x 到城市 y y y 之间的单向道路；如果 z=2 z=2z=2 ，表示这条道路为城市 xx x 和城市 yy y 之间的双向道路。

输出格式：

一 个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 000 。

输入输出样例

输入样例#1：

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2 

输出样例#1：

5

说明

【数据范围】

输入数据保证 111 号城市可以到达 n n n 号城市。

对于 10%的数据， 1≤n≤61≤n≤61≤n≤6 。

对于 30%的数据， 1≤n≤1001≤n≤1001≤n≤100 。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据， 1≤n≤1000001≤n≤1000001≤n≤100000 ， 1≤m≤5000001≤m≤5000001≤m≤500000 ， 1≤x1≤x1≤x ， y≤ny≤ny≤n ， 1≤z≤21≤z≤21≤z≤2 ， 1≤1≤1≤ 各城市

水晶球价格 ≤100≤100≤100 。

NOIP 2009 提高组 第三题

---

缩点做法：

1.用tarjan缩点

2.用dfs判断每一个点是否在1到n 的有效路径上（剪枝，没加T了一次

3.将在路径上的点进行拓扑排序，同时求到每个点之前的最小价格与这个点的价格相减后取max为答案

---

#include<iostream>
#include<stdio.h>
#include<cstring>
#include<queue>

using namespace std;
priority_queue <pair<int,int> >q;
int cnt,u,i,m,n,j,a[200001],ver[200001],nex[200001],head[200001],g,h,k,ru[200001],chu[200001];
int dfn[200001],low[200001],sta[200001],top,f[200001],maxx,fr[200001],minn[200100],z[200001];
int d[100001];
bool vis[200001],bl[100001];
void add(int x,int y)
{
	cnt+=1;
	ver[cnt]=y;
	nex[cnt]=head[x];
	head[x]=cnt;
	fr[cnt]=x;
}

void dfs(int x)
{
	cnt+=1;
	dfn[x]=low[x]=cnt; top+=1; sta[top]=x; vis[x]=1;
	for(int i=head[x];i;i=nex[i])
	{
		int t=ver[i];
		if(!dfn[t])
		{
			dfs(t);
			low[x]=min(low[x],low[t]);
		}
		else if(vis[t]) low[x]=min(low[x],dfn[t]);
	}
	if(dfn[x]==low[x])
	{
		u+=1;
		do
		{
			if(ru[u]>a[sta[top]]) ru[u]=a[sta[top]];
			if(chu[u]<a[sta[top]]) chu[u]=a[sta[top]];
			f[sta[top]]=u;
			vis[sta[top]]=0;
		} while(sta[top--]!=x);
	}
}

bool dfss(int x)
{
	vis[x]=1;
	if(x==f[n])
	{
		bl[x]=1;
		return 1;
	}
	for(int i=head[x];i;i=nex[i])
	{
		int t=ver[i];
		if(!vis[t]) bl[x]=(dfss(t) || bl[x]);
		bl[x]=(bl[x] || bl[t]);
	}
	return bl[x];
}

void search(int x,int y)
{
	maxx=max(maxx,chu[x]-min(ru[x],y));
	for(int i=head[x];i;i=nex[i])
	{
		d[ver[i]]-=1;
		if(!d[ver[i]]) search(ver[i],min(y,ru[x]));
	}

}

int main()
{
	memset(ru,0x3f,sizeof(ru));
	memset(minn,0x3f,sizeof(minn));
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++) scanf("%d",&a[i]);
	for(i=1;i<=m;i++)
	{
		scanf("%d%d%d",&g,&h,&k);
		add(g,h);
		if(k==2) add(h,g);
	}
	m=cnt;
	cnt=0;
	for(i=1;i<=n;i++) if(!dfn[i]) dfs(i);

	cnt=0;
	memset(head,0,sizeof(head));
	for(i=1;i<=m;i++)
		if(f[fr[i]]!=f[ver[i]])
			add(f[fr[i]],f[ver[i]]);
	dfss(f[1]);
	for(i=1;i<=cnt;i++) if(bl[fr[i]] && bl[ver[i]]) d[ver[i]]+=1;
	search(f[1],0x7fffffff);
	printf("%d",maxx);
}