Python解决八皇后问题的代码【解读】

八皇后问题 来自于西方象棋（现在叫 国际象棋，英文chess），详情可见百度百科。

在西方象棋中，有一种叫做皇后的棋子，在棋盘上，如果双方的皇后在同一行、同一列或同一斜线上，就会互相攻击。

八皇后问题：

在8行8列的棋盘上摆放8个皇后，使之不能互相攻击——任意两个不在同一行、同一列或同一斜线上。

Level 1：找到一种摆放的方法

Level 2：找到总共有多少种方法

----------

下面展示在《Python基础教程》（第二版·修订版）中看到的解法，本文的目的是对其进行解读，加深自己的理解（今天花了一个多钟想明白）。

应用到的重要技术：生成器、递归算法

解决方法：

Step 1-定义冲突函数

在当前行的8个位置摆放棋子时，检查是否与已摆放的棋子是否冲突。

def conflict(state, nextX):                            #state为已摆放的棋子的位置的元组，比如（1,3,0）
    nextY = len(state)                                 #获取当前行号
    for i in range(nextY):                             #检查每一个已摆放的棋子和当前行要摆放的棋子的位置（nextX, nextY）是否冲突
        if abs(state[i] - nextX) in (0, nextY - i):    #关键！若是两个棋子 行差值 的绝对值 出现在元组 （0，行差值）中，则冲突发生，返回True
            return True
    return False                                       #无冲突，可行的摆放位置

Step 2-递归实现寻找摆放方案

八皇后问题，是否可以拆解为七皇后问题，再拆解为六皇后问题，再……一皇后问题？可以。不过，一皇后、二皇后、三皇后问题都是没有解决方案的。

在摆放最后一个棋子时，前面的棋子已经没有冲突了，那么，最后一步，依次检查在最后一行的每个位置摆放棋子是否和已摆放的棋子是否冲突，如果

不冲突，那么，一种解决方案就有了——递归的终结（书中叫做 基本情况）。

def queens(num=8, state=()):                               #num为棋盘的行数，state为已摆放的棋子的列数汇总，类型为 元组
    if len(state) == num - 1:                              #检查是否最后一行，如果是最后一行，则执行终极操作，不再递归
        for pos in range(num):                             #pos从 0 到 棋盘行数 - 1
            if not conflict(state, pos):                   #检查是否冲突yield (pos,)                               #没有冲突，返回列数的元组
    else:                                                  #不是最后一行
        for pos in range(num):                             #检查当前行每一个列的位置
            if not conflict(state, pos):                   #检查是否有冲突for result in queens(num, state + (pos,)): #递归调用queens，不过找到了更多的一行的摆放位置，所以，加上（pos,）
                                                           #如果是最后一行，返回一个数字的元组，比如，（2）
                                                           #此时，如果pos为0，那么，倒数第二行返回的为两个数字的元组，比如，（0, 2）
                                                           #调用每返回一层，返回的元组的长度就加1，直到最后用户在外部调用queens的位置
                                                           #返回所有行的皇后位置的 元组，其长度为行数
                    yield (pos,) + result                  #这里和想象的有些不同，下面是在Python 2.7.14上运行代码发生的错误
                                                           #程序执行后没问题，可是~~看来还没想明白！（下面有进一步分析）

queens(...)返回的是一个迭代器（生成器 更准确！生成器就是一种迭代器！），因此，下面代码中的result是一个元组，而不是一个数值：

for result in queens(num, state + (pos,))

这样，(pos,) + result就解释的通了！啊哈，明白了！

可以在yield语句上添加打印语句，可以更好地帮助分析。上面想不通的原因在于，将queens(...)返回的内容的类型搞错了，也是不了解

生成器的原理所致，现在理解更深刻啦。

代码改进：

在上面第二份代码中，两个分支中的红色部分是完全相同的，因此，可以对代码进行简化，下面是简化结果。

def queens2(num=8, state=()):
    for pos in range(num):              #重复部分
        if not conflict(state, pos):    #重复部分
            if len(state) == num - 1:   #分支1
                yield (pos,)
            else:                       #分支2
                for result in queens(num, state + (pos,)):
                    yield (pos,) + result

执行结果：

----------

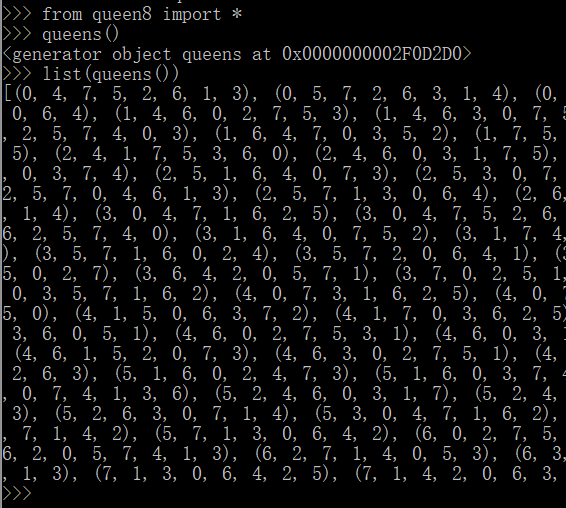
在2.7.14中执行下面的代码发生错误了：试验上面搞不明白的问题