ispoweroftwo 判断2的次幂

首先结果是：

public bool IsPowerOfTwo(int n) {
　　if(n<1) return false;//2的次幂一定大于0
　　return ((n & (n -1)) == 0);
}

分析：2的次幂在计算机中可以用左移(<<)来运算，了解n&(n-1)的作用如下：

n&(n-1)作用：将n的二进制表示中的最低位为1的改为0，先看一个简单的例子：
n = 10100(二进制），则(n-1) = 10011 ==》n&(n-1) = 10000
可以看到原本最低位为1的那位变为0。
弄明白了n&(n-1)的作用，那它有哪些应用？
1. 求某一个数的二进制表示中1的个数
while (n >0 ) {
      count ++;
      n &= (n-1);
}

2. 判断一个数是否是2的方幂
n > 0 && ((n & (n - 1)) == 0 )

3. 计算N!的质因数2的个数。
容易得出N!质因数2的个数 = [N / 2] + [N / 4] + [N / 8] + ....
下面通过一个简单的例子来推导一下过程：N = 10101(二进制表示）
现在我们跟踪最高位的1，不考虑其他位假定为0，
则在
[N / 2]    01000
[N / 4]    00100
[N / 8]    00010
[N / 8]    00001
则所有相加等于01111 = 10000 - 1
由此推及其他位可得：(10101)!的质因数2的个数为10000 - 1 + 00100 - 1 + 00001 - 1 = 10101 - 3(二进制表示中1的个数)

推及一般N!的质因数2的个数为N - （N二进制表示中1的个数）

目前看到只有这些应用，但只要理解了n&(n-1)的原理及作用，在碰到相关问题时也会比较容易解决。

原文：http://6460646.blog.163.com/blog/static/27779875201132893614412/

int n = 16;//一定是大于0的

以下是在C#中 整数的各进制的转化
var x = 2;
Console.WriteLine("n的"+x+"进制为："+Convert.ToString(n,x)+";n-1的2进制:"+Convert.ToString(n-1,x));
x = 8;
Console.WriteLine("n的" + x + "进制为：" + Convert.ToString(n, x) + ";n-1的2进制:" + Convert.ToString(n - 1, x));
x = 10;
Console.WriteLine("n的" + x + "进制为：" + Convert.ToString(n, x) + ";n-1的2进制:" + Convert.ToString(n - 1, x));
x = 16;
Console.WriteLine("n的" + x + "进制为：" + Convert.ToString(n, x) + ";n-1的2进制:" + Convert.ToString(n - 1, x));

var b = n&(n-1);

Console.WriteLine(b);

ps:& 运算符如果不清楚可以和我私聊或者留言

二进制与十进制的相互转换的手动演算如下:

转成二进制主要有以下几种：正整数转二进制，负整数转二进制，小数转二进制；

1、  正整数转成二进制。要点一定一定要记住哈：除二取余，然后倒序排列，高位补零。

2.42除以2得到的余数分别为010101，然后咱们倒着排一下，42所对应二进制就是101010.如图2所示更直观的表达。

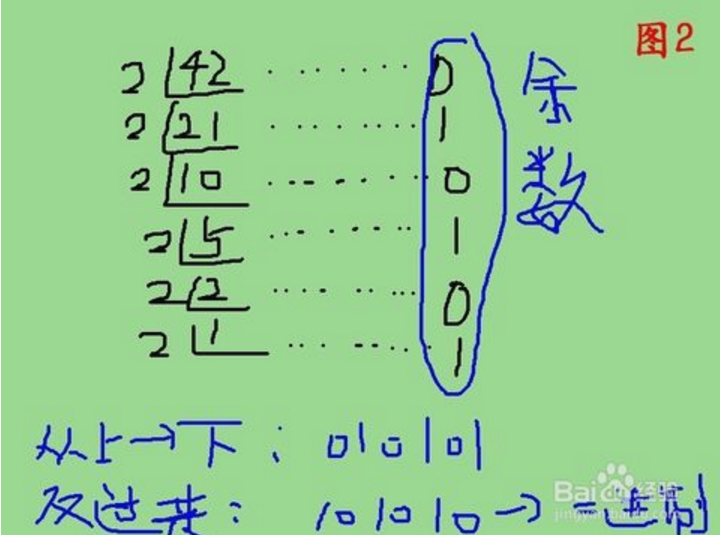
3.计算机内部表示数的字节单位是定长的，如8位，16位，或32位。所以，位数不够时，高位补零，所说，如图3所示，42转换成二进制以后就是。00101010，也即规范的写法为（42）10=（00101010）2.赶紧记住吧。

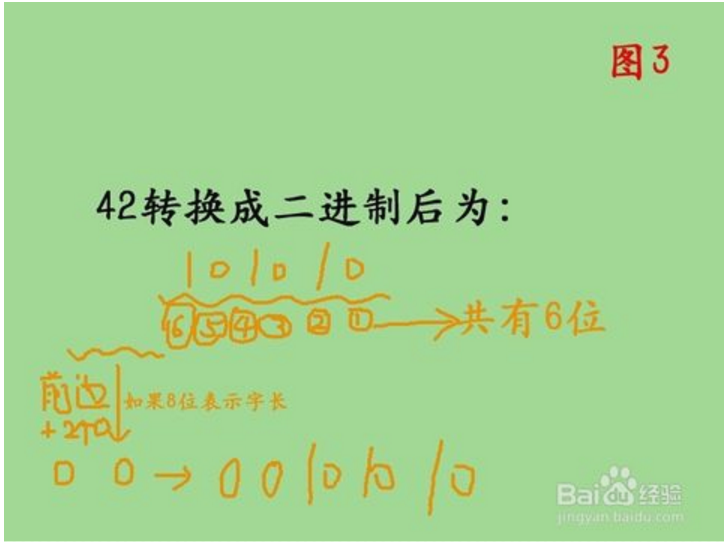
4.2、  负整数转换成二进制

方法：先是将对应的正整数转换成二进制后，对二进制取反，然后对结果再加一。还以42为例，负整数就是-42，如图4所示为方法解释。最后即为：（-42）10=（11010110）2.

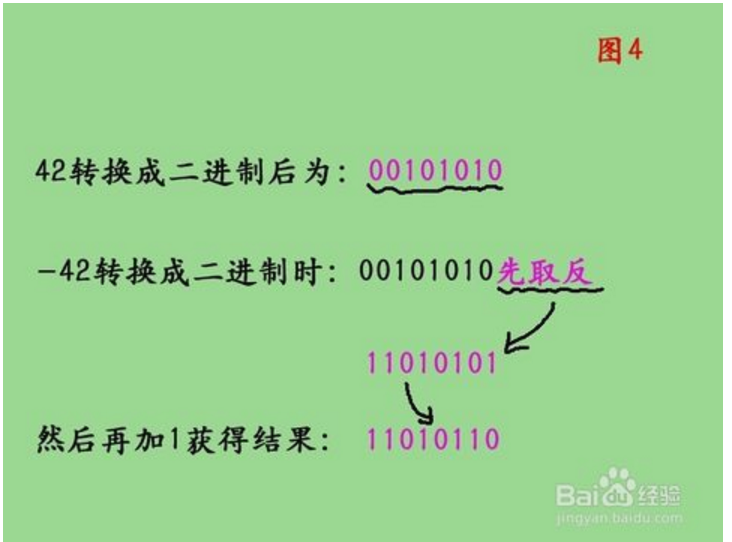
5.小数转换为二进制的方法：对小数点以后的数乘以2，有一个结果吧，取结果的整数部分（不是1就是0喽），然后再用小数部分再乘以2，再取结果的整数部分……以此类推，直到小数部分为0或者位数已经够了就OK了。然后把取的整数部分按先后次序排列就OK了，就构成了二进制小数部分的序列，举个例子吧，比如0.125，如图5所示。

6.如果小数的整数部分有大于0的整数时该如何转换呢？如以上整数转换成二进制，小数转换成二进制，然后加在一起就OK了，如图6所示。

7.

整数二进制转换为十进制：首先将二进制数补齐位数，首位如果是0就代表是正整数，如果首位是1则代表是负整数。

先看首位是0的正整数，补齐位数以后，将二进制中的位数分别将下边对应的值相乘，然后相加得到的就为十进制，比如1010转换为十进制，方法如图7所示。

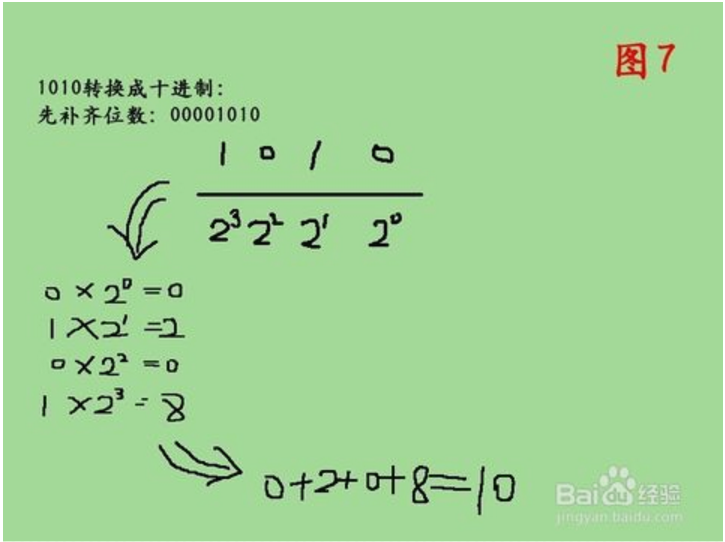
8.若二进制补足位数后首位为1时，就需要先取反再换算：例如，11101011，首位为1，那么就先取反吧：-00010100，然后算一下10100对应的十进制为20，所以对应的十进制为-20，方法如图8所示。

9.将有小数的二进制转换为十进制时：例如0.1101转换为十进制的方法：将二进制中的四位数分别于下边（如图9所示）对应的值相乘后相加得到的值即为换算后的十进制。