二叉树(前序，中序，后序，层序)遍历递归与循环的python实现

二叉树的遍历是在面试使比较常见的项目了。对于二叉树的前中后层序遍历，每种遍历都可以递归和循环两种实现方法，且每种遍历的递归实现都比循环实现要简洁。下面做一个小结。

一、中序遍历

前中后序三种遍历方法对于左右结点的遍历顺序都是一样的（先左后右），唯一不同的就是根节点的出现位置。对于中序遍历来说，根结点的遍历位置在中间。

所以中序遍历的顺序：左中右

1.1 递归实现

每次递归，只需要判断结点是不是None，否则按照左中右的顺序打印出结点value值。

class Solution:
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)

1.2 循环实现

循环比递归要复杂得多，因为你得在一个函数中遍历到所有结点。但是有句话很重要：

对于树的遍历，循环操作基本上要用到栈(stack)这个结构

对于中序遍历的循环实现，每次将当前结点(curr)的左子结点push到栈中，直到当前结点(curr)为None。这时，pop出栈顶的第一个元素，设其为当前结点，并输出该结点的value值，且开始遍历该结点的右子树。

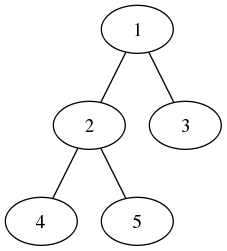
例如，对于上图的一个二叉树，其循环遍历过程如下表：

No.	输出列表sol	栈stack	当前结点curr
1	[]	[]	1
2	[]	[1]	2
3	[]	[1,2]	4
4	[]	[1,2,4]	None
5	[4]	[1,2]	4 -> None(4的右结点)
6	[4,2]	[1]	2 -> 5
7	[4,2]	[1,5]	None(5的左结点)
8	[4,2,5]	[1]	5 -> None(5的右结点)
9	[4,2,5,1]	[]	3
10	[4,2,5,1]	[3]	None
11	[4,2,5,1,3]	[]	None

可见，规律为：当前结点curr不为None时，每一次循环将当前结点curr入栈；当前结点curr为None时，则出栈一个结点，且打印出栈结点的value值。整个循环在stack和curr皆为None的时候结束。

class Solution:
    def inorderTraversal(self, root):
        stack = []
        sol = []
        curr = root
        while stack or curr:
            if curr:
                stack.append(curr)
                curr = curr.left
            else:
                curr = stack.pop()
                sol.append(curr.val)
                curr = curr.right
        return sol

二、前序遍历和后序遍历

按照上面的说法，前序遍历指根结点在最前面输出，所以前序遍历的顺序是：中左右

后序遍历指根结点在最后面输出，所以后序遍历的顺序是：左右中

2.1 递归实现

递归实现与中序遍历几乎完全一样，改变一下打印的顺序即可：

class Solution:
    def preorderTraversal(self, root):  ##前序遍历
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        return  [root.val] + self.inorderTraversal(root.left) + self.inorderTraversal(root.right)

    def postorderTraversal(self, root):  ##后序遍历
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        return  self.inorderTraversal(root.left) + self.inorderTraversal(root.right) + [root.val]

改动的地方只有return时函数的打印顺序。

2.2 循环实现

为什么把前序遍历和后序遍历放在一起呢？Leetcode上前序遍历是medium难度，后序遍历可是hard难度呢！

实际上，后序遍历不就是前序遍历的“反过程”嘛！

先看前序遍历。我们仍然使用栈stack，由于前序遍历的顺序是中左右，所以我们每次先打印当前结点curr，并将右子结点push到栈中，然后将左子结点设为当前结点。入栈和出栈条件（当前结点curr不为None时，每一次循环将当前结点curr入栈；当前结点curr为None时，则出栈一个结点）以及循环结束条件（整个循环在stack和curr皆为None的时候结束）与中序遍历一模一样。

再看后序遍历。由于后序遍历的顺序是左右中，我们把它反过来，则遍历顺序变成中左右，是不是跟前序遍历只有左右结点的差异了呢？然而左右的差异仅仅就是.left和.right的差异，在代码上只有机械的差别。

我们来看代码：

class Solution:
    def preorderTraversal(self, root):  ## 前序遍历
        stack = []
        sol = []
        curr = root
        while stack or curr:
            if curr:
                sol.append(curr.val)
                stack.append(curr.right)
                curr = curr.left
            else:
                curr = stack.pop()
        return sol

    def postorderTraversal(self, root): ## 后序遍历
        stack = []
        sol = []
        curr = root
        while stack or curr:
            if curr:
                sol.append(curr.val)
                stack.append(curr.left)
                curr = curr.right
            else:
                curr = stack.pop()
        return sol[::-1]

代码的主体部分基本就是.right和.left交换了顺序，且后序遍历在最后输出的时候进行了反向（因为要从中右左变为左右中）

三、层序遍历

层序遍历也可以叫做宽度优先遍历：先访问树的第一层结点，再访问树的第二层结点...然后一直访问到最下面一层结点。在同一层结点中，以从左到右的顺序依次访问。

3.1 递归实现

递归函数需要有一个参数level，该参数表示当前结点的层数。遍历的结果返回到一个二维列表sol=[[]]中，sol中的每一个子列表保存了对应index层的从左到右的所有结点value值。

class Solution:
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        def helper(node, level):
            if not node:
                return
            else:
                sol[level-1].append(node.val)
                if len(sol) == level:  # 遍历到新层时，只有最左边的结点使得等式成立
                    sol.append([])
                helper(node.left, level+1)
                helper(node.right, level+1)
        sol = [[]]
        helper(root, 1)
        return sol[:-1]

PS：

Q：如果仍然按层遍历，但是每层从右往左遍历怎么办呢？

A：将上面的代码left和right互换即可

Q：如果仍然按层遍历，但是我要第一层从左往右，第二层从右往左，第三从左往右...这种zigzag遍历方式如何实现？

A：将sol[level-1].append(node.val)进行一个层数奇偶的判断，一个用append()，一个用insert(0,)

    if level%2==1:
        sol[level-1].append(node.val)
    else:
        sol[level-1].insert(0, node.val)

3.2 循环实现

这里的循环实现不能用栈了，得用队列queue。因为每一层都需要从左往右打印，而每打印一个结点都会在队列中依次添加其左右两个子结点，每一层的顺序都是一样的，故必须采用先进先出的数据结构。

以下代码的打印结果为一个一维列表，没有采用二维列表的形式。

class Solution:
    def levelOrder(self, root):
        if not root:
            return []
        sol = []
        curr = root
        queue = [curr]
        while queue:
            curr = queue.pop(0)
            sol.append(curr.val)
            if curr.left:
                queue.append(curr.left)
            if curr.right:
                queue.append(curr.right)
        return sol

其实，如果需要打印成zigzag形式（相邻层打印顺序相反），则可以采用栈stack数据结构，正好符合先进后出的形式。不过在代码上还要进行其他改动。