关于利用GPG加解密的实验

GnuPG（GNU Privacy Guard，简称：GPG）为一款免费开源的使用非对称密钥加密（asymmetric cryptography）之软件，最初由Werner Koch开发，该软件使用非对称密钥（亦称公开密钥加密）提高加密速度，使用公钥便于交换。 GnuPG是自由软件基金会的GNU计划的一部份，与2000年开始接受德国政府资助。以GNU通用公共许可证第三版授权。

本次实验是用自己的笔记本做的。

小组成员：20155309 南皓芯 20155220 吴思其

加解密

加密过程需要双方均安装GnuPG，大致过程为A在本地生成公钥和私钥，将公钥上传到公钥服务器或者直接发送给B，B接受到公钥后对文件进行加密（加密后B无法解密）并将加密文件发送给A，A使用私钥解密，从而避免直接传送密码。

首先我们要在官网上下载GPG，在官网中找到下载一项，并且鼠标下移，在windows中找到gpg4win并且下载。

下载并安装的时候，按照系统提示的命令就好，但是注意到这个程序不要存在c盘中，所以我选择存放到了d盘。最后finish安装即可，最好将其存放在桌面上，打开之后会出现这样的界面。

密钥对生成

首先在运行界面，点击文件，并且选择new key pair 然后出现如下的界面。

然后选择第一项。然后填好自己的姓名，邮箱以及备注。

之后，进行更详尽的配置，选取rsa，默认为2048字节，为了安全起见，设置好有效期。

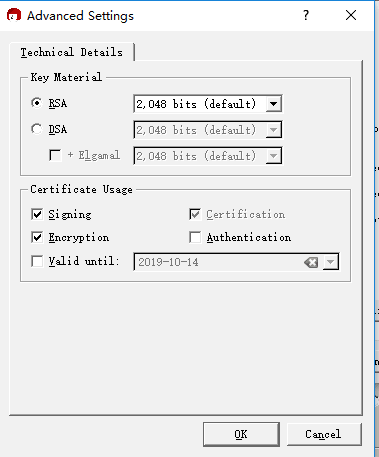
显示出所有参数之后，点击create key继续。之后输入密码。

再次输入密码之后选择ok

密钥对创建完毕后，点击第一个选项进行备份。

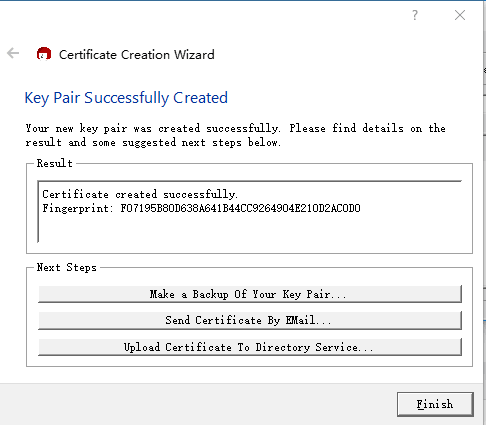
然后确定保存的位置，之后会有信息确保成功导出。

回到主界面可以看到已经生成的密钥对。

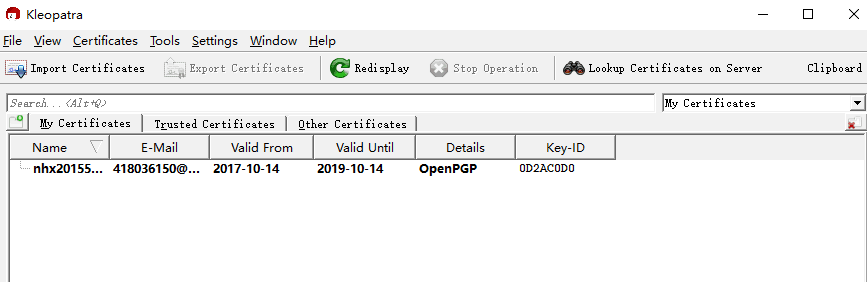
选中密钥对，并且点击鼠标右键，选择export certificate
将密钥对保存至主机文件（asc文件）

系统会提示你已经成功。

用记事本打开这个文件，该文件就是公钥。

我们也可以将密钥上传到公共或私有服务器上，点击鼠标右键，并且选择 export certificate to server

点击continue继续之后，即可发现已经成功。

加密文件

告知对方您公钥的名称及存储公钥服务器，对方打开Kleopatra，点击“Lookup Certificates on Server”。

在主界面依次点击“Settings-->Configure Kleopatra”。

在下图中点击“New”

默认将增加“keys.gnupg.net”服务器，点击“OK”返回主界面。

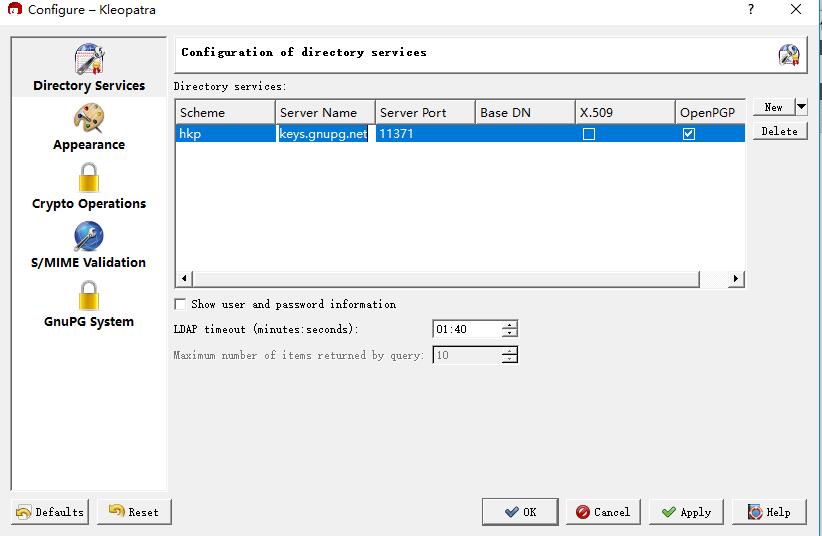
重新点击“Lookup Certificates on Server”,输入公钥名称（nhx20155309）并点击“Search”。

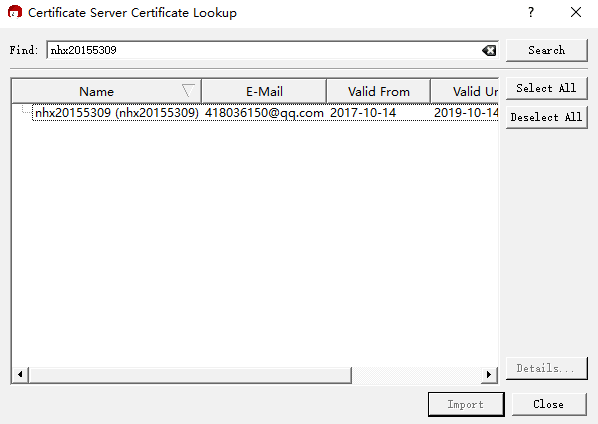
提示已经导入成功

在主界面选择“File”并点击“Sign/Encrypt Files...”（亦可直接拖动需要加密之文件到“My Certificates”栏）。
选取你所要加密的文件（在这里也就是秘密文件）

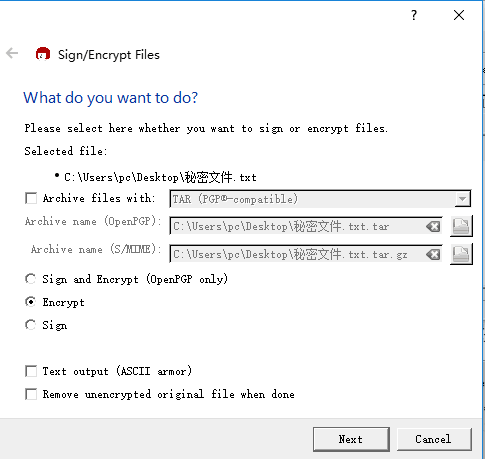
如需加密完毕后直接删除原文件则选择“Remove unencrypted original file when done”,点击“Next>”继续。

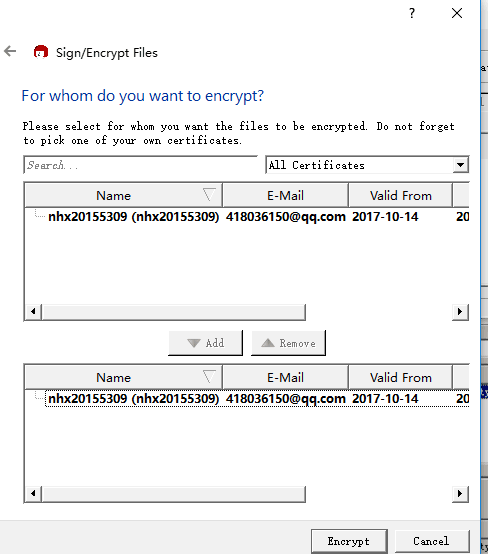
.选择已生成之密钥并点击“Add”按钮后将密钥添加，然后点击“Encrypt”。

加密完毕，提示原文件已被删除。

在原目录里可发现原文件已被删除，新增一个文件名为“原文件名.gpg”的文件，对方将此文件发送给我们即可。

解密文件

收到对方发送的加密文件后，在加密文件（本例中为jiaoxue.db.gpg）点击鼠标右键，选择“Decrypt and verify”。亦可在Kleopatra主界面依次点击“File-->Decrypt/Verify Files...”，找到对方发送的加密文件打开。

直接选取decrypt即可

在加密文件同路径下可看到解密文件，在桌面查看即可。

实验中遇到的问题

在我们下载pgp软件的时候，注意不要下载最新版3.0.0的软件，要下载2.2.2的老版软件，在下载新版软件的时候，在输入rsa的comment的时候，新版的没有这一选项，导致rsa的加解密不能够正确进行。

思考题

根据pgp的加密原理，说明为什么pgp要比RSA加密速度要快得多？

PGP不是加密方法，是一个软件，使用过程中会涉及到很多加密方法，如DES，3DES，RSA，AES等等。
RSA是公钥加密，计算过程涉及到很大的幂指数运算，所以非常慢，一般不用于直接加密明文，通常用于交换密钥。

学习与感悟

首先，通过自行下载pgp以及亲手一步一步进行加解密，自己完全的理解了pgp加解密的原理。在亲手操作的过程中，自己遇到了很多的问题，但是都通过网络与书籍自行解决了。让我了解了做事情不要慌张，只要沉着冷静的思考问题，最后一定会得到自己想要的结果。

PGP加密系统是采用公开密钥加密与传统密钥加密相结合的一种加密技术。它使用一对数学上相关的钥匙，其中一个（公钥）用来加密信息，另一个（私钥）用来解密信息。PGP采用的传统加密技术部分所使用的密钥称为“会话密钥”（sek）。每次使用时，PGP都随机产生一个128位的IDEA会话密钥，用来加密报文。公开密钥加密技术中的公钥和私钥则用来加密会话密钥，并通过它间接地保护报文内容。（参考百度文库）