Find the median（线段树+离散化）（2019牛客暑期多校训练营（第七场））

题目出处：Find the median

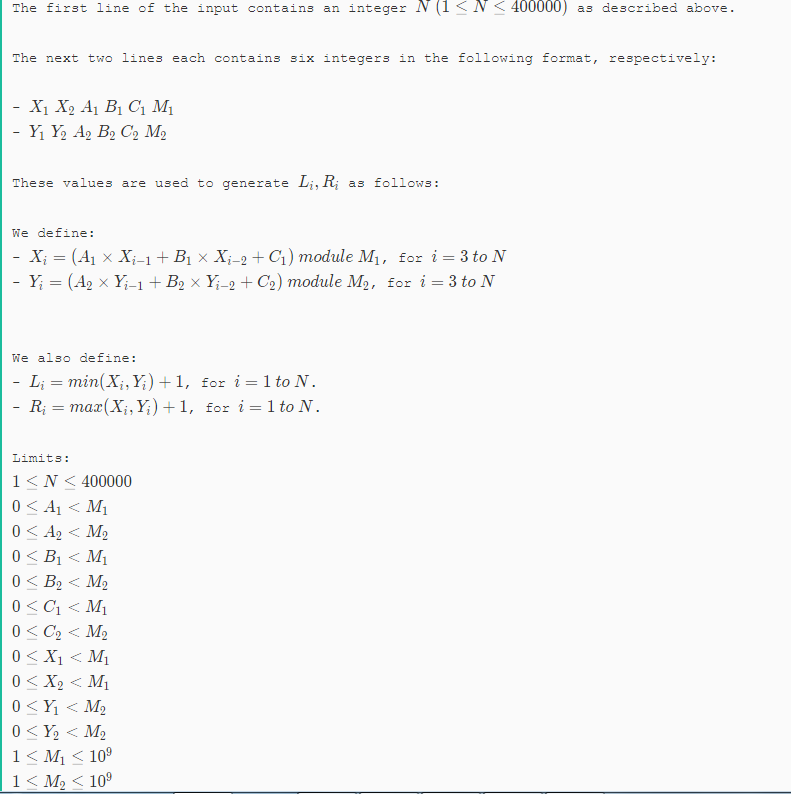
示例：

输入：

5
3 1 4 1 5 9
2 7 1 8 2 9

输出：3 4 5 4 5

说明：L = [3, 2 ,4, 1, 7]，R = [4, 8, 8, 3, 9]

题意：每次插入[l[i],r[i]][l[i],r[i]],询问中位数

题解：线段树模版题+离散化（不懂或忘了这些的先补充下知识）。线段树的区间操作。但是由于范围太大，需要离散化，所以就出现了连续性的问题。所以只能用线段树维护 左闭右开 即：[w[l],w[r])。

code:

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int maxx=8e6+;
LL summ[maxx],w[maxx],lz[maxx];
void pushdown(int l,int r,int root)
{
    if(lz[root]){
        int mid=(l+r)>>;
        summ[root<<]+=(w[mid]-w[l])*lz[root];
        summ[root<<|]+=(w[r]-w[mid])*lz[root];
        lz[root<<]+=lz[root],lz[root<<|]+=lz[root];
        lz[root]=;
    }
}
void update(int l,int r,int root,int L,int R)
{
    if(L<=l&&r-<=R){//更新区间[w[l],w[r]]
        lz[root]++;//将一大段加入每个点加入的数储存，未用的不下放
        summ[root]+=w[r]-w[l];
        return ;
    }
    pushdown(l,r,root);//下放lz标记储存的数
    int mid=(l+r)>>;
    if(L<mid)update(l,mid,root<<,L,R);
    if(R>=mid)update(mid,r,root<<|,L,R);
    summ[root]=summ[root<<]+summ[root<<|];
}
LL query(int l,int r,int root,LL k)
{
    if(l+==r){//当l+1=r时，表示当前最小的一段区间，该区间的数的个数一定相等
        LL lo=summ[root]/(w[r]-w[l]);
        return w[l]+(k-)/lo;
    }
    pushdown(l,r,root);//下发lz标记储存的数
    int mid=(l+r)>>;
    if(summ[root<<]>=k)return query(l,mid,root<<,k);
    else return query(mid,r,root<<|,k-summ[root<<]);
}
LL n,tot=,A1,A2,B1,B2,C1,C2,M1,M2;
LL x[maxx],y[maxx],_l[maxx],_r[maxx];
int main()
{
    scanf("%lld",&n);
    scanf("%lld%lld%lld%lld%lld%lld",&x[],&x[],&A1,&B1,&C1,&M1);
    scanf("%lld%lld%lld%lld%lld%lld",&y[],&y[],&A2,&B2,&C2,&M2);
    for(int i=;i<=n;i++)//按题意算出xi、yi的值
        x[i]=(A1*x[i-]+B1*x[i-]+C1)%M1,y[i]=(A2*y[i-]+B2*y[i-]+C2)%M2;
    for(int i=;i<=n;i++){//按题意处理左右区域和储存所有点以便后面离散化
        _l[i]=min(x[i],y[i])+,_r[i]=max(x[i],y[i])+;//为了得到一个较好的操作区间
        w[tot++]=_l[i],w[tot++]=_r[i];
    }
    sort(w+,w+tot);//排序
    tot=unique(w+,w+tot)-w;//离散化去除重复点
    LL sum=;//统计第几次加入点后点的总数
    for(int i=;i<=n;i++){
        int l=lower_bound(w+,w+tot,_l[i])-w;//
        int r=lower_bound(w+,w+tot,_r[i])-w;
        update(,tot,,l,r-);//在线段树中加入一段新的数据
        sum+=w[r]-w[l];
        printf("%lld\n",query(,tot,,(sum+)/));//查询第i段数据加入后的中位数
    }
    return ;
}