【433】COMP9024 复习
目录:
- 01. Week01 - Lec02 - Revision and setting the scene
- 02. Week02 - Lec01 - Data structures - memory allocation
- 03. Week02 - Lec02 - Input - Output
- 04. Week03 - Lec01 - ADTs
- 05. Week03 - Lec02 - Dynamic memory allocation
- 06. Week04 - Lec01 - LinkedLists
- 07. Week06 - Lec01 - Heaps
- 08. Week06 - Lec02 - Priority Queues and Heap Sort
- 09. Week07 - Lec01 - Graphs
- 10. Week07 - Lec02 - Graph search
- 11. Week08 - Lec02 - Applications of Graph Search
- 12. Week09 - Lec01 - Weighted Graph Algorithms
- 13. Week09 - Lec02 - Binary Search Trees
- 14. Week10 - Lec01 - Splay Trees
01. Week01 - Lec02 - Revision and setting the scene
- C语言除法只有一个符号,与 Python 不同,如果想要得到 float 类型,首先变量需要为 float,另外就是 除数 或者 被除数 之一是 float 类型
如果变量为 int,则自动获取整数部分,不管 除数 与 被除数 是否为 float- float a = 10.0/3, a = 3.333333
- int a = 10.0/3, a = 3
- float a = 10.0/3, a = 3.333333
- Array 可以通过下面方式声明
- int fac[20]; //对于每个元素具体赋值
- int v[5] = {1, 2, 3, 4, 5}; //直接赋值的话,需要加上大括号
- int fac[20]; //对于每个元素具体赋值
- 字符数组需要保留最后为'\0'
- char s[6] = {'h', 'e', 'l', 'l', 'o'};
- char t[6] = "hello";
- char s[6] = {'h', 'e', 'l', 'l', 'o'};
- 数组作为函数参数的时候,同时需要加入数组的长度
- int sumArray(int harry[], int length) {...}
- or
- int sumArray(int *harry, int length) {...}
其中 Harry[] 与 *harry 可以达到一样的效果
- int sumArray(int harry[], int length) {...}
- 二维数组可以看成数组的数组
- m[2][3] 包含2个元素,每个元素都有一个包含3个元素的数组
- m[0] 包含 m[0][0], m[0][1], m[0][2],第1行
- m[1] 包含 m[1][0], m[1][1], m[1][2],第2行
- int m[2][3] = {{1, 2, 3}, {4, 5, 6}};
m[3][2][4] 包含3个元素,其中每个元素一个2*4的数组
分层,最外层3个元素,然后一层是2个元素,最里面是4个元素- int m[3][2][4] = {{{1, 2, 3, 4}, {5, 6, 7, 8}},
- {{9, 10, 11, 12}, {13, 14, 15, 16}},
- {{17, 18, 19, 20}, {21, 22, 23, 24}}};
- m[2][3] 包含2个元素,每个元素都有一个包含3个元素的数组
- struct date {...};
其中 struct date 本身是一个新的数据类型,因此定义新的变量需要这样:
struct date birthday; - #define 用来定义常量
typedef 用来将数据类型重命名
注意,前面有符号的,后面没有分号,前面没有符号的,后面需要分号- #define MAX 20
- typedef struct date Date;
- typedef float Real;
- typedef struct {
- int day, month, year;
- } Date;
- Date birthdays[MAX]; // an array of structs
- #define MAX 20
- 结构体访问
- structTypeName s, *sp;
- sp = &s;
- s.element
- (*sp).element
- sp->element
- structTypeName s, *sp;
- int main(int argc, char *argv[])
- argc: number of arguments
- argv[]: allow access to arguments represented as strings
- atoi(Origin_string): string to number
- sscanf(Origin_string, "%d", &num): string to everything(num)
- int main(int argc, char *argv[])
02. Week02 - Lec01 - Data structures - memory allocation
- a char takes 1 byte (8 bits)
an int takes 4 bytes (32 bits)
a pointer takes 8 bytes (64 bits) (64 bit computers)
sizeof structs
组成 8 bytes,无法组成的就空缺,可以设想成 8 bytes 一个卡壳,而且按顺序放- struct s1 {
- char c;
- int i;
- char *s;
- };
其中 1 + 4 (+ 3) + 8 = 16
- struct s2 {
- char c;
- char *s;
- int i;
- };
其中 1 (+ 7) + 8 + 4 (+4) = 24
- struct s1 {
03. Week02 - Lec02 - Input - Output
- 3 main sources of input for programs:
from the command line: argc, argv[]
from standard input (also called stdin)
stdin can be the keyboard, a data file, or the output of other program
from an 'internally-defined' file
open a file, use fscanf(), and don't forget to close the file - command line
sscanf(argv[1], "%d", &num) != 1
如果赋值成功的话,会返回赋值的个数,将字符串 argv[1] 转换为 数字 num - standard input (stdin)
- scanf("%d", &num) != 1
- or
- scanf("%d%d, &num1, &num2) != 2 //表示两个数字,中间可以间隔whitespace
没有 string 参数,直接获取 stdin 的信息,或者是输入的,或者是文件
pipe command: |, 将前一个输出当做后一个输入使用 getchar()
一次获取一个字符,检测是否到达 '\n'- char c = getchar();
- while (c != '\n') {...}
- scanf("%d", &num) != 1
- a user file
fopen(), fscanf(), fclose() - stdout, stderr
fprinf(stream, ...)
stdin: scanf()
stdout: printf() - scanf(): to read from stdin,只能读取 keyboard 或者 文件,与 printf 对应
多个含有空格的字符,无线调用 scanf 可以读取数字
sscanf(): to read from the command line,从字符串获取信息
printf(): to write to stdout,只能输出到控制台 或者 文件
fprintf(): to write to stderr
04. Week03 - Lec01 - ADTs
- 实现 struct
- typedef struct point {
- float x;
- float y;
- } *Point;
struct point 用来计算 malloc 中空间大小
Point 以指针形式,可以直接修改地址对应的数据- Point p;
- p = malloc(sizeof(struct point));
- p->x
- p->y
- typedef struct point {
- Stacks and queues
stacks: Last in, first out
通过数组实现,快速简单,不过要固定长度
通过 linkedlist 实现,慢,不过可以灵活增加内存
a postfix calculator
queues: First in, first out
‘circular’ queue
数组实现:
stacks:尾部push,尾部pop
queues:头部qush,尾部pop
05. Week03 - Lec02 - Dynamic memory allocation
- 声明的变量放在 stack 里面
malloc 的内存空间放在 heap 里面 - For every malloc() there should be a corresponding free()
when free'd, that heap space may be re-used by the system
free(p);
p = NULL; - When a program teminates, all memory the program uses is automatically freed.
It is not dangerous to forget to free memory at the end of a program,
but it's poor style. Sometimes it's dangerous. - Realloc
If the space returned by a malloc() is too little, you can create more by calling realloc().- char *p = malloc(SIZEINBYTES)
- .
- .
- char *pext = realloc(p, BIGGERSIZEINBYTES);
- .
- .
- char *p = malloc(SIZEINBYTES)
06. Week04 - Lec01 - LinkedLists
- 与数组相比的优点:
- 动态分配空间,可以是任意大小
- 数组需要连续的空间,不好把控
- 更容易删除节点
- 与数组相比的缺点:声明:
- 不能随机访问,数组可以
- 只能连续访问,但是数组更快
- 操作量更大
- 每个元素都有一个额外的指针
- Sedgwick
- typedef struct node *Link;
- struct node{
- int data;
- Link next;
- }
Albert
- typedef struct node {
- int data;
- struct node *next;
- } List;
- 通过 LinkedList 来实现 Quack
- push:将 node 放在 head 之后,就是最前面
- qush:需要找到最后一个节点,然后直接连接上
- pop:Quack qs,qs 不能是 NULL,不能使 Empty, 删除第一个 node 并且释放
- destroyQuack:释放出 head 之外的所有节点
- makeEmptyQuack:pop 掉所有节点
- isEmptyQuack:是否头节点指向 NULL
- showQuack:按顺序输出 data
- Head nodeA linkedlist ADT interface
- 创建出来的
- 存储的是 dummy data,最大值,没意义
- 不能被删除,不是 linkedlist 信息内容
- 如果 quack 为空,指向 NULL
- 如果 quack 不为空,指向 top node
- 返回 head node 给 client
- typedef struct node *List;
...
因此 interface 里面可以用到 List - A linkedlist ADT
- struct node {
- int data;
- struct node *Next;
- };
- ...
因此 ADT 里面可以用访问结构体内部信息
- struct node {
07. Week06 - Lec01 - Heaps
- heap memory
- a programmer can request heap memory by using malloc()
- the memory is 'returned' to the heap by using free()
- heap data structure
- higher-level than array and linked list
- a heap data structrue is built on an array, or linked list
- two-dimensional because it forms a tree of data
- a binary tree (at most 2 children per node)
- higher-level than array and linked list
- Max-heaps
- the element with the largest key is at the root
- the children of a node have keys smaller than the parent
- Min-heaps
- the element with the smallest key is at the root
- the children of a node have keys larger than the parent
- 2 properties
- HOP (Heap-Order Property): 子节点的值比父节点小或者大
- CTP (Complete-Tree Property): 完全二叉树,可以保证子节点与父节点的位置是2倍关系
- heaps 用来实现 priority queues,使用在最短路径算法
- Heap Implementation
- 根节点索引值为 1
- 给定节点索引 i:
- 它的左节点是 2i
- 它的右节点是 2i + 1
- 它的父节点是 i/2(使用整数结果)
- Operation on heaps
- Get the maximum element
- 根节点,位置 1
- Insert an element
- 把新要素放到最下面最右边的位置,放在数组的最后
- fixUp:随着单一路径向根部传递,按照 Heap-Order Property
- Delete the maximum element
- delMax 大根堆
- delMin 小根堆
- 删除叶子节点,可以直接操作
- 删除根节点
- 删除root,将最后的元素替换掉,并将其删除,然后
- fixDown from the root (Heap-Order Property)
- return the saved root node
- fixDown:随着单一路径从根部向叶子节点传递
- Get the maximum element
08. Week06 - Lec02 - Priority Queues and Heap Sort
- A priority queue supports 2 abstract operations:
- insert: a new item (push, qush)
- delMax (pop)
- A Priority Queue ADT
- insertPQ:通过 fixUp,构建大根堆
- delMaxPQ:删掉第一个值,然后执行 fixDown
- Three implementations of the PQ ADT
- an unordered array
- struct pqRep {
- int nItems; // actual count of Items
- int *items; // array of Items
- int maxsize; // maximum size of array
- };
- struct pqRep {
- 插入数据,放置在最后
- 删除最大值,通过遍历来获取
- an ordered array
- 插入数据,查找数据按照顺序的位置,然后将后面的数据逐个后移,将数据插入
- 删除最大值,就是最后一个元素
- a heapified array
- 插入数据,调用 fixUp,将数据进行排序
- 删除最大值,删除一个元素,最后一个元素补入,通过 fixDown 操作
- an unordered array
09. Week07 - Lec01 - Graphs
- Complete graph
- 任何两点都有相连的边
- |E| = V(V-1)/2 (排列组合里面 V 个顶点,里面随机选取 2 个的可能性)
- Clique
- a complete subgraph
- a subset of vertices that form a complete graph
- Sparseness/denseness of a gragh
- dense graphs: |E| is closer to V(V-1)/2
- sparse graphs: |E| is closer to V (minimum is V-1)
- Tree
- a connected (sub)graph with no cycles
- Spanning Tree
- a tree that contains all vertices in the graph (可以是所有孤立的点,只删除 edges,点集不变)
- 包含所有 graph 中顶点的 tree,例如 最小生成树
- Terminology
- graph;顶点集与边集
- subgraph:顶点集与边集都是 上面graph 的子集
- induced subgraph:导出子图,顶点集是子集(只删除顶点的子集,相连的边会自动删除)
ref: https://www.youtube.com/watch?v=dPHkyRvLtIU - cycle:首尾相接
- connected graph:连接所有顶点的路径
- adjacency:两个相连接的顶点
- degree:一个顶点与其相连的顶点个数
- Hamiltonian path and cycle
- 每个顶点只访问一次,path
- 如果首尾相接,cycle(所有顶点的degree >= n/2)
- Eulerian path and cycle
总结:- 遍历每条边正好一次,path(恰好只有2个顶点有奇数的degree)
- 如果收尾相接,cycle(所有的顶点都是偶数的degree)
- 两者都不是:看奇数degree顶点个数,如果1个或者大于2个,都是没有的
- 1. 不可能同时有欧拉path或者cycle
2. 有Hamiltonian cycle一定有path
3. 判断H 回路 的方法就是所有顶点的度都≥n/2
4. 判断欧拉path:只有两个是奇数的度
5. 判断欧拉cycle:所有都为偶数的度 - 其他
- Undirected Graphs
- edge(u, v) = edge(v, u)
- no self-loops (i.e. no edge(v, v))
- Directed Graphs
- edge(u, v) ≠ edge(v, u)
- can have self-loops (i.e. edge(v, v))
- Weighted Graphs
- 有权值的
- road map
- Multi-graph
- 两个顶点间可以拥有多条边相连
- 去一个地方的不同方式,线路等
- Undirected Graphs
- Implementing Graphs
- Vertex that is represented by an int
- Edge that is represented by 2 vertices
- Graph that is represented by an Adjacency matrix, or as an Adjacency list.
- building:
create a graph
create an edge
add an edge to a graph
deleting
remove an edge from a graph
remove and free a graph
printing
'show' a graph - Edge
- typedef int Vertex; // define a VERTEX
- typedef struct { // define an EDGE
- Vertex v;
- Vertex w;
- } Edge;
- GraphAM.c: based on an Adjacency Matrix
- struct graphRep {
- int nV; // #vertices
- int nE; // #edges
- int **edges; // matrix of Booleans ... THIS IS THE ADJACENCY MATRIX
- };

- GraphAL.c: based on an Adjacency Linked List
- typedef struct node *List;
- struct node {
- Vertex name;
- List next;
- };
- struct graphRep {
- int nV; // #vertices
- int nE; // #edges
- List *edges; // array of linked lists ... THIS IS THE ADJACENCY LIST
- };

- insertEdge: 两个顶点都要加,并且是插入到头部的位置
- Reading a graph
- scanf("%d", &v) != EOF,说明没有读取到文件结尾
- scanf("%d", &v) != '\n',说明没有读取到换行符
- scanf 会自动跳过空格、制表符或者回车
- int readNumV(void) { // returns the number of vertices numV or -1
- int numV;
- char w[WHITESPACE];
- scanf("%[ \t\n]s", w); // skip leading whitespace
- if ((getchar() != '#') ||
- (scanf("%d", &numV) != 1)) {
- fprintf(stderr, "missing number (of vertices)\n");
- return -1;
- }
- return numV;
- }
- int readGraph(int numV, Graph g) { // reads number-number pairs until EOF
- int success = true; // returns true if no error
- int v1, v2;
- while (scanf("%d %d", &v1, &v2) != EOF && success) {
- if (v1 < 0 || v1 >= numV || v2 < 0 || v2 >= numV) {
- fprintf(stderr, "unable to read edge\n");
- success = false;
- }
- else {
- insertEdge(newEdge(v1, v2), g);
- }
- }
- return success;
- }
10. Week07 - Lec02 - Graph search
- Depth-first search (BFS)
- stack
- //HANDLES CONNECTED GRAPHS ONLY
- void dfsQuack(Graph g, Vertex v, int numV) {
- int *visited = mallocArray(numV);
- Quack s = createQuack();
- push(v, s);
- showQuack(s);
- int order = 0;
- while (!isEmptyQuack(s)) {
- v = pop(s);
- if (visited[v] == UNVISITED) { // we visit only unvisited vertices
- printArray("Visited: ", visited, numV);
- visited[v] = order++;
- for (Vertex w = numV - 1; w >= 0; w--) { //push adjacent vertices
- if (isEdge(newEdge(v,w), g)) { // ... in reverse order
- push (w, s); // ... onto the stack
- }
- }
- }
- showQuack(s);
- }
- printArray("Visited: ", visited, numV);
- free(visited);
- return;
- }
- dfsQuack() (disconnected graphs)
- 设置一个参数 allVis,判断是否全部顶点都访问了
- //HANDLES CONNECTED GRAPHS ONLY
- void dfsQuack(Graph g, Vertex v, int numV) {
- int *visited = mallocArray(numV);
- Quack s = createQuack();
- push(v, s);
- showQuack(s);
- int order = 0;
- while (!isEmptyQuack(s)) {
- v = pop(s);
- if (visited[v] == UNVISITED) { // we visit only unvisited vertices
- printArray("Visited: ", visited, numV);
- visited[v] = order++;
- for (Vertex w = numV - 1; w >= 0; w--) { //push adjacent vertices
- if (isEdge(newEdge(v,w), g)) { // ... in reverse order
- push (w, s); // ... onto the stack
- }
- }
- }
- showQuack(s);
- }
- printArray("Visited: ", visited, numV);
- free(visited);
- return;
- }
- Recursive Depth-First Search
- 包含了 disconnected graphs 的情况,另外函数内部加入指针,可以改变地址同时相当于全局变量
- void dfs(Graph g, Vertex rootv, int numV) {//'wrapper' for recursive dfs
- int *visited = mallocArray(numV); // ... handles disconnected graphs
- int order = 0;
- Vertex startv = rootv; // this is the starting vertex
- int allVis = 0; // assume not all visited
- while (!allVis) { // as long as there are vertices
- dfsR(g, startv, numV, &order, visited);
- allVis = 1; // are all visited now?
- for (Vertex w = 0; w < numV && allVis; w++) { // look for more
- if (visited[w] == UNVISITED) {
- printf("Graph is disconnected\n"); // debug
- allVis = 0; // found an unvisited vertex
- startv = w; // next loop dfsR this vertex
- }
- }
- }
- printArray("Visited: ", visited, numV);
- free(visited);
- return;
- }
- void dfsR(Graph g, Vertex v, int numV, int *order, int *visited) {
- visited[v] = *order; // records the order of visit
- *order = *order+1;
- for (Vertex w = 0; w < numV; w++) {
- if (isEdge(newEdge(v,w), g) && visited[w]==UNVISITED) {
- dfsR(g, w, numV, order, visited);
- }
- }
- return;
- }
- Breadth First Search
- queue
- void bfsQuack(Graph g, Vertex v, int numV) { //name change
- int *visited = mallocArray(numV);
- Quack q = createQuack();
- qush(v, q); //qush, not push
- showQuack(q);
- int order = 0;
- while (!isEmptyQuack(q)) {
- v = pop(q);
- if (visited[v] == UNVISITED) {
- printf("Visit %d\n", v); // debug
- visited[v] = order++;
- for (Vertex w = 0; w < numV; w++) {//vertex order
- if (isEdge(newEdge(v,w), g)) {
- qush(w, q); //qush, not push
- }
- }
- }
- showQuack(q);
- }
- printArray("Visited: ", visited, numV);
- free(visited);
- makeEmptyQuack(q);
- return;
- }
11. Week08 - Lec02 - Applications of Graph Search
- Breadth-First Search: Shortest path
- ref: https://www.cnblogs.com/alex-bn-lee/p/11242024.html#A42
- void shortestPath(Graph g, Vertex start, Vertex goal, int numV) {
- int *visited = mallocArray(numV);
- int *parent = mallocArray(numV); // THIS IS NEW
- Quack q = createQuack();
- qush(start, q);
- int order = 0;
- visited[start] = order++;
- int found = 0;
- while (!isEmptyQuack(q) && !found) { // FOUND TELLS US TO STOP
- Vertex v = pop(q);
- for (Vertex w = 0; w < numV && !found; w++) {
- if (isEdge(newEdge(v,w), g)) { // for adjacent vertex w ...
- if (visited[w] == UNVISITED) { // ... if w is unvisited ...
- qush(w, q); // ... queue w
- printf("Doing edge %d-%d\n", v, w); // DEBUG
- visited[w] = order++; // w is now visited
- parent[w] = v; // w's PARENT is v
- if (w == goal) { // if w is the goal ...
- found = 1; // ..FOUND IT! NOW GET OUT
- }
- }
- }
- }
- }
- if (found) {
- printf("SHORTEST path from %d to %d is ", start, goal);
- printPath(parent, numV, goal); // print path from START TO GOAL
- putchar('\n');
- }
- else {
- printf("no path found\n");
- }
- printArray("Visited: ", visited, numV); // debug
- printArray("Parent : ", parent, numV); // debug
- free(visited);
- free(parent);
- makeEmptyQuack(q);
- return;
- }
- // head recursion
- void printPath(int parent[], int numV, Vertex v) {
- if (parent[v] != UNVISITED) { // parent of start is UNVISITED
- if (0 <= v && v < numV) {
- printPath(parent, numV, parent[v]);
- printf("-->");
- }
- else {
- fprintf(stderr, "\nprintPath: invalid goal %d\n", v);
- }
- }
- printf("%d", v); // the last call will print here first
- return;
- }
- // head recursion
- void printPath(int parent[], int numV, Vertex v) {
- printf("%d", v);
- if (0<=v && v<numV) {
- Vertex p = parent[v];
- while (p != UNVISITED) {
- printf("<--%d", p);
- p = parent[p];
- }
- }
- else {
- fprintf(stderr, "printPath: illegal vertex in parent[]\n");
- }
- }
- void printPath(int parent[], int numV, Vertex v) {
- Depth-First Search: Cycle detection
- ref: https://www.cnblogs.com/alex-bn-lee/p/11242024.html#A43
- // a wrapper for the recursive call to hasCycle()
- void searchForCycle(Graph g, int v, int numV) {
- int *visited = mallocArray(numV);
- int order = 0;
- if (hasCycle(g, numV, v, v, &order, visited)) {
- printf("found a cycle\n");
- }
- else {
- printf("no cycle found\n");
- }
- printArray("Visited ", visited, numV);
- free(visited);
- return;
- }
- int hasCycle(Graph g, int numV, Vertex fromv, Vertex v, int *order, int *visited) {
- int retval = 0;
- visited[v] = *order;
- *order = *order+1;
- for (Vertex w = 0; w < numV && !retval; w++) {
- if (isEdge(newEdge(v,w), g)) {
- if (visited[w] == UNVISITED) {
- printf("traverse edge %d-%d\n", v, w);
- retval = hasCycle(g, numV, v, w, order, visited);
- }
- else {
- if (w != fromv) { // exclude the vertex we've just come from
- // WE HAVE REVISITED A VERTEX ==> CYCLE
- printf("traverse edge %d-%d\n", v, w);
- retval = 1;
- }
- }
- }
- }
- return retval;
- }
- Depth-First Search: Eulerian cycles
- https://www.cnblogs.com/alex-bn-lee/p/11242024.html#A44
- void findEulerianCycle(Graph g, int numV, Vertex startv) {
- Quack s = createQuack();
- printf("Eulerian cycle: ");
- push(startv, s);
- while (!isEmptyQuack(s)) {
- Vertex v = pop(s); // pop and then ...
- push(v, s); // ... push back on, so no change
- Vertex w = getAdjacent(g, numV, v); // get largest adj. v
- if (w >= 0) { // if true, there is an adj. vertex
- push(w, s); // push this vertex onto stack
- removeEdge(newEdge(v, w), g); // remove edge to vertex
- }
- else { // top v on stack has no adj. vertices
- w = pop(s);
- printf("%d ", w);
- }
- }
- putchar('\n');
- }
- Vertex getAdjacent(Graph g, int numV, Vertex v) {
- Vertex retv = -1; // assume no adj. vertices
- for (Vertex w = numV-1; w >= 0 && retv == -1; w--) {
- if (isEdge(newEdge(v, w), g)) {
- retv = w; // found largest adj. vertex
- }
- }
- return retv;
- }
- Depth-First Search: Finding a path
- https://www.cnblogs.com/alex-bn-lee/p/11242024.html#A45
- void dfsR(Graph g, Vertex v, int numV, int *order, int *visited) {
- visited[v] = *order;
- *order = *order+1;
- for (Vertex w = 0; w < numV; w++) {
- if (isEdge(newEdge(v,w), g) && visited[w]==UNVISITED) {
- dfsR(g, w, numV, order, visited);
- }
- }
- return;
- }
- int isPath(Graph g, Vertex v, Vertex goalv, int numV, int *order, int *visited) {
- int found = 0;
- visited[v] = *order;
- *order = *order+1;
- if (v == goalv) {
- found = 1;
- }
- else {
- for (Vertex w = 0; w < numV && !found; w++) {
- if (isEdge(newEdge(v,w), g)) {
- if (visited[w] == UNVISITED) {
- found = isPath(g, w, goalv, numV, order, visited);
- printf("path %d-%d\n", w, v);
- }
- }
- }
- }
- return found;
- }
- void dfsR(Graph g, Vertex v, int numV, int *order, int *visited) {
12. Week09 - Lec01 - Weighted Graph Algorithms
- Dijkstra 算法
- Prim 算法Kruskal 算法
- Firefox 崩溃了,数据丢了,坑爹~
13. Week09 - Lec02 - Binary Search Trees
- Height:具体根节点的高度,root 为 0
- Node level or depth:跟 Height 差不多
- Types of trees
- ordered tree: 有序树
- binary tree: 二叉树
- full binary tree: 满二叉树,每个节点都有2个孩子,可能参差不齐
- perfect binary tree: 完美二叉树,类似三角形那种,都铺满了
- ordered binary tree:有序二叉树,也叫做 binary search tree,二叉搜索树
- left subtree values <= parent value
- right subtree values >= parent value
- full m-ary tree: 类似满二叉树
- Binary Trees
- balanced:尽量满,最短的
- degenerate:退化的,一边倒,最长的
- Height of a binary tree
- 最长路径的长度
- degenerate: height is n-1
- balanced: height is ln(n)
- Data structure for a binary tree
- typedef struct node *Tree;
- struct node {
- int data;
- Tree left;
- Tree right;
- };
- typedef struct node *Tree;
- Comparing Binary Search Trees and Heaps
Searching in BSTs
- 结束条件就是 顶点 为 NULL,返回 0,或者查到了 v 值,返回 1
- int searchTree(Tree t, int v){ // Search for the node with value v
- int ret = 0;
- if (t != NULL) {
- if (v < t->data) {
- ret = searchTree(t->left, v);
- }
- else if (v > t->data) {
- ret = searchTree(t->right, v);
- }
- else { // v == t->data
- ret = 1;
- }
- }
- return ret;
- } // returns non-zero if found, zero otherwise
- int searchTree(Tree t, int v){ // Search for the node with value v
Creating a node in a BST
- 构建结构体,建立数,结构体是一个 node 点,但是树是一个指针 Tree,连接着所有的点
- 创建树,首先就是分配内存空间,然后就是赋值
默认左右节点都为 NULL - typedef struct node *Tree;
- struct node {
- int data;
- Tree left;
- Tree right;
- };
- Tree createTree(int v) {
- Tree t;
- t = malloc(sizeof(struct node));
- if (t == NULL) {
- fprintf(stderr, "Out of memory\n");
- exit(1);
- }
- t->data = v;
- t->left = NULL;
- t->right = NULL;
- return t;
- }
- typedef struct node *Tree;
- Freeing a node in a BST
- 结束条件就是遇到叶子节点,因为其左右节点均为 NULL
- void freeTree(Tree t) { // free in postfix fashion
- if (t != NULL) {
- freeTree(t->left);
- freeTree(t->right);
- free(t);
- }
- return;
- }
- void freeTree(Tree t) { // free in postfix fashion
- Inserting a node in a BST
- 重点是返回值是 Tree
结束条件就是遇到叶子节点,因为其左右节点均为 NULL,因此会创建新的 node 点,然后将值依次返回
由于返回值为 Tree,因此自动连接的起来 - Tree insertTree(Tree t, int v) {
- if (t == NULL) {
- t = createTree(v);
- }
- else {
- if (v < t->data) {
- t->left = insertTree (t->left, v);
- }
- else {
- t->right = insertTree (t->right, v);
- }
- }
- return t;
- }
- Tree insertTree(Tree t, int v) {
- do it iteratively
- 通过遍历找到对应的叶子节点,然后连接上 node
- Tree insertTreeI(Tree t, int v) { // An iterative version of the above
- if (t == NULL) {
- t = createTree(v);
- }
- else { // t != NULL
- Tree parent = NULL; // remember the parent to link in new child
- Tree step = t;
- while (step != NULL) { // this is the iteration
- parent = step;
- if (v < step->data) {
- step = step->left;
- }
- else {
- step = step->right;
- }
- } // step == NULL
- if (v < parent->data) {
- parent->left = createTree(v);
- }
- else {
- parent->right = createTree(v);
- }
- }
- return t;
- }
- Tree insertTreeI(Tree t, int v) { // An iterative version of the above
- 重点是返回值是 Tree
- Printing the tree
- 遍历打印,先左 再中 后右
- void printTree(Tree t) { // not the final version
- if (t != NULL) {
- printTree (t->left);
- printf ("%d ", t->data);
- printTree (t->right);
- }
- return;
- }
- void printTree(Tree t) { // not the final version
- 2D printing
- 每次递归,depth 自增,打印数据的时候,先将制表符打印出来,出现层次感
- void printTree(Tree t, int depth) { // extra depth parameter
- if (t != NULL) {
- depth++;
- printTree (t->left, depth);
- for (int i=1; i<depth; i++){ // 'depth'*whitespace
- putchar('\t');
- }
- printf ("%d\n", t->data); // node to print
- printTree (t->right, depth);
- }
- return;
- }
- void printTree(Tree t, int depth) { // extra depth parameter
- 反方向打印
- void printTree2(Tree t, int depth) {
- if (t != NULL) {
- depth++;
- printTree2 (t->right, depth);
- int i;
- for (i=1; i<depth; i++){
- putchar('\t');
- }
- printf ("%d\n", t->data);
- printTree2 (t->left, depth);
- }
- return;
- }
- void printTree2(Tree t, int depth) {
- 效果如下:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- ====================================
- 8
- 7
- 6
- 5
- 4
- 3
- 2
- 1
- 1
- Count the number of nodes in a BST
- 遍历相加,每个节点为 1
结束条件就是叶子节点,因为其左右节点均为 NULL,自动返回 1,然后不停回溯。。 - int count(Tree t){
- int countree = 0;
- if (t != NULL) {
- countree = 1 + count(t->left) + count(t->right);
- }
- return countree;
- }
- int count(Tree t){
- 遍历相加,每个节点为 1
- Find the height of a BST
- 对于叶子节点本身,高度为 0,因此 NULL 节点的高度就为 -1
parent 节点的高度 = 1 + MAX (left height, right height) - int max(int a, int b){
- if (a >= b) {
- return a;
- }
- return b;
- }
- int height(Tree t){
- int heightree = -1;
- if (t != NULL){
- heightree = 1 + max(height(t->left), height(t->right));
- }
- return heightree;
- }
- int max(int a, int b){
- 对于叶子节点本身,高度为 0,因此 NULL 节点的高度就为 -1
- How balanced is a BST?
How do the number of nodes in the left sub-tree and the right sub-tree compare?- 分别计算出左右子树的节点数,然后相减即可
- int balance (Tree t){ // calculates the difference between left and right
- int diff = 0;
- if (t != NULL) {
- diff = count(t->left) - count(t->right); // count declared elsewhere
- if (diff < 0) {
- diff = –diff;
- }
- }
- return diff;
- }
- int balance (Tree t){ // calculates the difference between left and right
- Deleting a node from a BST
- 3 cases
- node is a leaf: unlink node from parent
- node has 1 child: replace the node by its child
- node has 2 children: rearrange the tree in some way
- DLMD: Deepest Left-Most Descendent
- DRMD: Deepest Right-Most Descendent
- 把 DLMD 摘下来,左边连接 t1,右边连接 t2
DLMD 为最左,因此其次需要将其 parent 节点的 left 与 DLMD 的 right 相连
p->left = nuroot->right
注意需要保留 DLMD 的 parent 节点 - Tree deleteTree(Tree t, int i){ // delete node with value 'v'
- if (t != NULL) {
- if (v < t->data) {
- t->left = deleteTree(t->left, v);
- }
- else if (v > t->data) {
- t->right = deleteTree(t->right, v);
- }
- else { // v == t->data, so the node 't' must be deleted
- // next fragment of code violates style, just to make logic clear
- Tree n; // temporary
- if (t->left==NULL && t->right==NULL) n=NULL; // 0 children
- else if (t->left ==NULL) n=t->right; // 1 child
- else if (t->right==NULL) n=t->left; // 1 child
- else n=joinDLMD(t->left,t->right);
- free(t);
- t = n;
- }
- }
- return t;
- }
- Tree deleteTree(Tree t, int i){ // delete node with value 'v'
- // Joins t1 and t2 with the deepest left-most descendent of t2 as new root.
- Tree joinDLMD(Tree t1, Tree t2){
- Tree nuroot;
- if (t1 == NULL) { // actually should never happen
- nuroot = t2;
- }
- else if (t2 == NULL) { // actually should never happen
- nuroot = t1;
- }
- else { // find the DLMD of the right subtree t2
- Tree p = NULL;
- nuroot = t2;
- while (nuroot->left != NULL) {
- p = nuroot;
- nuroot = nuroot->left;
- } // nuroot is the DLMD, p is its parent
- if (p != NULL){
- p->left = nuroot->right; // give nuroot's only child to p
- nuroot->right = t2; // nuroot replaces deleted node
- }
- nuroot->left = t1; // nuroot replaces deleted node
- }
- return nuroot;
- }
- // Joins t1 and t2 with the deepest left-most descendent of t2 as new root.
- 3 cases
14. Week10 - Lec01 - Splay Trees
- Right rotation
- its right child moves to the root's left child the root moves to its right child
- 折下来,parent变成child
- Left rotation
- its left child moves to the root's right child the root moves to its left child
- 翻上去,child变成parent

- 相当于告诉了root,然后获取转折点,第一个是 E 是root,然后获取 C,同理。。
然后就是连接起来即可 - // NOT REAL CODE: CHECKS REQUIRED: ACTUAL CODE BELOW
- Tree rotateR(Tree root) { // old root
- Tree newr = root->left; // newr is the new root
- root->left = newr->right; // old root has new root's right child
- newr->right = root; // new root has old root as right child
- return newr; // return the new root
- }
- // NOT REAL CODE: CHECKS REQUIRED: ACTUAL CODE BELOW
- Tree rotateL(Tree root) { // old root
- Tree newr = root->right; // newr will become the new root
- root->right = newr->left; // old root has new root's left child
- newr->left = root; // new root has old root as left child
- return newr; // return the new root
- }
- // NOT REAL CODE: CHECKS REQUIRED: ACTUAL CODE BELOW
- root insertion
assume that we have just inserted node G in the BST below
rotate right the subtree with root the parent of G (i.e. H)
rotate right the subtree with root the parent of G (i.e. R)
rotate left the subtree with root the parent of G (i.e. E)

- 一次只是转一次,保证 G 不停向上走
- Counting the number of nodes in a subtree
- typedef struct node *Tree;
- struct node {
- int data;
- Tree left;
- Tree right;
- int count;
- };
- Tree createTree(int v) {
- Tree t = malloc (sizeof(struct node));
- if (t == NULL) {
- fprintf(stderr, "Out of memory\n");
- exit(1);
- }
- t->data = v;
- t->left = NULL;
- t->right = NULL;
- t->count = 1;
- return t;
- }
- int sizeTree(Tree t) {
- int retval = 0;
- if (t != NULL){
- retval = t->count;
- }
- return retval;
- }
- Tree insertTree(Tree t, int v) {
- if (t == NULL) {
- t = createTree(v);
- }
- else {
- if (v < t->data) {
- t->left = insertTree (t->left, v);
- }
- else {
- t->right = insertTree (t->right, v);
- }
- t->count++; // update the counter at each ancestor
- }
- return t;
- }
- typedef struct node *Tree;
- Selecting the i-th element from a BST
获取某一索引的节点值
类似数组里面 arr[3] 的意思
Balanced Trees- check the number of nodes in the left subtree
- if the left subtree contains numOnLeft elements, and
- numOnLeft>i, we recursively look in this left subtree for element i, else if
- numOnLeft<i, we recursively look in the right subtree for element i-(numOnLeft+1), else if
- numOnLeft=i, return with the current element's data
- if the left subtree contains numOnLeft elements, and

- 如果在左子树直接递归
如果在右子树,需要减掉所有左子树+root的节点数 - // For tree with n nodes – indexes are 0..n-1
- int selectTree(Tree t, int i) { // for tree with n nodes - indexed from 0..n-1
- int retval = 0;
- if (t != NULL) {
- int numOnLeft = 0; // this is if there is no left branch
- if (t->left != NULL) {
- numOnLeft = t->left->count; // this is if there is a left branch
- }
- if (numOnLeft > i) { // left subtree or ...
- retval = selectTree(t->left, i);
- }
- else if (numOnLeft < i) { // ... right subtree ?
- retval = selectTree(t->right, i-(numOnLeft+1));
- }
- else {
- retval = t->data; // value index i == numOnLeft
- }
- }
- else {
- printf("Index does not exist\n");
- retval = 0;
- }
- return retval;
- }
- // For tree with n nodes – indexes are 0..n-1
- check the number of nodes in the left subtree
- Approach 1: Global rebalancing
- Rotating with a count
- Example of left rotation

- 算法与上面一致,只是增加了 count 的计算
对于 E 的count就是等于前面 A 的count
对于 A 的count就直接计算他的左右节点 - Tree rotateLeft(Tree t) { // Rotate left code: includes count field
- Tree retval = NULL;
- if (t != NULL) {
- Tree nuroot = t->right; // left rotate: hence right root-child will become new root
- if (nuroot == NULL) {
- retval = t;
- }
- else {
- t->right = nuroot->left; // the left child of nuroot becomes old root's right child
- nuroot->left = t; // nuroot's left child is the old root
- nuroot->count = t->count; // nuroot and old root have the same count
- t->count = 1 + sizeTree(t->left) + sizeTree(t->right); // recompute count in old root
- retval = nuroot; // return with the new root
- }
- }
- return retval;
- }
- Tree rotateLeft(Tree t) { // Rotate left code: includes count field
- Example of right rotation

- Tree rotateRight(Tree t) { // Rotate right code: includes count field
- Tree retval = NULL;
- if (t != NULL) {
- Tree nuroot = t->left;
- if (nuroot == NULL) {
- retval = t;
- }
- else {
- t->left = nuroot->right;
- nuroot->right = t;
- nuroot->count = t->count;
- t->count = 1 + sizeTree(t->left) + sizeTree(t->right);
- retval = nuroot;
- }
- }
- return retval;
- }
- Tree rotateRight(Tree t) { // Rotate right code: includes count field
- Example of left rotation
- Partitioning,分隔,分区
We can rewrite select() to partition around the ith element in the BST:
- we descend recursively
to the ith element of each subtree
rotate-with-count that element in the opposite direction to its position
if it is a left child: do a right rotation
if it is a right child: do a left rotation
this will make the ith element the root of the BST
- we descend recursively
- 将第 i 个元素作为 root
不停的左右移动 - Tree partition(Tree t, int i) { // make node at index i the root
- Tree retval = NULL;
- if (t != NULL) {
- int numOnLeft = 0;
- if (t->left != NULL) {
- numOnLeft = t->left->count;
- }
- if (numOnLeft > i) {
- t->left = partition(t->left, i);
- t = rotateRight(t);
- }
- if (numOnLeft < i) {
- t->right = partition(t->right, i-(numOnLeft+1));
- t = rotateLeft(t);
- }
- retval = t;
- }
- else {
- printf("Index does not exist\n");
- retval = NULL;
- }
- return retval;
- }
- Tree partition(Tree t, int i) { // make node at index i the root
- Balancing the BST
Approach 2: Local RebalancingMove the median node to the root by partitioning on i = count/2
- balance the left sub-tree
- balance the right sub-tree
- 先把 median 移动到 root
递归移动左右,最终所有的都是 median 在中间 - Tree balance(Tree t) {
- Tree retval = NULL;
- if (t != NULL) {
- if (t->count <= 1){
- retval = t;
- }
- else {
- t = partition(t, t->count/2);
- t->left = balance(t->left);
- t->right = balance(t->right);
- retval = t;
- }
- }
- return retval;
- }
- Tree balance(Tree t) {
Splaying an item to the top means to move an item to the root of the BST, using one of the operations:
zigzag
zigzig
zigzag operation (先下后上)
the item is the right child of the parent, which is a left child of the grandparent
- do a rotate-left of the parent followed by a rotate-right of the grandparent
- /
\ 先是左转parent
/
/ 然后再右转grandparent /\
the item is the left child of the parent, which is a right child of the grandparent
- do a rotate-right of the parent followed by a rotate-left of the grandparent
- \
/ 先是右转parent
\
\ 然后再左转grandparent /\
zigzig operation (先上后下)
the item is the left child of the parent, which is a left child of the grandparent
do a rotate-right of the grandparent followed by a rotate-right of the parent
- (not a rotate-right of the parent followed by a rotate-right of the grandparent
- /
/ 先是右转grandparent /\ 然后再右转parent
\
\
the item is the right child of the parent, which is a right child of the grandparent
do a rotate-left of the grandparent followed by a rotate-left of the parent
- (not a rotate-left of the parent followed by a rotate-left of the grandparent
- \
\ 先是左转grandparent /\ 然后再左转parent
/
/
- Example

H is the right child of the left child so requires a zigzag splay
- this is simply a left-rotate followed by a right-rotate
P is the left child of the right child so requires a zigzag splay
- this is simply a right-rotate followed by a left-rotate
C is the left child of the left child so requires a zigzig splay
a zigzig splay does a right-rotate of the grandparent M, followed by another right-rotate of the parent E
T is the right child of the right child so requires a zigzig splay
a zigzig splay does a left-rotate of the grandparent M, followed by a left-rotate of the parent Q
The first double rotation below is not a zigzig rotation, the second is:
区别在于,第一个图是 先下后上
而 zigzig 是 先上后下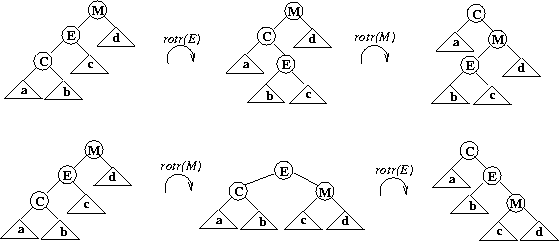
- Operation splay-search
If we search for an item, and move the item to the root by using normal left and right rotations then there is no rebalancing
- for example: a normal search for item 1 would result in
每次移动一个节点,就是 1 不停向上移动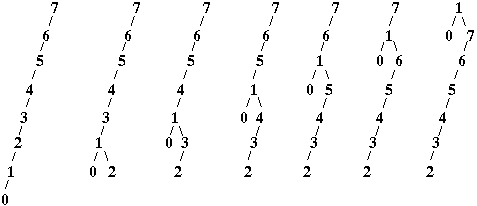
- for example: a normal search for item 1 would result in
If we splay-search for an item, once found we
- splay the item to the root
1作为目标节点,整体是一个左左型,从grandparent右转,然后parent右转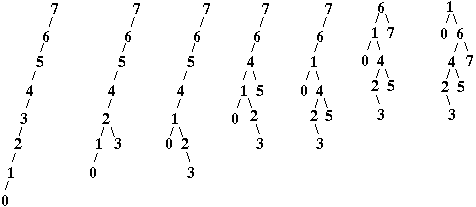
- splay the item to the root
If the item is not found
- the last item (leaf) on the path is splayed to the root
For example, in the following splay tree we search for item 3, and because it fails, the 'last' item accessed, which is 4, is splayed:
找3,结果找到了4,那就移动4,就是判断点是否为叶子节点,是的话就动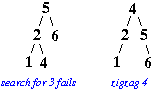
- Operation splay-insertion
- We have seen 2 types of BST insertion, leaf insertion and root insertion. Assume that we wish to insert the sequence of numbers 3, 2, 4, 5, 1.
leaf insertion
- each node is simply added as a leaf
按照 zigzig,zigzag 来操作
分别 先上后下,先下后上
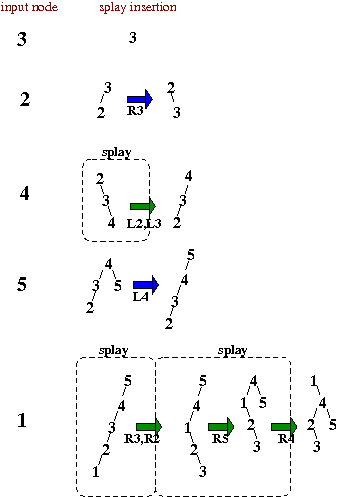
- each node is simply added as a leaf
root insertion
- each node is added as a leaf, and then
- that leaf is promoted to the root position rotating the parent node to the left or right at each step
就是一个一个移动到 root
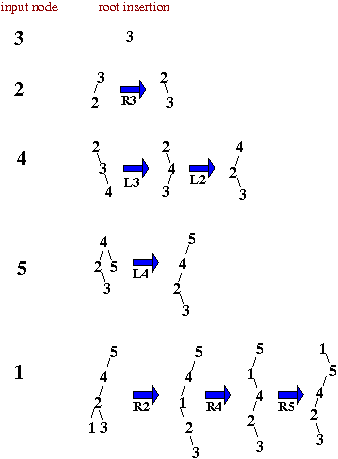
- Operation splay deletion
Normally, when an item is deleted in a BST, the node is simply replaced by its DLMD predecessor or DRMD successor.
In splay-deletion, if you wish to delete a node y:
delete the node y as normal using either:
DRMD: if the predecessor of y is x, and the parent of x is p, then
follow the deletion by splaying p
DLMD: if the successor node of y is z, and the parent of z is p, then
follow the deletion by splaying p
首先把 DLMD 替换 root,然后再将 DLMD 的 parent 移动到 root
For example, let us splay-delete item 2 from the following splay tree
we will use DLMD (DRMD would be similar)
要删除2节点
successor为4,4的父节点是5
把4替换为2节点,作为root
再把5移动上去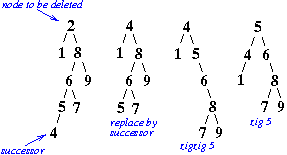
- Minimum or maximum of a splay tree
- search for the minimum or maximum item in a BST
- splay the item to the root
For example, we show below a splay tree after
- a search for the minimum and then
- a search for the maximum item
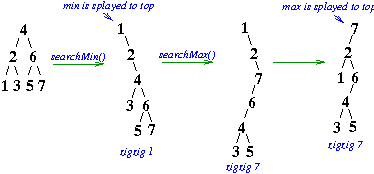

in summary
2-3-4 trees
We note that in each operation:
search for an item in a splay tree
- the found item is splayed
- if not found, the last accessed item is splayed
insertion of an item in a splay tree
- the new item is splayed
deletion of an item in a splay tree
- the parent of the item that replaces the deleted item is splayed
search for the minimum/maximum item in a splay tree
- the found minimum/maximum is splayed
A 'splay' of an item involves:
zigzig whenever the item is left-left or right-right
zigzag whenever the item is left-right or right-left
zig whenever the item is the child of the root (so a zigzag or zigzig is not possible)
Splay Tree Analysis
number of comparisons per operation is O(log(n))
- gives good (amortized) cost overall
no guarantee for any individual operation: worst-case behaviour may still be O(N)
remember, amortisation means averaging over a large number k operations
- is self-balancing
- is commonly used to implement dictionaries
- has the property that all external nodes are at the same depth
- generalises the concept of a node
- 3 types of nodes:
2nodes: 1 key, a left link to smaller nodes, a right link to larger nodes (this is the normal node)
里面只有一个key就是一个字母,类似二叉树,因此只存在大小之分3nodes: 2 keys, a left link to smaller, a middle link to in-between, and right link to larger
里面两个字母,小于,中间,大于三部分4nodes: 3 keys: links to the 4 ranges
三个字母, M O S 分成四个部分

In the above example:
- 'A' is an example of a 2node
- 'LM' of a 3node
- 'EGH' of a 4node
Example of a search, for 'P':
- start at the root 'I'
- larger, go right to 'NR'
- middle, go middle to 'P'
Examples of insertions:
- 'B': easy, change node 'A' into 'AB'
- 'O': easy, change node 'NR' into 'NOR'
'D': the node is full ??
4node insertions
- split the 4node分裂4度节点:
- left key becomes a new 2node 左节点变成一个新的2度节点
- middle key goes up to parent 中间节点上提到parent里面
- right node becomes a new 2node 右节点变成一个新的2度节点
- add new key to one of the new 2nodes, creating a 3node
Example: insert 'D' in a 2-3-4 tree

This insertion assumes that you can move the 'middle' key up to the parent.
What happens if the parent is a 4node, and its parent is a 4node, and its parent ... ?
Solution, during insertion, on the way down:
[A] transform 2node->4node into 3node->(2node+2node)
[B] transform 3node->4node into 4node->(2node+2node)
[C] if the root is a 4node, transform into 2node->(2node+2node)
Example:
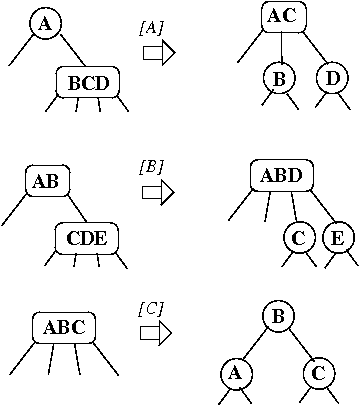
Basic insertion strategy:
because of the transformations (splits) on inserts on the way down, we often end on a 2node or 3node, so easy to insert
- insert at the bottom:
- if 2node or 3node, simply include new key
- if 4node, split the node
4node需要将中间节点上调,上调后parent又需要上调,以此类推
相当于递归了- if the parent is a 4node, this needs to be split
- if the grandparent is a 4node, this needs to be split
- ...
- if the grandparent is a 4node, this needs to be split
- if the parent is a 4node, this needs to be split
Results:
- trees are
split from the top down
(split and) grow from the bottom up
after insertions or deletions, 2-3-4 trees remain in perfect balance
What do you notice about these search trees?
2-3-4 trees are actually implemented using BSTs!
- 3 types of nodes:
【433】COMP9024 复习的更多相关文章
- iOS总结_UI层自我复习总结
UI层复习笔记 在main文件中,UIApplicationMain函数一共做了三件事 根据第三个参数创建了一个应用程序对象 默认写nil,即创建的是UIApplication类型的对象,此对象看成是 ...
- vuex复习方案
这次复习vuex,发现官方vuex2.0的文档写得太简略了,有些看不懂了.然后看了看1.0的文档,感觉很不错.那以后需要复习的话,还是先看1.0的文档吧.
- 我的操作系统复习——I/O控制和系统调用
上篇博客介绍了存储器管理的相关知识——我的操作系统复习——存储器管理,本篇讲设备管理中的I/O控制方式和操作系统中的系统调用. 一.I/O控制方式 I/O就是输入输出,I/O设备指的是输入输出设备和存 ...
- 复习(1)【Maven】
终于开始复习旧知识了,有输入必然要有输出.输入和输出之间的内化过程尤为重要,在复习的同时,真正把学到的东西积淀下来,加深理解. Maven项目概念与配置 Maven是一个项目管理和综合工具.Maven ...
- 《CSS权威指南》基础复习+查漏补缺
前几天被朋友问到几个CSS问题,讲道理么,接触CSS是从大一开始的,也算有3年半了,总是觉得自己对css算是熟悉的了.然而还是被几个问题弄的"一脸懵逼"... 然后又是刚入职新公司 ...
- JS复习--更新结束
js复习-01---03 一 JS简介 1,文档对象模型 2,浏览器对象模型 二 在HTML中使用JS 1,在html中使用<script></script>标签 2,引入外部 ...
- jQuery 复习
jQuery 复习 基础知识 1, window.onload $(function(){}); $(document).ready(function(){}); 只执行函数体重的最后一个方法,事 ...
- jQuery5~7章笔记 和 1~3章的复习笔记
JQery-05 对表单和表格的操作及其的应用 JQery-06 jQuery和ajax的应用 JQery-07 jQuery插件的使用和写法 JQery-01-03 复习 之前手写的笔记.实在懒得再 ...
- HTML和CSS的复习总结
HTML(Hypertext Markup Language)超文本标记语言:其核心就是各种标记!<html> HTML页面中的所有内容,都在该标签之内:它主要含<head>和 ...
随机推荐
- notepad++ 调整行间距
在“设置”-“语言格式设置”里面,找到style里面的Line number margin一项,调整字体大小就可以调整左边标号的大小,然后文本内容的行间距即可任意调整.
- oracle中日期相关的区间
and czrqb.lsrqb_rh_sj >= to_date('[?query_date_begin|2011-09-01?]A', 'yyyy-mm-dd') and czrqb.lsrq ...
- C#技巧与解析(部分)
DesignMode 以下项目在设计器界面,需判断DesignMode OnPaint(e)/Form_Paint 自定义控件中需要特殊方法进行判断,如下: public partial class ...
- 语义(Semantics)
流计算语义(Semantics)的定义 每一条记录被流计算系统处理了几次 有三种语义: 1.At most once 一条记录要么被处理一次,要么没有被处理 2.At least once 一条记录可 ...
- 4.3 axios
axios全局拦截器:
- [React] Write a Custom React Effect Hook
Similar to writing a custom State Hook, we’ll write our own Effect Hook called useStarWarsQuote, whi ...
- 【爬虫】大杀器——phantomJS+selenium
[爬虫]大杀器——phantomJS+selenium 视频地址 江湖上有一个传说,得倚天屠龙者可称霸武林.爬虫中也有两个大杀器,他们结合在一起时,无往不利,不管你静态网站还是动态网站,通吃. pha ...
- Apache Kylin在4399大数据平台的应用
来自:AI前线(微信号:ai-front),作者:林兴财,编辑:Natalie作者介绍:林兴财,毕业于厦门大学计算机科学与技术专业.有多年的嵌入式开发.系统运维经验,现就职于四三九九网络股份有限公司, ...
- mysql 8.0.17 安装配置方法图文教程
1.URL:https://www.jb51.net/article/167782.htm 2.装好之后需要使用add user中的用户名和密码登录(之前安装数据库时出现的) 使用navicat连接时 ...
- windbg调试托管代码 .Net clr
现在很多的程序都是多语言混合编程的,比如我司的产品,就是用C++/.net clr混合编制的.那么当我们调试这样的程序时,一定要注意,比如有时我们只看到c++的栈和名称,而.net clr的代码确看不 ...


