近年NOI题目总结

NOI2015D1T1

题目大意：$T$ 组数据。在一个程序中有无数个变量 $x_i$。现在有 $n$ 条限制，形如 $x_i=x_j$ 或者 $x_i\ne x_j$。（对于每个限制 $i,j$ 给定）问是否存在一种合法的赋值方案满足所有限制。

$1\le T\le 10,1\le n\le 10^5,1\le i,j\le 10^9$。

普及难度。先把所有编号离散化，然后对于每个相等的限制，把这两个变量塞到一个集合里（并查集）。最后对于每个不等的限制，判断两个变量是否在一个集合里。

时间复杂度 $O(Tn\log n)$。

#include<bits/stdc++.h>
using namespace std;
int t,n,u[],v[],op[],tmp[],fa[];
int getfa(int x){
    return fa[x]==x?x:fa[x]=getfa(fa[x]);
}
void comb(int u,int v){
    int fu=getfa(u),fv=getfa(v);
    if(fu!=fv) fa[fu]=fv;
}
bool same(int u,int v){
    int fu=getfa(u),fv=getfa(v);
    return fu==fv;
}
int main(){
    scanf("%d",&t);
    while(t--){
        memset(u,,sizeof(u));
        memset(v,,sizeof(v));
        memset(op,,sizeof(op));
        memset(tmp,,sizeof(tmp));
        scanf("%d",&n);
        for(int i=;i<=*n;i++) fa[i]=i;
        for(int i=;i<=n;i++){
            scanf("%d%d%d",u+i,v+i,op+i);
            tmp[i*-]=u[i];
            tmp[i*]=v[i];
        }
        sort(tmp+,tmp+*n+);
        unique(tmp+,tmp+*n+);
        bool flag=true;
        for(int i=;i<=n;i++){
            u[i]=lower_bound(tmp+,tmp+*n+,u[i])-tmp;
            v[i]=lower_bound(tmp+,tmp+*n+,v[i])-tmp;
        }
        for(int i=;i<=n;i++)
            if(op[i]==) comb(u[i],v[i]);
        for(int i=;i<=n;i++)
            if(op[i]==)
                if(same(u[i],v[i])){
                    flag=false;break;
                }
        if(flag) printf("YES\n");
        else printf("NO\n");
    }
}

NOI2015D1T2

题目大意：一棵 $n$ 个点的树，点编号从 $0$ 到 $n-1$，$0$ 为根。一开始每个点点权均为 $0$。接下来有 $q$ 个操作：

• $\text{install}\ u$ 表示将 $u$ 到根的路径上的点点权都变为 $1$；
• $\text{uninstall}\ u$ 表示将 $u$ 子树中所有点点权都变为 $0$。

每次操作完后，询问有多少个点的点权在这次操作中发生了变化。

$1\le n,q\le 10^5$。

树剖裸题。时间复杂度 $O(n+q\log^2n)$。

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=;
struct edge{
    int to,nxt;
}e[maxn];
int n,q,el,dfn,head[maxn];
int dep[maxn],size[maxn],son[maxn],fa[maxn];
int id[maxn],w[maxn],top[maxn];
int sum[maxn<<],set[maxn<<];
inline void add(int u,int v){
    e[++el]=(edge){v,head[u]};
    head[u]=el;
}
void dfs1(int u,int f,int d){
    dep[u]=d;
    fa[u]=f;
    size[u]=;
    int maxson=-;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        dfs1(v,u,d+);
        size[u]+=size[v];
        if(size[v]>maxson){
            maxson=size[v];son[u]=v;
        }
    }
}
void dfs2(int u,int topf){
    id[u]=++dfn;
    top[u]=topf;
    if(!son[u]) return;
    dfs2(son[u],topf);
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==son[u]) continue;
        dfs2(v,v);
    }
}
inline void pushup(int t){
    sum[t]=sum[t<<]+sum[t<<|];
}
inline void pushdown(int l,int r,int t){
    if(~set[t]){
        int mid=l+r>>;
        set[t<<]=set[t];
        set[t<<|]=set[t];
        sum[t<<]=set[t]*(mid-l+);
        sum[t<<|]=set[t]*(r-mid);
        set[t]=-;
    }
}
void build(int l,int r,int t){
    if(l==r){
        set[t]=-;return;
    }
    int mid=l+r>>;
    build(l,mid,t<<);
    build(mid+,r,t<<|);
}
void setstate(int L,int R,int l,int r,int x,int t){
    if(L>=l && R<=r){
        set[t]=x;sum[t]=x*(R-L+);return;
    }
    pushdown(L,R,t);
    int mid=L+R>>;
    if(mid>=l) setstate(L,mid,l,r,x,t<<);
    if(mid<r) setstate(mid+,R,l,r,x,t<<|);
    pushup(t);
}
int getroot(){
    pushdown(,n,);
    return sum[];
}
int install(int u){
    int pre=getroot();
    while(u){
        setstate(,n,id[top[u]],id[u],,);
        u=fa[top[u]];
    }
    return getroot()-pre;
}
int uninstall(int u){
    int pre=getroot();
    setstate(,n,id[u],id[u]+size[u]-,,);
    return pre-getroot();
}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n-;i++){
        int x;
        scanf("%d",&x);
        add(x+,i+);
    }
    dfs1(,,);dfs2(,);
    build(,n,);
    scanf("%d",&q);
    for(int i=;i<=q;i++){
        char str[];int x;
        scanf("%s%d",str,&x);x++;
        if(str[]=='i') printf("%d\n",install(x));
        else printf("%d\n",uninstall(x));
    }
}

NOI2015D2T1

题目大意：有 $n$ 个字符串，第 $i$ 个在文章中出现了 $w_i$ 次。现在要把每个字符串替换成一个 $k$ 进制字符串（每个字符都是 $0$ 到 $k-1$ 的整数）。假设第 $i$ 个字符串被替换成了 $s_i$，那么要求对于任意 $i\ne j$ 都有 $s_i$ 不是 $s_j$ 的前缀。现在请求出替换后文章最小的长度（$\sum w_i|s_i|$），在此基础上求出 $\max(|s_i|)$ 的最小值。

$1\le n\le 10^5,2\le k\le 9,0\le w_i\le 10^{11}$。

实际上就是哈夫曼树的定义。那么求个 $k$ 进制哈夫曼树即可。

时间复杂度 $O(k+n\log n)$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=;
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline ll read(){
    char ch=getchar();ll x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int n,k;ll ans;
struct hhh{
    ll w;int h;
    bool operator<(const hhh &h)const{
        if(w!=h.w) return w>h.w;
        return this->h>h.h;
    }
};
priority_queue<hhh> pq;
int main(){
    n=read();k=read();
    FOR(i,,n) pq.push((hhh){read(),});
    if((n-)%(k-)!=) FOR(i,,k--(n-)%(k-)) pq.push((hhh){,});
    while(pq.size()!=){
        ll sum=;int hei=;
        FOR(i,,k){
            hhh h=pq.top();pq.pop();
            sum+=h.w;hei=max(hei,h.h);
        }
        pq.push((hhh){sum,hei+});ans+=sum;
    }
    printf("%lld\n%d\n",ans,pq.top().h-);
}

NOI2015D2T2

题目大意：有一个长度为 $n$ 的小写字母字符串 $s$，第 $i$ 个字符有权值 $a_i$。对于这个字符串的任意两个不同后缀 $p,q$，定义 $lcp(p,q)$ 为两个后缀的最长公共前缀的长度。现在对于每个 $0\le i\le n-1$，求出对于所有 $lcp(p,q)\ge i$ 的 $p,q$，$a_p\times a_q$ 的和和最大值。

$1\le n\le 3\times 10^5,|a_i|\le 10^9$。

之前没过的又臭又长又慢的做法的题解

（想看并查集做法的看别人的题解吧……）

NOI2016D1T1

题目大意：如果一个字符串可以被拆分为 $AABB$ 的形式，其中 $A$ 和 $B$ 是任意非空字符串，则我们称该字符串的这种拆分是优秀的。现在给出一个长度为 $n$ 的小写字母字符串 $S$，我们需要求出，在它所有子串的所有拆分方式中，优秀拆分的总个数。$T$ 组数据。

$1\le n\le 30000,1\le T\le 10$。

考虑计算以 $i$ 结尾的 $AA$ 有多少个（设为 $a_i$），以 $i$ 开头的 $AA$ 有多少个（设为 $b_i$），答案即为 $\sum a_ib_{i+1}$。

下面以求 $a_i$ 为例。枚举 $A$ 的长度 $l$，然后考虑 $l,2l,3l\dots\lfloor\frac{n}{l}\rfloor l$ 这些位置。

对于 $il$ 和 $(i+1)l$，求出这两个后缀的最长公共前缀和这两个前缀的最长公共后缀，设他们的长度分别为 $x$ 和 $y$。（与 $l$ 取最小值）

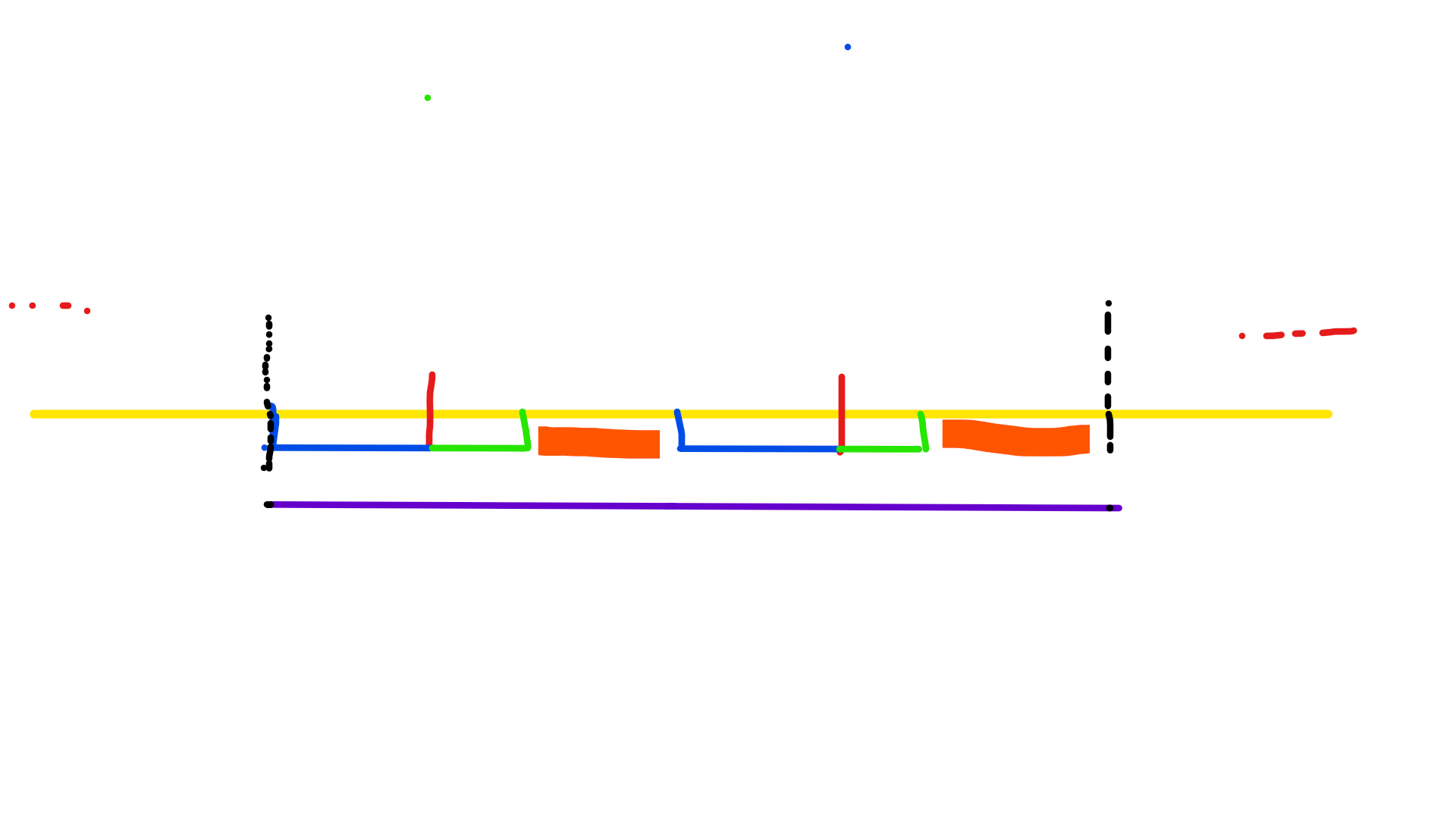
（从题解偷张图）

那么会发现，$x+y<l$ 时，红色荧光笔部分是无法匹配的，所以不存在满足要求的 $AA$ 串。

而当 $x+y\ge l$ 时：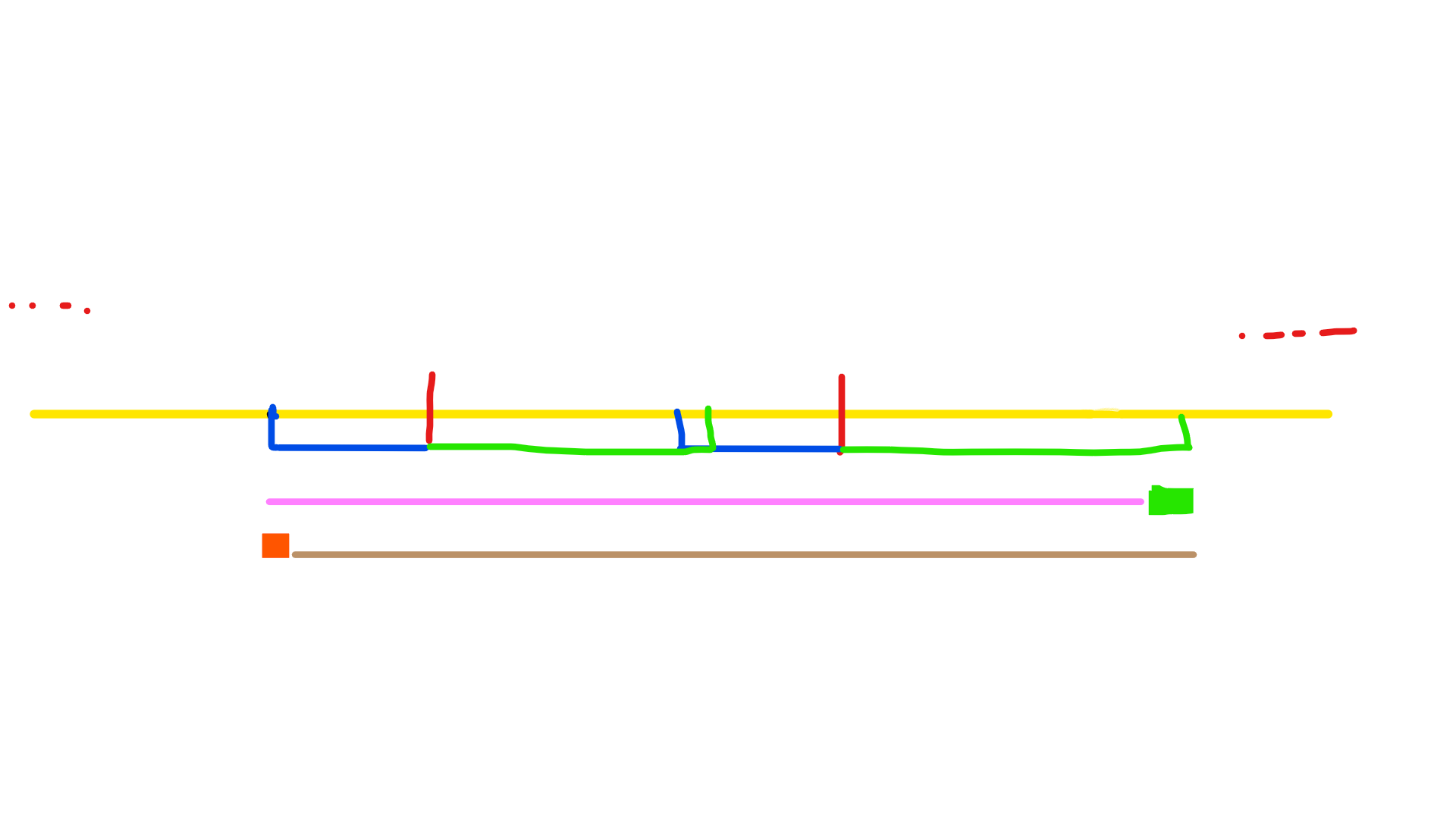

发现粉色和棕色的都是合法的 $AA$ 串。也就是说会对绿色荧光笔部分的每一个 $a$ 都产生 $1$ 的贡献。（这个区间是 $[(i+1)l-y+l-1,(i+1)l+x-1]$）

$b$ 同理。

求 $x,y$ 可以用后缀数组做到 $O(1)$，区间加可以用差分做到 $O(1)$。

总时间复杂度 $O(Tn\log n)$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=;
#define PB push_back
#define MP make_pair
#define lson o<<1,l,mid
#define rson o<<1|1,mid+1,r
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline int read(){
    char ch=getchar();int x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
struct Suffix_Array{
    char s[maxn];
    int n,m,cnt[maxn],sa[maxn],rak[maxn],tmp[maxn],h[maxn][],logt[maxn];
    void radix_sort(){
        MEM(cnt,);
        FOR(i,,n) cnt[rak[tmp[i]]]++;
        FOR(i,,m) cnt[i]+=cnt[i-];
        ROF(i,n,) sa[cnt[rak[tmp[i]]]--]=tmp[i];
    }
    void build(char s[]){
        MEM(sa,);MEM(rak,);MEM(tmp,);MEM(h,);
        n=strlen(s+);m=;
        FOR(i,,n) rak[tmp[i]=i]=s[i]-'a'+;
        radix_sort();
        for(int d=,p=;p<n;m=p,d<<=){
            p=;
            FOR(i,,d) tmp[++p]=n-d+i;
            FOR(i,,n) if(sa[i]>d) tmp[++p]=sa[i]-d;
            radix_sort();swap(rak,tmp);
            rak[sa[]]=p=;
            FOR(i,,n) rak[sa[i]]=(tmp[sa[i]]==tmp[sa[i-]] && tmp[sa[i]+d]==tmp[sa[i-]+d])?p:++p;
        }
        int k=;
        FOR(i,,n){
            if(k) k--;
            for(int j=sa[rak[i]-];s[i+k]==s[j+k];k++);
            h[rak[i]][]=k;
        }
        logt[]=;FOR(i,,n) logt[i]=logt[i>>]+;
        FOR(j,,logt[n]+) FOR(i,,n-(<<j)+) h[i][j]=min(h[i][j-],h[i+(<<j-)][j-]);
    }
    int LCP(int x,int y){
        x=rak[x];y=rak[y];
        if(x>y) swap(x,y);
        x++;
        int k=logt[y-x+];
        return min(h[x][k],h[y-(<<k)+][k]);
    }
}nor,rev;
int n;
char str[maxn];
ll ans,a[maxn],b[maxn];
int main(){
    for(int t=read();t;t--){
        scanf("%s",str+);n=strlen(str+);
        nor.build(str);
        for(int i=,j=n;i<j;i++,j--) swap(str[i],str[j]);
        rev.build(str);
        MEM(a,);MEM(b,);ans=;
        FOR(l,,n/){
            for(int i=l,j=l<<;j<=n;i+=l,j+=l){
                int x=min(l,nor.LCP(i,j)),y=min(l-,rev.LCP(n-i+,n-j+));
                if(x+y>=l){
                    a[j+x-(x+y-l+)]++;a[j+x]--;
                    b[i-y+(x+y-l+)]--;b[i-y]++;
                }
            }
        }
        FOR(i,,n) a[i]+=a[i-],b[i]+=b[i-];
        FOR(i,,n-) ans+=a[i]*b[i+];
        printf("%lld\n",ans);
    }
}

NOI2016D2T1

题目大意：有 $n$ 个区间 $[l_i,r_i]$。现在你要选出 $m$ 个区间，使得至少有一个整点被所有的这些区间覆盖到。对于一个选取方案价值是所有区间的最大长度与最小长度的差。问最小价值。如果没有合法选取方案输出 $-1$。

$1\le n\le 5\times 10^5,1\le m\le 2\times 10^5,0\le l_i\le r_i\le 10^9$。

首先把区间按长度从小到大排序。枚举最短的区间，然后找最长的区间，使得至少有一个点被覆盖至少 $m$ 次（然后就能从里面选出这 $m$ 个区间，是符合要求的）。想让价值最小，就是找到最前面的最长区间。发现这个区间不降，所以可以尺取法。

至少一个点覆盖 $m$ 次，还有区间加操作，可以变成求区间最大值的线段树。注意在线段树上操作最好先离散化。

时间复杂度 $O(n\log n)$。

#include<bits/stdc++.h>
using namespace std;
const int maxn=,maxm=;
int n,m,sz,tmp[maxn*];
int cnt,rt,mx[maxn*],add[maxn*],ch[maxn*][];
struct interval{
    int l,r,len;
    bool operator<(const interval &i)const{return len<i.len;}
}seg[maxn];
inline int binary(int x){return lower_bound(tmp+,tmp+sz+,x)-tmp;}
inline void pushup(int x){mx[x]=max(mx[ch[x][]],mx[ch[x][]]);}
inline void pushdown(int x){
    if(add[x]){
        add[ch[x][]]+=add[x];add[ch[x][]]+=add[x];
        mx[ch[x][]]+=add[x];mx[ch[x][]]+=add[x];
        add[x]=;
    }
}
void build(int &x,int l,int r){
    x=++cnt;if(l==r) return;
    int mid=(l+r)>>;
    build(ch[x][],l,mid);build(ch[x][],mid+,r);
}
void update(int x,int l,int r,int ql,int qr,int v){
    if(l>=ql && r<=qr) return void((add[x]+=v,mx[x]+=v));
    int mid=(l+r)>>;
    pushdown(x);
    if(mid>=ql) update(ch[x][],l,mid,ql,qr,v);
    if(mid<qr) update(ch[x][],mid+,r,ql,qr,v);
    pushup(x);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++){
        scanf("%d%d",tmp+i*-,tmp+i*);
        seg[i]=(interval){tmp[i*-],tmp[i*],tmp[i*]-tmp[i*-]};
    }
    sort(tmp+,tmp+*n+);sort(seg+,seg+n+);
    build(rt,,sz=unique(tmp+,tmp+*n+)-tmp-);
    for(int i=;i<=n;i++) seg[i].l=binary(seg[i].l),seg[i].r=binary(seg[i].r);
    int cl=,ans=INT_MAX;
    for(int i=;i<=n;i++){
        update(rt,,sz,seg[i].l,seg[i].r,);
        while(cl<=i && mx[rt]>=m){
            ans=min(ans,seg[i].len-seg[cl].len);
            update(rt,,sz,seg[cl].l,seg[cl].r,-);
            cl++;
        }
    }
    printf("%d\n",ans==INT_MAX?-:ans);
}

NOI2017D1T1

题目大意：有一个大整数 $x$，一开始是 $0$。一共有 $n$ 个操作，有两种操作：

• $1\ a\ b$ 表示将 $x$ 加上 $a\times 2^b$
• $2\ k$ 表示询问 $x$ 的二进制表示下的第 $k$ 位

$1\le n\le 10^6,|a|\le 10^9,0\le b,k\le 3\times 10^7$，任意时刻 $x\ge 0$。

先考虑修改操作。

有一个结论：如果每次都加正数（以下把加正数叫加，加负数叫减），那么每次暴力进位复杂度均摊 $O(1)$。

然而这是只有加操作，再有减操作时，就不能暴力进退位了。

那么可以考虑记录两个数（记为 $add$ 和 $sub$），分别表示加了多少和减了多少，目前每一次操作均摊 $O(1)$。

再考虑询问操作。

发现当有一位发生退位时，那么从这位的高一位开始，一整段连续的 $0$（也就是这些位上 $add$ 都和 $sub$ 相等）都会变成 $1$，这段后的 $1$ 会变成 $0$。

所以对于一位 $k$，从这一位的低一位开始，找到第一位 $add\ne sub$ 的位置，如果这一位上 $add>sub$（不借位），那么第 $k$ 位不会变，否则第 $k$ 位会变。

问题变为比较两个超多位数的数的大小。

可以维护所有 $add\ne sub$ 的位（用 set 存），然后求出比 $k$ 低的第一位不同的位，比较即可。

修改时可以简单修改一下这个 set。

时间复杂度 $O(n\log n)$。

下面的代码压了 $30$ 位。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=;
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline int read(){
    int x=,f=;char ch=getchar();
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int n;
ll add[maxn],sub[maxn];
set<int,greater<int> > s;
int main(){
    n=read();read();read();read();
    while(n--){
        int op=read(),x=read(),y;
        if(op==){
            y=read();
            int a=y/,b=y%,cnt=;
            if(x>){
                add[a]+=(ll)x<<b;
                while(add[a]>> || cnt<=){
                    if(!(add[a]>>)) cnt++;
                    add[a+]+=add[a]>>;
                    add[a]&=(<<)-;
                    if(add[a]!=sub[a]) s.insert(a);
                    else if(s.count(a)) s.erase(a);
                    a++;
                }
            }
            else if(x<){
                sub[a]+=(ll)(-x)<<b;
                while(sub[a]>> || cnt<=){
                    if(!(sub[a]>>)) cnt++;
                    sub[a+]+=sub[a]>>;
                    sub[a]&=(<<)-;
                    if(add[a]!=sub[a]) s.insert(a);
                    else if(s.count(a)) s.erase(a);
                    a++;
                }
            }
        }
        else{
            int a=x/,b=x%,t1=add[a]&((<<b)-),t2=sub[a]&((<<b)-),t=((add[a]^sub[a])>>b)&;
            set<int,greater<int> >::iterator it=s.lower_bound(a-);
            if(t1>t2 || t1==t2 && (it==s.end() || add[*it]>sub[*it])) printf("%d\n",t);
            else printf("%d\n",t^);
        }
    }
}

NOI2017D2T1

题目大意：有一个长度为 $n$ 的字符串 $S$，只包含 $\text{a,b,c,x}$。现在你要把每个字符都替换成 $\text{A,B,C}$ 中的一个，其中 $\text{a}$ 不能替换成 $\text{A}$，$\text{b}$ 不能替换成 $\text{B}$，$\text{c}$ 不能替换成 $\text{C}$，$\text{x}$ 任意。另外有 $m$ 个限制 $p_1,c_1,p_2,c_2$，表示如果第 $p_1$ 个字母被替换成了 $c_1$，那么第 $p_2$ 个字母就一定要被替换成 $c_2$。请求出一种合法方案。如果无解输出 $-1$。

$1\le n\le 50000,0\le m\le 100000$，$\text{x}$ 的个数（称为 $d$） $\le 8$。

先考虑没有 $d=0$ 怎么做。发现是 2-SAT 裸题。

然后可以枚举把每个 $\text{x}$ 看成是 $\text{a}$ 还是 $\text{b}$ 还是 $\text{c}$。所有的合法情况一定都被枚举到了。

时间复杂度 $O(3^d(n+m))$，不能通过。

发现只需要枚举 $\text{a}$ 和 $\text{b}$ 就够了，也已经把选 $\text{A,B,C}$ 的情况都考虑到了。

时间复杂度 $O(2^d(n+m))$。

#include<bits/stdc++.h>
using namespace std;
const int maxn=;
#define MP make_pair
#define PB push_back
#define lson o<<1,l,mid
#define rson o<<1|1,mid+1,r
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline int read(){
    char ch=getchar();int x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int n,d,m,c,ai[maxn*],bi[maxn*],id[maxn];
int stk[maxn*],tp,scnt,scc[maxn*],dfn[maxn*],low[maxn*],dcnt;
int el,head[maxn*],to[maxn*],nxt[maxn*];
char s[maxn],hai[maxn*],hbi[maxn*];
bool nota[],vis[maxn*];
inline void add(int u,int v){
    to[++el]=v;nxt[el]=head[u];head[u]=el;
}
void tarjan(int u){
    dfn[u]=low[u]=++dcnt;
    vis[stk[++tp]=u]=true;
    for(int i=head[u];i;i=nxt[i]){
        int v=to[i];
        if(!dfn[v]) tarjan(v),low[u]=min(low[u],low[v]);
        else if(vis[v]) low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u]){
        scnt++;
        do{
            scc[stk[tp]]=scnt;
            vis[stk[tp]]=false;
        }while(stk[tp--]!=u);
    }
}
inline int type(char a,char b){
    return a=='a' && b=='c' || a=='b' && b=='c' || a=='c' && b=='b';
}
void SAT_2(){
    tp=scnt=dcnt=el=;MEM(stk,);MEM(scc,);MEM(dfn,);MEM(low,);MEM(head,);MEM(to,);MEM(nxt,);
    FOR(i,,n) if(id[i]) s[i]=nota[id[i]]?'a':'b';
    FOR(i,,m){
        if(s[ai[i]]==hai[i]) continue;
        if(s[bi[i]]==hbi[i]) add(*ai[i]+type(s[ai[i]],hai[i]),*ai[i]+!type(s[ai[i]],hai[i]));
        else add(*ai[i]+type(s[ai[i]],hai[i]),*bi[i]+type(s[bi[i]],hbi[i])),add(*bi[i]+!type(s[bi[i]],hbi[i]),*ai[i]+!type(s[ai[i]],hai[i]));
    }
    FOR(i,,*n+) if(!dfn[i]) tarjan(i);
    FOR(i,,n) if(scc[*i]==scc[*i+]) return;
    FOR(i,,n){
        if(s[i]=='a') putchar(scc[*i]<scc[*i+]?'B':'C');
        if(s[i]=='b') putchar(scc[*i]<scc[*i+]?'A':'C');
        if(s[i]=='c') putchar(scc[*i]<scc[*i+]?'A':'B');
    }
    exit();
}
void dfs(int dep){
    if(dep>d) return SAT_2();
    dfs(dep+);
    nota[dep]=true;
    dfs(dep+);
    nota[dep]=false;
}
int main(){
    n=read();d=read();
    scanf("%s",s+);
    FOR(i,,n) if(s[i]=='x') id[i]=++c;
    m=read();
    FOR(i,,m){
        ai[i]=read();
        while(hai[i]<'A' || hai[i]>'C') hai[i]=getchar();hai[i]+='a'-'A';
        bi[i]=read();
        while(hbi[i]<'A' || hbi[i]>'C') hbi[i]=getchar();hbi[i]+='a'-'A';
    }
    dfs();
    printf("-1");
}

NOI2018D1T1

题目大意：$T$ 组数据。给一个 $n$ 个点 $m$ 条边的无向连通图，每条边有长度 $l_i$ 和权值 $a_i$。$q$ 次询问，每次给定起点 $u$ 和权值下限 $x$，问对于所有能只经过 $a_i>x$ 的边就走到 $u$ 的点，到 $1$ 的最短路的最小值。强制在线。

$1\le T\le 3,1\le n\le 2\times 10^5,0\le m,q\le 4\times 10^5$。

首先预处理每个点到 $1$ 的最短路。

将边按 $a_i$ 从大到小排序，然后建出 kruskal 重构树，那么 $u$ （新点，代表原来的边）的子树中就是可以只经过超过 $a_u$ 的边互达的点。每次询问时，从点 $u$（原点）倍增，跳到第一个父亲的 $a\le x$ 的位置，答案就是这棵子树中最短路的最小值。

时间复杂度 $O(T(m\log n+m\log m+q\log n))$。

#include<bits/stdc++.h>
using namespace std;
#define mem(x) (memset(x,0,sizeof(x)))
typedef long long ll;
const int maxn=,maxm=;
struct edge1{
    int u,v,w;
    bool operator<(const edge1 e)const{
        return w>e.w;
    }
}e1[maxm];
struct edge2{
    int v,w,nxt;
}e2[maxm<<],e3[maxn<<];
struct state{
    int u;ll dis;
    bool operator<(const state s)const{
        return dis>s.dis;
    }
};
int t,n,m,q,k,s,lastans;
int el2,el3,head2[maxn],head3[maxn<<];
int u_fa[maxn<<],cnt;
ll dis[maxn],w[maxn<<],mind[maxn<<],fa[maxn<<][];
priority_queue<state> pq;
inline void add2(int u,int v,int w){
    e2[++el2]=(edge2){v,w,head2[u]};head2[u]=el2;
}
inline void add3(int u,int v){
    e3[++el3]=(edge2){v,,head3[u]};head3[u]=el3;
}
void dijkstra(){
    while(!pq.empty()) pq.pop();
    memset(dis,0x3f,sizeof(dis));
    dis[]=;
    pq.push((state){,});
    while(!pq.empty()){
        int u=pq.top().u;ll d=pq.top().dis;pq.pop();
        if(d>dis[u]) continue;
        for(int i=head2[u];i;i=e2[i].nxt){
            int v=e2[i].v;
            if(dis[u]+e2[i].w<dis[v]) pq.push((state){v,dis[v]=dis[u]+e2[i].w});
        }
    }
}
int getfa(int x){
    return x==u_fa[x]?x:u_fa[x]=getfa(u_fa[x]);
}
void kruskal(){
    sort(e1+,e1+m+);
    for(int i=;i<=n*-;i++) u_fa[i]=i;
    for(int i=;i<=n;i++) w[i]=-1e18;
    cnt=n;
    for(int i=;i<=m;i++){
        int u=e1[i].u,v=e1[i].v;
        u=getfa(u);v=getfa(v);
        if(u==v) continue;
        w[++cnt]=e1[i].w;
        u_fa[u]=u_fa[v]=cnt;
        add3(cnt,u);add3(cnt,v);
    }
}
void dfs(int u){
    mind[u]=u>n?1e18:dis[u];
    for(int i=;i<=;i++) fa[u][i]=fa[fa[u][i-]][i-];
    for(int i=head3[u];i;i=e3[i].nxt){
        int v=e3[i].v;
        fa[v][]=u;
        dfs(v);
        mind[u]=min(mind[u],mind[v]);
    }
}
ll calc(ll st,ll p){
    for(int i=;~i;i--)
        if(w[fa[st][i]]>p) st=fa[st][i];
    return mind[st];
}
int main(){
    scanf("%d",&t);
    while(t--){
        mem(e1);mem(e2);mem(e3);mem(head2);mem(head3);mem(w);mem(mind);mem(fa);
        w[lastans=el2=el3=cnt=]=-1e18;
        scanf("%d%d",&n,&m);
        for(int i=;i<=m;i++){
            int u,v,w1,w2;
            scanf("%d%d%d%d",&u,&v,&w1,&w2);
            e1[i]=(edge1){u,v,w2};
            add2(u,v,w1);add2(v,u,w1);
        }
        dijkstra();
        kruskal();
        fa[cnt][]=;
        dfs(cnt);
        scanf("%d%d%d",&q,&k,&s);
        for(int i=;i<=q;i++){
            int st,p;
            scanf("%d%d",&st,&p);
            st=(st+k*lastans-)%n+;
            p=(p+k*lastans)%(s+);
            printf("%lld\n",lastans=calc(st,p));
        }
    }
}

NOI2018D2T1

之前写过。