数据结构与算法17—B树(B、B+、B*)

B树

B-树，就是B树，B树的原英文名是B-tree,所以很多翻译为B-树,就会很多人误以为B-树是一种树、B树是另外一种树。其实，B-tree就是B树。

B-树的定义

B树（B-tree）是一种树状数据结构，是一种平衡的多路查找树，能够用来存储排序后的数据。这种数据结构能够让查找数据、循序存取、插入数据及删除的动作，都在对数时间内完成。B树，概括来说是一个一般化的二叉查找树，可以拥有多于2个子节点。与自平衡二叉查找树不同，B-树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程，从而加快存取速度。这种数据结构常被应用在数据库和文件系统的实作上。

一棵m阶的B-树,或为空树,或为满足下列特性的m叉树:

(1)树中每个结点至多有m棵子树(m>=2)。

(2)除非根结点为叶子结点,否则至少有两棵子树。

(3)除根之外的所有非终端结点至少有┌m/2┐棵子树。

(4)每个结点存放至少m/2-1（取上整）和至多m-1个关键字；(至少2个关键字）

(5)非叶子结点的关键字个数=指向儿子的指针个数-1；

(6)所有的非终端结点的结构如下:

其中,k1,k2,...,kn为n个按从小到大顺序排列的键值;

(7)所有叶子结点在同一个层次上,且不含有任何信息。

下图是一棵四阶(m=5)B_树的示意图,该树共有四层,所有叶子点均在第四层上。这里为了理解方便我就直接用实际字母的大小来排列C>B>A）(注：通常树结点的首位置要存储此结点的有效数据个数)

 

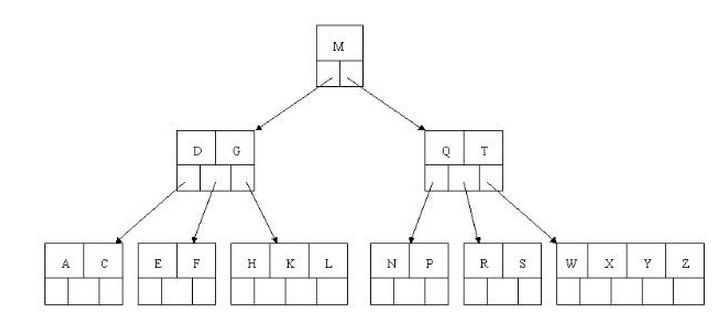
B树的查询流程

如上图我要从上图中找到E字母，查找流程如下

（1）获取根节点的关键字进行比较，当前根节点关键字为M，E<M（26个字母顺序），所以往找到指向左边的子节点（二分法规则，左小右大，左边放小于当前节点值的子节点、右边放大于当前节点值的子节点）；

（2）拿到关键字D和G，D<E<G 所以直接找到D和G中间的节点；

（3）拿到E和F，因为E=E 所以直接返回关键字和指针信息（如果树结构里面没有包含所要查找的节点则返回null）；

B树的插入(建立)节点

关键字插入的位置必定在最下 层的非叶结点，有下列几种情况：

1）插入后，该结点的关键字个数n<m， 不修改指针;

2）插入后，该结点的关键字个数 n=m， 则需进行“结点分裂”，令 s =┌m/2┐， 在原结点中保留 （A0，K1，…… ， K_s-1，A_s-1）； 建新结点 （A_s，K_s+1，…… ，K_n，A_n）； 将（K_s，p）插入双亲结点；

3）若双亲为空，则建新的根结点。

例如：定义一个5阶树（平衡5路查找树），现在要把3、8、31、11、23、29、50、28 这些数字构建出一个5阶树出来

a. 先插入 3、8、31、11

b.再插入23、29

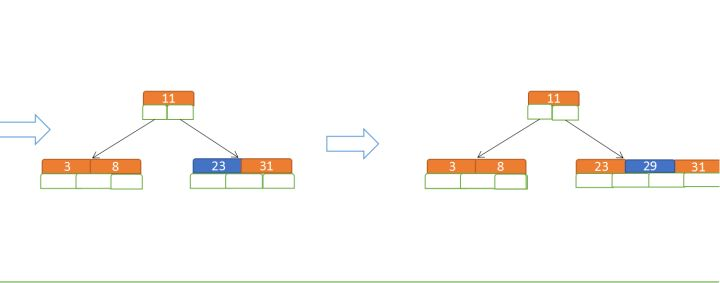
插入23时，m=5了，而因5阶树关键字数必<=5-1，所以在┌m/2┐处拆分。

c.再插入50、28

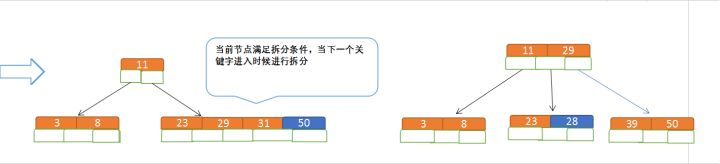
同理，插入50时，m<5，所以不用改变。而插入28时与b步骤相同。

B树节点的删除

(1) 在深度为(h+l)的m阶B-树中删除一个键值k,首先要查到键值k所在的结点及在结点中的位置。若k在非终端节点中，则把该结点的右边(或左边)指针所指子树中的最小(或最大)键值与k对调，使k移到终端节点。

(2) 在终端节点中删除一个键值后,使得该结点的值个数n减1,此时应分以下三种情况进行处理：

a. 若删除后结点中键值数目n≥ ┌m/2┐－1,在该结点中删去键值k连同右边的指针。

b. 若删除后结点中键值数目n< ┌m/2┐－1,且左(或右)兄弟结点的关键字数目＞ ┌m/2┐－1,则把左(或右)兄弟结点中最大(或最小)键值移到父结点中,再把父结点大于(或小于)上移键值的键值下移到被删关键字所在结点中。

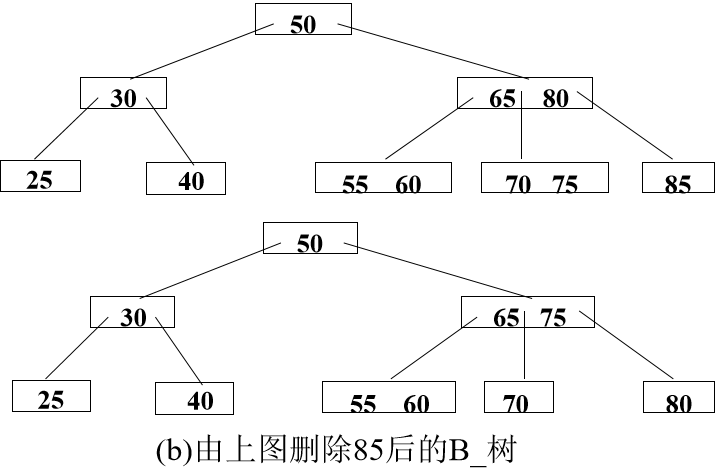
c. 若删除后结点中键值数目n< ┌m/2┐－1,及其左、右兄弟结点的键值数目都等于┌m/2┐－1,则就必须进行结点的“合并”,即把应删的键值删去后,将该结点中的剩余键值和指针连同父结点中指向该结点指针的左边(或右边)一个键值ki一起合并到左兄弟(或右兄弟)结点中,将ki从父结点中删去。如果因此使父结点中关键字数目< ┌m/2┐－1,则对此父结点做同样处理,以致于可能直到对根结点做这样的处理而使整个树减少一层。

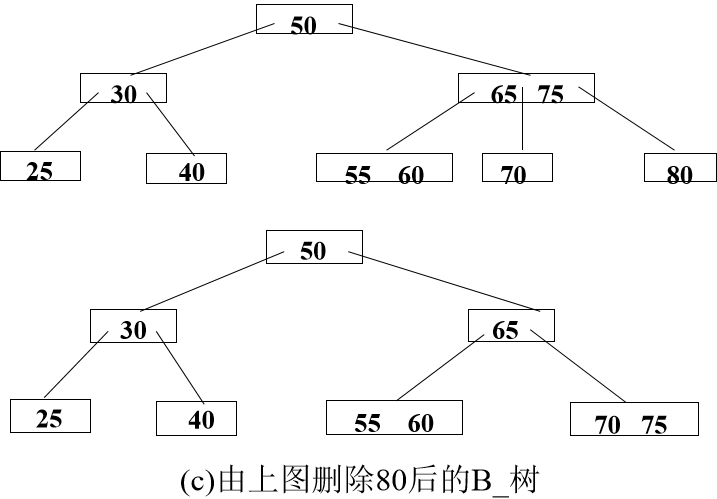
如果因此使父结点中关键字数目< ┌m/2┐－1,则对此父结点做同样处理,以致于可能直到对根结点做这样的处理而使整个树减少一层。

B树特点：

B树相对于平衡二叉树的不同是，每个节点包含的关键字增多了，特别是在B树应用到数据库中的时候，数据库充分利用了磁盘块的原理（磁盘数据存储是采用块的形式存储的，每个块的大小为4K，每次IO进行数据读取时，同一个磁盘块的数据可以一次性读取出来）把节点大小限制和充分使用在磁盘快大小范围；把树的节点关键字增多后树的层级比原来的二叉树少了，减少数据查找的次数和复杂度;

B+树

B+树是B树的一个升级版，相对于B树来说B+树更充分的利用了节点的空间，让查询速度更加稳定，其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定；我们先看看两者的区别。

B+树是B树的变体，也是一种多路搜索树，其定义基本与B-树相同，除了：

• 1）非叶子结点的子树指针与关键字个数相同；
• 2）非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；
• 3）为所有叶子结点增加一个链指针；
• 4）所有关键字都在叶子结点出现；

B+树的搜索与B树也基本相同，区别是B+树只有达到叶子结点才命中（B树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

B+树的性质：

• 1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
• 2.不可能在非叶子结点命中；
• 3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
• 4.更适合文件索引系统。

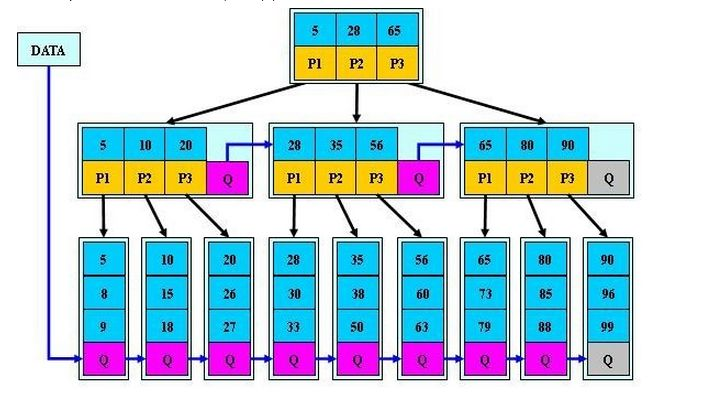
如（m=3）：

B+树比B树更适合操作系统的文件索引和数据库索引的原因：

• B+树的磁盘读写代价更低，B+树的内部节点没有指向关键字具体信息的指针，因此内部节点相对B树更小。如果把所有同一内部节点的关键字放在同一块磁盘中，盘块所能容纳的关键字数量也就越多，一次性读入内存中的需要查找的关键字也就越多，相对IO读写次数降低。
• B+树的查询效率更加稳定
  由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

所以，B+树只要遍历叶子节点就可以实现整棵树的遍历，支持基于范围的查询，而B树不支持range-query这样的操作（或者说效率太低）。

B*树

B∗树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针，将结点的最低利用率从1/2提高到2/3。

B∗树定义了非叶子结点关键字个数至少为2/3M，即块的最低使用率为2/3（代替B+树的1/2）；

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

B∗树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

所以，B∗树分配新结点的概率比B+树要低，空间使用率更高。

特点

在B+树的基础上因其初始化的容量变大，使得节点空间使用率更高，而又存有兄弟节点的指针，可以向兄弟节点转移关键字的特性使得B*树额分解次数变得更少；

参考：

1、https://zhuanlan.zhihu.com/p/27700617

2、https://blog.csdn.net/v_JULY_v/article/details/6530142/

3、https://blog.csdn.net/endlu/article/details/51720299

4、https://www.cnblogs.com/nullzx/p/8729425.html