【牛客】小w的魔术扑克（并查集？？树状数组）

题目描述

小w喜欢打牌，某天小w与dogenya在一起玩扑克牌，这种扑克牌的面值都在1到n，原本扑克牌只有一面，而小w手中的扑克牌是双面的魔术扑克（正反两面均有数字，可以随时进行切换），小w这个人就准备用它来出老千作弊。小w想要打出一些顺子，我们定义打出一个l到r的顺子需要面值为从l到r的卡牌各一张。小w想问问你，他能否利用手中的魔术卡牌打出这些顺子呢？

输入描述:

首先输入一行2个正整数n，k，表示牌面为1~n，小w手中有k张魔术扑克牌。
然后输入k行，每行两个数字，表示卡牌的正面和反面的面值。
接下来输入一行一个正整数q，表示q组查询，然后每组占一行查询输入两个整数l,r。表示查询小w能否打出这么一个l到r的顺子。

输出描述:

对于输出"Yes"表示可以，"No"表示不可以。（不含引号）
每个查询都是独立的，查询之间互不影响。
示例1
输入
5 3
1 2
2 3
4 4
3
1 2
2 4
1 4
输出
Yes
Yes
No
说明
对于顺子1~2，可以选择第一张卡牌作为'1'使用，选择第二张卡牌作为'2'使用。
对于顺子2~4，可以选择第一张卡牌作为'2'使用，选择第二张卡牌作为'3'使用，选择第三张卡牌作为'4'使用。
对于顺子1~4，由于牌的数目都不够，显然无法打出。
示例2
输入
4 3
1 1
2 2
4 4
3
1 2
1 4
4 4
输出
Yes
No
Yes

分析

一开始想用dp，贪心，二分图之类的始终没想出来，后来强行逼自己往图论方面想才想到了解法

对于任意一张卡片我们可以把它看成一条边，将两个值连起来，而选择哪个值相当于给这条边定向

就拿样例1举例子，样例1的图如下

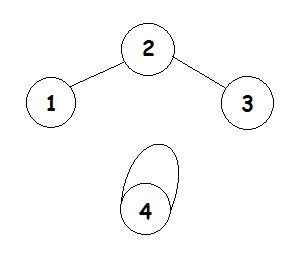
每张牌选哪个值，对应的那条边就指向哪个值

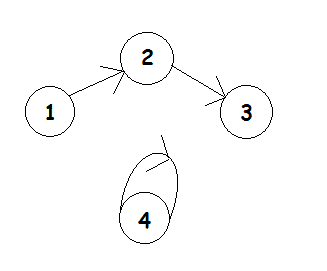
比如现在我们要凑出顺子[2,4]，显然1不在顺子里，2在顺子里，那么连接1,2的边肯定指向2

那么结果如图

进而我们得出一个结论，在同一个联通块里面的数值，假设连通块大小为n，如果这个连通块是一棵树，那么连通块里面最多能取n-1个点（只有n-1条边）。

而且我们可以决定这n-1个点分别是哪些（只要找到不取的点，将它周围的边都指向其它节点，依次推下去即可

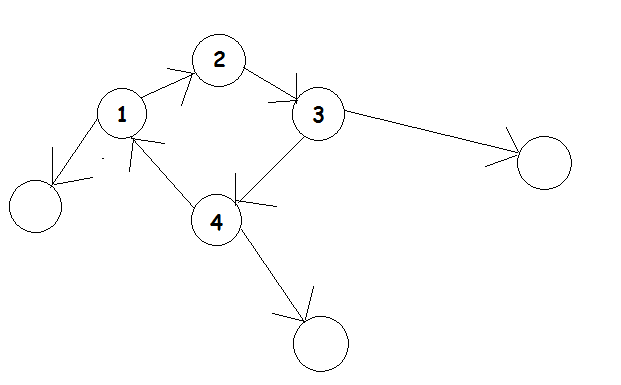
如果这个联通块中存在环，那么这个连通块中的所有点都可以取，如图

那么对于每棵树，我们求出它最小节点和最大节点，如果询问区间同时包含了最小节点和最大节点，就相当于包含了这棵树，

这个时候因为肯定有1个点取不到，所以肯定完成不了

所以对于每棵树求出它的最小节点，最大节点，这两个节点形成一段区间，包含这段区间的询问区间就无法完成

接下来就相当于要判断询问区间是否包含这些区间

如果一段区间[l,r]包含另一端区间[l1,r1]，那么一定满足l<l1且r1<r。

在l1位置插入值r1，在l位置查询后缀最小值，如果该值小于r,那么一定存在左端点在l后面，右端点在r左边的区间，即被包含的区间

这个可以用数组维护，也可以O（n）扫过去预处理。

Code

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
int n,k,Q,mn[maxn],mx[maxn],bit[maxn],ori[maxn],vis[maxn],cnt[maxn][];
int find(int x){return !ori[x]?x:ori[x]=find(ori[x]);}
void add(int x,int k){for(;x;x-=(x&-x))bit[x]=min(bit[x],k);}
int que(int x){int ret=bit[];for(;x<=n;x+=(x&-x))ret=min(ret,bit[x]);return ret;}
int main()
{
    scanf("%d%d",&n,&k);for(int i=;i<=n;i++)cnt[i][]=;
    for(int i=,s1,s2;i<=k;i++)
    {
        scanf("%d%d",&s1,&s2);
        s1=find(s1);s2=find(s2);
        if(s1==s2){cnt[s1=s2][]++;continue;}
        cnt[s1][]+=cnt[s2][];cnt[s1][]+=cnt[s2][]+;ori[s2]=s1;
    }
    for(int i=,s;i<=n;i++)if(!vis[s=find(i)])vis[s]=,mx[s]=i,mn[s]=i;else mx[s]=i;
    memset(vis,,sizeof vis);memset(bit,0x3f,sizeof bit);
    for(int i=,s;i<=n;i++)if(!vis[s=find(i)]){vis[s]=;if(cnt[s][]>cnt[s][])add(mn[s],mx[s]);}
    scanf("%d",&Q);
    for(int i=,l,r;i<=Q;i++)
    {
        scanf("%d%d",&l,&r);
        if(r>=que(l))puts("No");else puts("Yes");
    }
}