（十三）GBDT模型用于评分卡模型python实现

python信用评分卡建模（附代码，博主录制）

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

GBDT模型用于评分卡模型

https://blog.csdn.net/LuYi_WeiLin/article/details/88397303 转载
本文主要总结以下内容：

GBDT模型基本理论介绍
GBDT模型如何调参数
GBDT模型对样本违约概率进行估计（GBDT模型用于评分卡python代码实现请看下一篇博客）
GBDT模型挑选变量重要性
GBDT模型如何进行变量的衍生

GBDT模型基本理论介绍
GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。GBDT中的树是回归树（不是分类树），GBDT用来做回归预测，调整后也可以用于分类。

GBDT模型是集成学习框架Boosting的一种

一句话解释版本：

Bagging是决策树的改进版本，通过拟合很多决策树来实现降低方差

随机森林（Random Forrest）是Bagging的改进版本，通过限制节点可选特征范围优化Bagging

Boosting是Bagging的改进版本，通过吸取之前树的经验建立后续树优化Bagging

Boosting模型工作原理

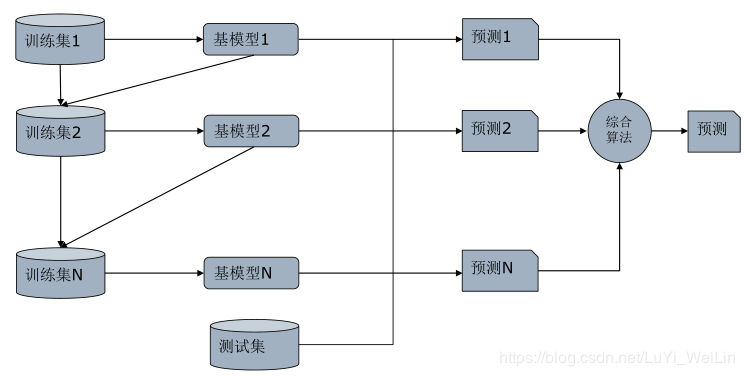
• GBDT模型的原理

Y标签类别可以是（连续型[基模型：回归]、离散无序型[基模型：分类]、离散有序型[基模型：排序]）

不同的Y标签类型选择不一样的损失函数，上式中损失函数L(F(X),Y),其中Y是固定的，F(X)的针对不同问题，函数结构也是可以定下来的，唯一要确定的是函数所对应的参数使得该损失函数最小，所以我们把问题从函数空间搜索问题转换为参数空间搜索问题

常见的损失函数（针对不同Y标签类型选择不一样的损失函数）
Y标签类别可以是（连续型[基模型：回归]、离散无序型[基模型：分类]、离散有序型[基模型：排序]）

下面三个分别对应：回归型损失函数、分类型损失函数、逻辑回归损失函数（当然了这里只是举了常见的三个，比如回归型损失函数我们也可以使用均方差等损失函数，这里不过多去展开）

针对GBDT模型我们如何寻找最优参数呢？

运用最优化的思想，采用迭代的方法求出其参数（因为现实中是很难求其精确解的，就算可以求解也要花费大量的时间，我们可以问题简化，求出P的近似解即可，无限的逼近到一个我们可以接受的范围即可），如何迭代呢？我们先了解一下梯度法

• 梯度法

梯度提升法

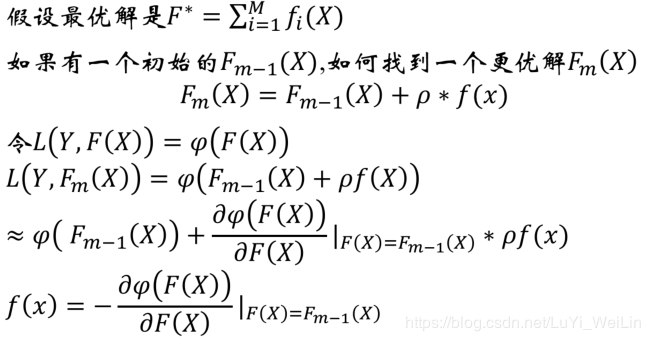
可能看到这里有的小伙伴已经云里雾里了，说的是什么呢？不急我们先来引用一下别人的例子（https://blog.csdn.net/zhangbaoanhadoop/article/details/81840669文章不错，建议大家去看一下）

---------------------------------------------------------------------------------------------------------------------------------------------------------------------

让损失函数沿着梯度方向的下降。这个就是gbdt 的 gb的核心。gbdt 每轮迭代的时候，都去拟合损失函数在当前模型下的负梯度。（如果损失函数使用的是平方误差损失函数，则这个损失函数的负梯度就可以用残差来代替，以下所说的残差拟合，便是使用了平方误差损失函数）

Boosting，迭代，即通过迭代多棵树来共同决策。这怎么实现呢？难道是每棵树独立训练一遍，比如A这个人，第一棵树认为是10岁，第二棵树认为是0岁，第三棵树认为是20岁，我们就取平均值10岁做最终结论？--当然不是！且不说这是投票方法并不是GBDT，只要训练集不变，独立训练三次的三棵树必定完全相同，这样做完全没有意义。之前说过，GBDT是把所有树的结论累加起来做最终结论的，所以可以想到每棵树的结论并不是年龄本身，而是年龄的一个累加量。GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。

还是年龄预测，简单起见训练集只有4个人，A,B,C,D，他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生；C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练，会得到如下图2所示结果：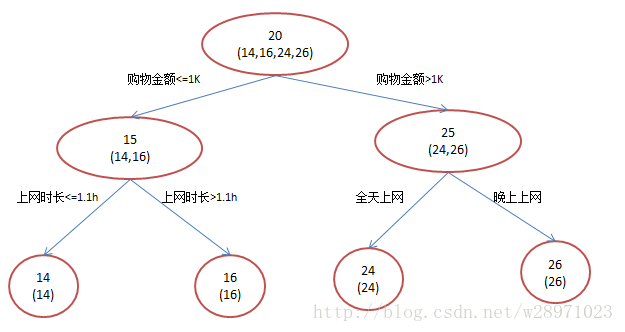

图2：传统回归决策树

现在我们使用GBDT来做这件事，由于数据太少，我们限定叶子节点做多有两个，即每棵树都只有一个分枝，并且限定只学两棵树。我们会得到如下图3所示结果：

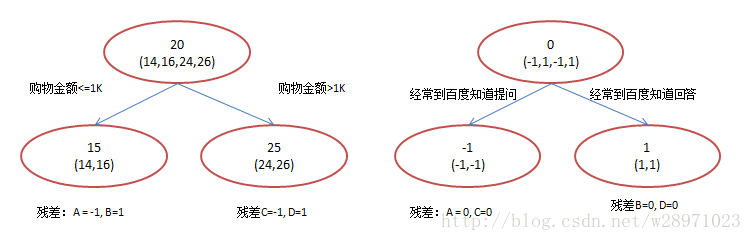
图3：GBDT模型

在第一棵树分枝和图2一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。此时计算残差（残差的意思就是： A的预测值 + A的残差 = A的实际值），所以A的残差就是16-15=1（注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值）。进而得到A,B,C,D的残差分别为-1,1，-1,1。然后我们拿残差替代A,B,C,D的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。

换句话说，现在A,B,C,D的预测值都和真实年龄一致了。Perfect!：

A: 14岁高一学生，购物较少，经常问学长问题；预测年龄A = 15 – 1 = 14

B: 16岁高三学生；购物较少，经常被学弟问问题；预测年龄B = 15 + 1 = 16

C: 24岁应届毕业生；购物较多，经常问师兄问题；预测年龄C = 25 – 1 = 24

D: 26岁工作两年员工；购物较多，经常被师弟问问题；预测年龄D = 25 + 1 = 26

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------

看完例子，想必大家已经基本了解GBDT的原理了，那我们下面看梯度提升法在不同损失函数用法

把梯度提升法的思想带入逻辑回归损失函数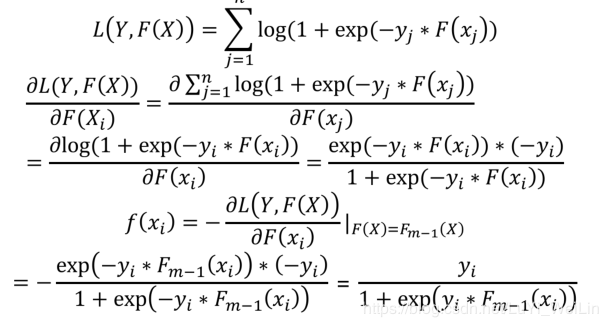

把梯度提升法的思想带入分类类型的损失函数

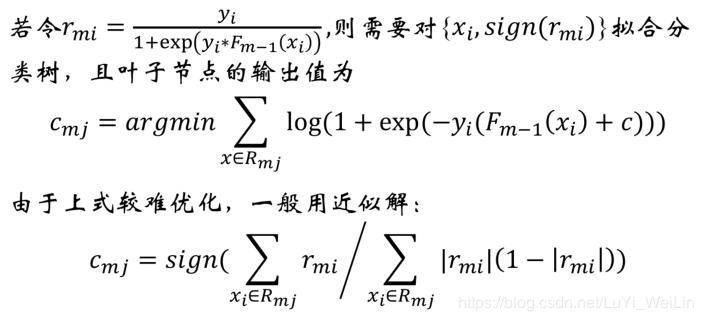
GBDT模型如何调整参数

GBDT该调整哪些参数

一般集成模型的参数分为两种类别：

• 框架层面参数
• 基模型层面参数

当然啦，GBDT模型框架层面参数和基模型层面参数是有非常多参数的，经验得出我们只需要关注以下几个变量即可（当然，特殊情况特殊处理）

• 框架层面参数

基模型层面参数

如何进行参数调节

我们使用到的方法是：K折交叉验证（CV）

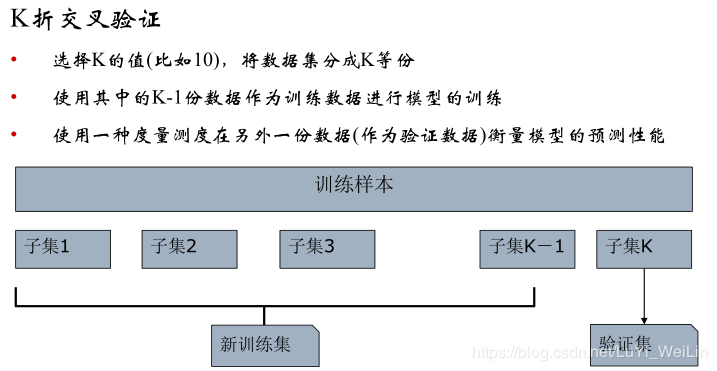
其优缺点：

基于k折交叉验证的网格搜索法（GridSearchCV）

每变一个参数，模型都要拟合一遍，大样本就会很卡。使用贪心算法，把n1*n2*n3*n4*......*nk复杂度变为n1+n2+n3+n4+......+nk，求其次优解。按照变量（框架层面参数、基模型层面参数）的重要程度来顺序调参。

GBDT模型对样本违约概率进行估计
代码请看下一篇博客

GBDT模型挑选变量重要性
集成模型几乎都能给出变量重要性的估计，因为有抽样成分在里面

GBDT模型如何进行变量的衍生
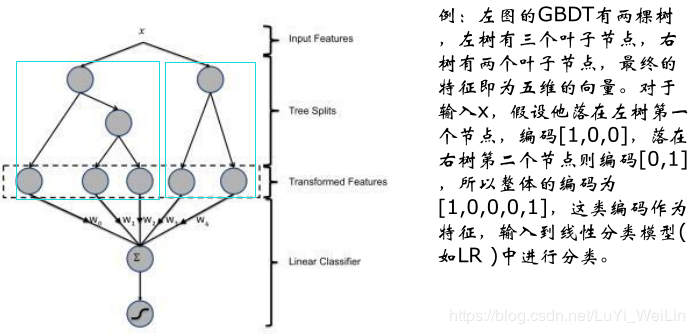
独热编码
在讲解变量衍生之前我们来了解一下独热编码（引用一下别人的博客介绍一下独热编码）

----------------------------------------------------------------------------------------------

原文：https://blog.csdn.net/windowsyun/article/details/78277880

简单介绍
有一组数据，其中有个特征是性别。既然是性别，那它的值显然只有两个选择，要么男性（用1表示）要么女性（用0表示）。 
独热编码就是将这一个特征变成两个特征：是男性、是女性。 
我是男的，我的特征就变成了 [1, 0]，1代表我是男的，0代表我不是女的。同样，女性的特征变为[0, 1]。

用处
为什么用独热编码？ 
假设一个特征是颜色，选项有：黄色、红色、绿色等等。如果我们不采用独热编码，用0表示黄色，用1表示绿色，用2表示红色，以此类推。从数学上看，它们之间的距离不一样了，0和1的距离显然比0和2的距离小，可是不能认为黄色与红色的关系比绿色更接近。 
采用独热编码后，黄色变成[1, 0, 0 , … ]，红色变成[0, 1, 0, … ]，绿色变成[0, 0, 1, … ]，这样它们的相似度就一样了，这对机器学习算法很重要。

独热编码注意事项

python代码如下

import pandas as pd
import time
import numpy as np
import re
from sklearn.ensemble import GradientBoostingClassifier
from sklearn import cross_validation, metrics
from sklearn.model_selection import GridSearchCV, train_test_split
import matplotlib.pylab as plt
import datetime
from dateutil.relativedelta import relativedelta
from numpy import log
from sklearn.metrics import roc_auc_score
from sklearn.feature_extraction import DictVectorizer
from sklearn.preprocessing import OneHotEncoder
from sklearn.linear_model.logistic import LogisticRegression

def CareerYear(x):
    #对工作年限进行转换
    if str(x).find('nan') > -1:
        return -1
    elif str(x).find("10+")>-1:   #将"10＋years"转换成 11
        return 11
    elif str(x).find('< 1') > -1:  #将"< 1 year"转换成 0
        return 0
    else:
        return int(re.sub("\D", "", x))   #其余数据，去掉"years"并转换成整数

def DescExisting(x):
    #将desc变量转换成有记录和无记录两种
    if type(x).__name__ == 'float':
        return 'no desc'
    else:
        return 'desc'

def ConvertDateStr(x):
    mth_dict = {'Jan': 1, 'Feb': 2, 'Mar': 3, 'Apr': 4, 'May': 5, 'Jun': 6, 'Jul': 7, 'Aug': 8, 'Sep': 9, 'Oct': 10,
                'Nov': 11, 'Dec': 12}
    if str(x) == 'nan':
        return datetime.datetime.fromtimestamp(time.mktime(time.strptime('9900-1','%Y-%m')))
        #time.mktime 不能读取1970年之前的日期
    else:
        yr = int(x[4:6])
        if yr <=17:
            yr = 2000+yr
        else:
            yr = 1900 + yr
        mth = mth_dict[x[:3]]
        return datetime.datetime(yr,mth,1)

def MonthGap(earlyDate, lateDate):
    if lateDate > earlyDate:
        gap = relativedelta(lateDate,earlyDate)
        yr = gap.years
        mth = gap.months
        return yr*12+mth
    else:
        return 0

def MakeupMissing(x):
    if np.isnan(x):
        return -1
    else:
        return x

'''
第一步：数据准备
'''
folderOfData = foldOfData = 'H:/'
allData = pd.read_csv(folderOfData + '数据集.csv',header = 0, encoding = 'latin1',engine ='python')
allData['term'] = allData['term'].apply(lambda x: int(x.replace(' months','')))
# 处理标签：Fully Paid是正常用户；Charged Off是违约用户
allData['y'] = allData['loan_status'].map(lambda x: int(x == 'Charged Off'))

'''
由于存在不同的贷款期限（term），申请评分卡模型评估的违约概率必须要在统一的期限中，且不宜太长，所以选取term＝36months的行本
'''
allData1 = allData.loc[allData.term == 36]
trainData, testData = train_test_split(allData1,test_size=0.4)

'''
第二步：数据预处理
'''
# 将带％的百分比变为浮点数
trainData['int_rate_clean'] = trainData['int_rate'].map(lambda x: float(x.replace('%',''))/100)
# 将工作年限进行转化，否则影响排序
trainData['emp_length_clean'] = trainData['emp_length'].map(CareerYear)
# 将desc的缺失作为一种状态，非缺失作为另一种状态
trainData['desc_clean'] = trainData['desc'].map(DescExisting)
# 处理日期。earliest_cr_line的格式不统一，需要统一格式且转换成python的日期
trainData['app_date_clean'] = trainData['issue_d'].map(lambda x: ConvertDateStr(x))
trainData['earliest_cr_line_clean'] = trainData['earliest_cr_line'].map(lambda x: ConvertDateStr(x))
# 处理mths_since_last_delinq。注意原始值中有0，所以用－1代替缺失
trainData['mths_since_last_delinq_clean'] = trainData['mths_since_last_delinq'].map(lambda x:MakeupMissing(x))
trainData['mths_since_last_record_clean'] = trainData['mths_since_last_record'].map(lambda x:MakeupMissing(x))
trainData['pub_rec_bankruptcies_clean'] = trainData['pub_rec_bankruptcies'].map(lambda x:MakeupMissing(x))

'''
第三步：变量衍生
'''
# 考虑申请额度与收入的占比
trainData['limit_income'] = trainData.apply(lambda x: x.loan_amnt / x.annual_inc, axis = 1)
# 考虑earliest_cr_line到申请日期的跨度，以月份记
trainData['earliest_cr_to_app'] = trainData.apply(lambda x: MonthGap(x.earliest_cr_line_clean,x.app_date_clean), axis = 1)

'''
对于类别型变量，需要onehot（独热）编码，再训练GBDT模型
'''
num_features = ['int_rate_clean','emp_length_clean','annual_inc', 'dti', 'delinq_2yrs', 'earliest_cr_to_app','inq_last_6mths', \
                'mths_since_last_record_clean', 'mths_since_last_delinq_clean','open_acc','pub_rec','total_acc','limit_income','earliest_cr_to_app']
cat_features = ['home_ownership', 'verification_status','desc_clean', 'purpose', 'zip_code','addr_state','pub_rec_bankruptcies_clean']

#独热编码
v = DictVectorizer(sparse=False)
X1 = v.fit_transform(trainData[cat_features].to_dict('records'))
#将独热编码和数值型变量放在一起进行模型训练
X2 = np.matrix(trainData[num_features])
X = np.hstack([X1,X2])
y = trainData['y']

# 未经调参进行GBDT模型训练
gbm0 = GradientBoostingClassifier(random_state=10)
gbm0.fit(X,y)

y_pred = gbm0.predict(X)
y_predprob = gbm0.predict_proba(X)[:,1].T
print("Accuracy : %.4g" % metrics.accuracy_score(y, y_pred))
print("AUC Score (Train): %f" % metrics.roc_auc_score(np.array(y.T), y_predprob))

'''
第四步：在测试集上测试模型的性能
'''
# 将带％的百分比变为浮点数
testData['int_rate_clean'] = testData['int_rate'].map(lambda x: float(x.replace('%',''))/100)
# 将工作年限进行转化，否则影响排序
testData['emp_length_clean'] = testData['emp_length'].map(CareerYear)
# 将desc的缺失作为一种状态，非缺失作为另一种状态
testData['desc_clean'] = testData['desc'].map(DescExisting)
# 处理日期。earliest_cr_line的格式不统一，需要统一格式且转换成python的日期
testData['app_date_clean'] = testData['issue_d'].map(lambda x: ConvertDateStr(x))
testData['earliest_cr_line_clean'] = testData['earliest_cr_line'].map(lambda x: ConvertDateStr(x))
# 处理mths_since_last_delinq。注意原始值中有0，所以用－1代替缺失
testData['mths_since_last_delinq_clean'] = testData['mths_since_last_delinq'].map(lambda x:MakeupMissing(x))
testData['mths_since_last_record_clean'] = testData['mths_since_last_record'].map(lambda x:MakeupMissing(x))
testData['pub_rec_bankruptcies_clean'] = testData['pub_rec_bankruptcies'].map(lambda x:MakeupMissing(x))

# 考虑申请额度与收入的占比
testData['limit_income'] = testData.apply(lambda x: x.loan_amnt / x.annual_inc, axis = 1)
# 考虑earliest_cr_line到申请日期的跨度，以月份记
testData['earliest_cr_to_app'] = testData.apply(lambda x: MonthGap(x.earliest_cr_line_clean,x.app_date_clean), axis = 1)

#用训练集里的onehot编码方式进行编码
X1_test = v.transform(testData[cat_features].to_dict('records'))
X2_test = np.matrix(testData[num_features])
X_test = np.hstack([X1_test,X2_test])
y_test = np.matrix(testData['y']).T

### 计算KS值
def KS(df, score, target):
    '''
    :param df: 包含目标变量与预测值的数据集,dataframe
    :param score: 得分或者概率,str
    :param target: 目标变量,str
    :return: KS值
    '''
    total = df.groupby([score])[target].count()
    bad = df.groupby([score])[target].sum()
    all = pd.DataFrame({'total':total, 'bad':bad})
    all['good'] = all['total'] - all['bad']
    all[score] = all.index
    all = all.sort_values(by=score,ascending=False)
    all.index = range(len(all))
    all['badCumRate'] = all['bad'].cumsum() / all['bad'].sum()
    all['goodCumRate'] = all['good'].cumsum() / all['good'].sum()
    KS = all.apply(lambda x: x.badCumRate - x.goodCumRate, axis=1)
    return max(KS)

#在测试集上测试GBDT性能
y_pred = gbm0.predict(X_test)
y_predprob = gbm0.predict_proba(X_test)[:,1].T
testData['predprob'] = list(y_predprob)
print("Accuracy : %.4g" % metrics.accuracy_score(y_test, y_pred))
print("AUC Score (Test): %f" % metrics.roc_auc_score(np.array(y_test)[:,0], y_predprob))
print("KS is :%f" % KS(testData, 'predprob', 'y'))

'''
GBDT调参
'''
# 1, 选择较小的步长(learning rate)后，对迭代次数(n_estimators)进行调参

X = pd.DataFrame(X)

param_test1 = {'n_estimators':range(80,81,10)}
gsearch1 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, min_samples_split=30,min_samples_leaf=5,max_depth=8,max_features='sqrt', subsample=0.8,random_state=10),param_grid = param_test1, scoring='roc_auc',iid=False,cv=5)
gsearch1.fit(X,y)
gsearch1.best_params_, gsearch1.best_score_
best_n_estimator = gsearch1.best_params_['n_estimators']

# 2, 对决策树最大深度max_depth和内部节点再划分所需最小样本数min_samples_split进行网格搜索
param_test2 = {'max_depth':range(3,4), 'min_samples_split':range(6,7)}
gsearch2 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=best_n_estimator, min_samples_leaf=20, max_features='sqrt', subsample=0.8, random_state=10),param_grid = param_test2, scoring='roc_auc',iid=False, cv=5)
gsearch2.fit(X,y)
gsearch2.best_params_, gsearch2.best_score_
best_max_depth = gsearch2.best_params_['max_depth']

#3, 再对内部节点再划分所需最小样本数min_samples_split和叶子节点最少样本数min_samples_leaf一起调参
param_test3 = {'min_samples_split':range(80,81,10), 'min_samples_leaf':range(50,51,5)}
gsearch3 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=best_n_estimator,max_depth=best_max_depth,max_features='sqrt', subsample=0.8, random_state=10),param_grid = param_test3, scoring='roc_auc',iid=False, cv=5)
gsearch3.fit(X,y)
gsearch3.best_params_, gsearch3.best_score_
best_min_samples_split, best_min_samples_leaf = gsearch3.best_params_['min_samples_split'],gsearch3.best_params_['min_samples_leaf']

#4, 对最大特征数max_features进行网格搜索
param_test4 = {'max_features':range(int(np.sqrt(X.shape[0])),int(np.sqrt(X.shape[0]))+1,5)}
gsearch4 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=best_n_estimator,max_depth=best_max_depth, min_samples_leaf =best_min_samples_leaf,min_samples_split =best_min_samples_split, subsample=0.8, random_state=10),param_grid = param_test4, scoring='roc_auc',iid=False, cv=5)
gsearch4.fit(X,y)
gsearch4.best_params_, gsearch4.best_score_
best_max_features = gsearch4.best_params_['max_features']

#5, 对采样比例进行网格搜索
param_test5 = {'subsample':[0.6+i*0.05 for i in range(1)]}
gsearch5 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=best_n_estimator,max_depth=best_max_depth,min_samples_leaf =best_min_samples_leaf, max_features=best_max_features,random_state=10),param_grid = param_test5, scoring='roc_auc',iid=False, cv=5)
gsearch5.fit(X,y)
gsearch5.best_params_, gsearch5.best_score_
best_subsample = gsearch5.best_params_['subsample']

gbm_best = GradientBoostingClassifier(learning_rate=0.1, n_estimators=best_n_estimator,max_depth=best_max_depth,min_samples_leaf =best_min_samples_leaf, max_features=best_max_features,subsample =best_subsample, random_state=10)
gbm_best.fit(X,y)

#在测试集上测试并计算性能
y_pred = gbm_best.predict(X_test)
y_predprob = gbm_best.predict_proba(X_test)[:,1].T
testData['predprob'] = list(y_predprob)
#准确性
print("Accuracy : %.4g" % metrics.accuracy_score(y_test, y_pred))
print("AUC Score (Test): %f" % metrics.roc_auc_score(np.array(y_test)[:,0], y_predprob))
print("KS is :%f"%KS(testData, 'predprob', 'y'))

###########概率转换为分数########################
def Prob2Score(prob, basePoint, PDO):
    #将概率转化成分数且为正整数
    y = np.log(prob/(1-prob))
    return int(basePoint+PDO/np.log(2)*(-y))

basePoint = 250
PDO = 50
testData['score'] = testData['predprob'].map(lambda x:Prob2Score(x, basePoint, PDO))
testData = testData.sort_values(by = 'score')
#画出分布图
plt.hist(testData['score'], 100)
plt.xlabel('score')
plt.ylabel('freq')
plt.title('distribution')

　　

python风控建模实战lendingClub(博主录制，catboost，lightgbm建模，2K超清分辨率)

https://study.163.com/course/courseMain.htm?courseId=1005988013&share=2&shareId=400000000398149

微信扫二维码，免费学习更多python资源