Dijkstra算法(朴素实现、优先队列优化)

Dijkstra算法只能求取边的权重为非负的图的最短路径，而Bellman-Ford算法可以求取边的权重为负的图的最短路径（但Bellman-Ford算法在图中存在负环的情况下，最短路径是不存在的（负无穷））。

算法原理

　　Dijkstra算法本质上是一种贪心算法，1959年，Edsger Dijkstra提出了该算法用于解决单源最短路径问题，即在给定每条边的长度\(\mathcal{l}\)，求取源节点s到其它所有节点的最短路径。Dijkstra算法维护一个节点集合S，S中的节点到源点的最短距离d已经确定了，即“Explored”。

　　初始化时，\(S={s},d(s)=0\)，接下来开始循环，对于每一个节点\(v\in V-S\)，选出到集合S的距离最近的节点\(v^*\)，即最小化下面这个问题：

\begin{equation}

d'(v)=\min_{e=(u,v):u\in S}d(u)+\mathcal{l}_e

\end{equation}

我们将\(v^*\)加入到集合S，并定义\(d(v^*)=d'(v^*)\)。然后继续下一次循环。

　　算法伪代码如下：

图1 Dijkstra算法伪代码

复杂度分析

朴素实现

　　每次while循环，将1个节点加入集合S中，所以共n-1次外层循环。对于一个有m条边的图而言，求解式(1)最坏情况下，需要遍历所有的边，即需要\(\mathcal{O}(m)\)的时间复杂度，所以程序整体的时间复杂度为\(\mathcal{O}(mn)\)。如果看下文例题中POJ2387的朴素实现，可能会发现算法复杂度是\(\mathcal{O}(n^2)\)，不是\(\mathcal{O}(mn)\)。但其实在例题中，在输入时，每两个节点间只有一条边相连（如果有多条，则只保留最短的一条），另外，每次将节点v_opt新加入S中时，我们会更新v_opt节点相邻的节点的\(d'(v)\)的值，并将其存储在数组中。从而每次求解式(1)时，我们只需要遍历非S集合的节点的\(d'(v)\)值，就能得到式(1)的答案，从而降低了求解式(1)的复杂度（降为\(\mathcal{O}(n)\)），整体复杂度降为\(\mathcal{O}(n^2)\)，而对于一般情况，理论上的复杂度就是\(\mathcal{O}(mn)\)。

优先队列优化

　　上文中提到将非S集合的节点的\(d'(v)\)值存储在数组里，每次遍历数组得到式(1)的答案（即\(d'(v)\)的最小值），而这一个地方还可以进一步优化，采取优先队列存储非S集合的节点，节点对应的\(d'(v)\)作为键值，若采用二叉堆实现优先队列（可以参考优先队列及（二叉）堆），每次只需要\(\mathcal{O}(\log n)\)的时间即可求得\(d'(v)\)的最小值（得到最小值后需删除该值）。

　　优先队列实现的伪代码如下：

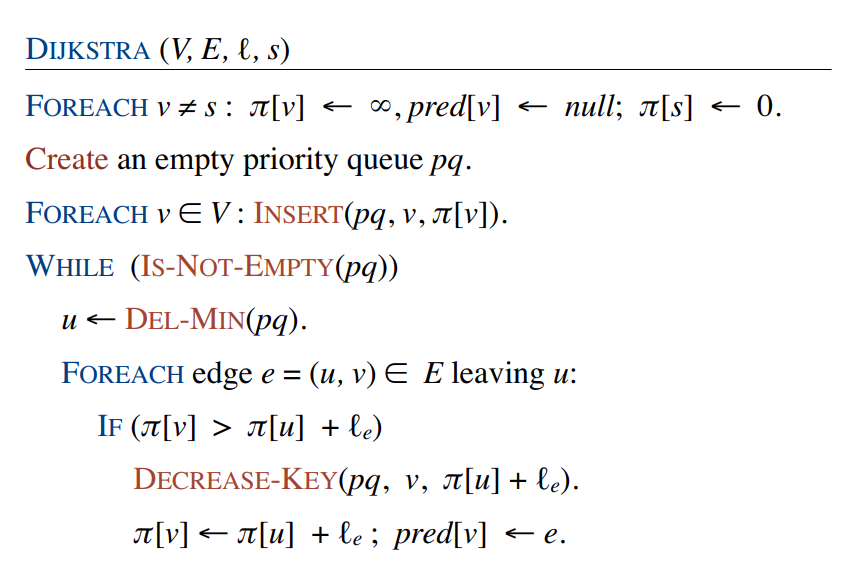
图2 Dijkstra优先队列实现算法伪代码
　　若图有n个节点，m条边($m\ge n$)，该算法对每个节点调用一个INSERT操作和DEL-MIN操作。for循环总共有m次，调用DECREASE-KEY最多有m次，而每次INSERT、DEL-MIN、DECREASE-KEY操作的时间都是$\mathcal{O}(\log n)$，则总体而言时间为$\mathcal{O}((n+m)\log n)$。对于稀疏图而言，即若$m=o(n^2/\log n)$$^{[2]}$，总体时间为$\mathcal{O}(m\log n)$，较朴素实现是有明显改善的。

例题

POJ2387

　　典型Dijkstra模板题，需要注意不同landmark(节点)间的路径可能有多条，这是一个WA点，若用邻接矩阵存储图，解决办法是只保留最短的一条路径。若用邻接表存储图，则不需要对重复边进行特别处理。

朴素实现

　　用explored数组来标记是否属于集合S，外层for循环共执行n次，每次标记一个节点，循环内遍历非S集合的节点，求出到S集合的距离最短的节点v_opt，然后更新与v_opt相邻的节点\(d'(v)\)（即distance数组）的值。整体复杂度\(\mathcal{O}(n^2)\)

Result: 4280kB, 125ms. 说起来POJ的Time不是很固定啊，同样的代码，上次是63ms，这次是125ms。

#include <stdio.h>
#include <string.h>
#include <limits.h>
#include <queue>
int t, n;
int adjacency_matrix[1005][1005];
int distance[1005];
int explored[1005];//标记是否属于集合S
void DijkstraSimple() {
	distance[n] = 0;
	for (int i = 1; i <= n; i++) {//每次将一个节点加入S，共循环n次
		int min = 0x3f3f3f3f;
		int v_opt;//最小化式(1)的节点
		for (int v = 1; v <= n; v++)//找出S集合中最小化式(1)的节点
			if (!explored[v] && distance[v] < min) {
				min = distance[v];
				v_opt = v;
			}
		explored[v_opt] = 1;
		for (int v = 1; v <= n; v++)
			if (!explored[v])//v未添加进集合S且v_opt、v之间有边相连
				distance[v] = std::min(distance[v], distance[v_opt] + adjacency_matrix[v_opt][v]);
	}
}
int main() {
	while (scanf("%d %d", &t, &n) != EOF) {
		memset(adjacency_matrix, 0x3f, sizeof(adjacency_matrix));
		memset(distance, 0x3f, sizeof(distance));
		memset(explored, 0, sizeof(explored));
		int u, v, length;
		for (int i = 1; i <= t; i++) {
			scanf("%d %d %d", &u, &v, &length);
			if (adjacency_matrix[u][v] > length) {//两个landmark之间可能有多条路，这是一个WA点，有多条路时，取length最小的路
			adjacency_matrix[u][v] = length;
			adjacency_matrix[v][u] = length;
			}
		}
		DijkstraSimple();
		printf("%d\n", distance[1]);
	}
	return 0;
}

优先队列实现

　　图2优先队列实现的伪代码中，要求通过decrease_key函数改变特定节点\(v\)的键值，但实际上，正如我的优先队列及（二叉）堆这篇博客中提到的，优先队列的基本操作并不包含改变特定节点的键值。在优先队列及（二叉）堆库函数实现小节中，我也提到可以通过维护一个position数组来实现改变特定节点的键值。下列代码正是基于这种思路实现改变特定节点的键值。

　　Result: 388kB, 16ms; 388kB, 32ms. POJ的Time确实不太稳定，同样的代码，隔十分钟提交的结果就不太一样。但是相对朴素实现速度提高很多。

/*
	自己实现的堆算法，通过position记录下元素在堆（数组）中的位置，可以直接更改特定编号的元素的键值
*/
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <algorithm>
//上限
#define N (1000 + 10)
#define M (4000 + 10)//无向图，应大于边数量的2倍
#define parent(i) (int)floor(i/2)
#define left(i) i * 2
#define right(i) i * 2 + 1
struct element {
	int number;//元素编号
	int key;//元素键值
	element() {}
	element(int number, int key) : number(number), key(key) {}
};
element A[N];//存储最小堆
int position[N];//存储元素在堆(数组)中的位置
int min_heap_size;
int explored[N];//标记是否属于集合S
int distance[N];//距源点的最短距离
int t, n;
struct edge {//通过链表存储边
	int v, length, next;
};
edge e[M];
int head[N];//节点的第一条边在e数组中位置
int num_of_edges;
int add_edge(int u, int v, int length1, int length2) {
	int& i = num_of_edges;
	e[i].v = v;
	e[i].length = length1;
	e[i].next = head[u];
	head[u] = i++;
	e[i].v = u;
	e[i].length = length2;
	e[i].next = head[v];
	head[v] = i++;
	return i;
}
template<class T> void exchange(element* array, int i, int j) {
	position[A[i].number] = j;//交换两者的位置
	position[A[j].number] = i;
	T temp = array[i];//交换二者的数据
	array[i] = array[j];
	array[j] = temp;
}
//最小堆
void heap_decrease_key(int i, int key) {
	if (key > A[i].key)
		printf("error: new key is bigger than current key.");
	A[i].key = key;
	while (i > 1 && A[parent(i)].key > A[i].key)
	{
		exchange<element>(A, i, parent(i));
		i = parent(i);
	}
}
void min_heap_insert(element elem) {
	min_heap_size++;
	A[min_heap_size].number = elem.number;
	A[min_heap_size].key = 0x3f3f3f3f;
	position[elem.number] = min_heap_size;//记录下位置
	heap_decrease_key(min_heap_size, elem.key);
}
element heap_minimum() {
	return A[1];
}
void min_heapify(int i) {
	int l = left(i), r = right(i);
	int smallest = i;
	if (l <= min_heap_size && A[l].key < A[i].key)
		smallest = l;
	if (r <= min_heap_size && A[r].key < A[smallest].key)
		smallest = r;
	if (smallest != i) {
		exchange<element>(A, i, smallest);
		min_heapify(smallest);
	}
}
element heap_extract_min(void) {
	element min = A[1];
	position[A[min_heap_size].number] = 1;//heap_size位置的挪到1的位置
	A[1] = A[min_heap_size];
	min_heap_size--;
	min_heapify(1);
	return min;
}
void DijkstraPriorityQueue() {
	min_heap_insert(element(n, 0));
	distance[n] = 0;
	for (int i = 1; i < n; i++)//将所有节点都放入优先队列中
		min_heap_insert(element(i, 0x3f3f3f3f));
	for (int i = 1; i <= n; i++) {//每次把一个节点从优先队列中取出加入到S中，外层循环n次
		element front_elem = heap_extract_min();
		int u = front_elem.number;
		explored[u] = 1;
		distance[u] = front_elem.key;
		for (int j = head[u]; j >= 0; j = e[j].next) {//遍历u出发的所有边
			int v = e[j].v;
			if (explored[v])
				continue;
			if (A[position[v]].key > distance[u] + e[j].length)
				heap_decrease_key(position[v], distance[u] + e[j].length);
		}
	}
}
void Init() {
	min_heap_size = 0;
	memset(position, -1, sizeof(position));
	memset(explored, 0, sizeof(explored));
	memset(distance, 0x3f, sizeof(distance));
	num_of_edges = 0;
	memset(head, -1, sizeof(head));
}
int main() {
	while (scanf("%d %d", &t, &n) != EOF){
		Init();
		int u, v, length;
		for (int i = 1; i <= t; i++) {
			scanf("%d %d %d", &u, &v, &length);
			add_edge(u, v, length, length);
		}
		DijkstraPriorityQueue();
		printf("%d\n", distance[1]);
	}
	return 0;
}

参考：

[1] 算法设计

[2] 算法导论