二叉树&满二叉树与完全二叉树

二叉树的定义

二叉树（Binary Tree）是n（n≥0）个元素的有限集合，该集合为空或者为由一个称为“根”的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成
二叉树的基本特点：

每个结点最多有两棵子树

左子树和右子树是有顺序的，且不可颠倒

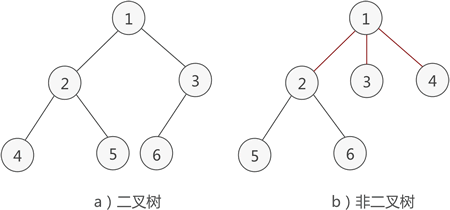
图一

节点、度和叶子的概念

1、结点

二叉树中的每一个元素都称为结点。通常二叉树的许多名词借用了家族关系
例如在上图中，2、3均是1的子结点，1是2&3的双亲，因而2、3互为“兄弟结点”

2、度

二叉树的度代表某个结点的孩子或者后继人的个数，1度表示只有一个孩子或者称之为单子树，2度是两个孩子或者说左右子树都有的二叉树。当然，二叉树某个结点的最大度为2.例如2的度数为2，3的度数为1

叶子

叶子是叶子结点的简称，叶子也就是leaf，原指网络结构中的某些计算机，它们从比较靠近中心的计算机处接收信号，而不把信号传至较远的计算机。在二叉树中叶子结点指树种处于最底端的结点，叶子结点没有子结点 例如上图中的 4、5、6均为叶子结点

特殊二叉树

图二

特殊二叉树有：满二叉树和完全二叉树

满二叉树：

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的一棵二叉树称之为满二叉树
例如图二中的第一张图，即为一棵满二叉树。而第二张图的B结点由于没有右子节树，所以不是满二叉树。
满二叉树的特点有：

1.叶子只能出现在最下一层
2.非叶子结点的度一定为2
3.在同样深度的二叉树中，满二叉树的结点个数最多，叶子最多

完全二叉树

一棵深度为k的有n个结点的二叉树，从树中的结点按从上至下、从左至右的顺序进行编号，如果编号为i（1≤i≤n）的节点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树，如图二的第三张图。

1.叶子结点只能出现在最下两层
2.最下层的叶子若有结点，一定集中在左下部分
3.倒数第二层若有叶子结点，一定都集中在右半部分
4.如果结点度为1，则该结点只有左孩子，即不存在只有右孩子之说。
5.同样结点数的二叉树，完全二叉树的深度最小