洛谷 P3371 【模板】单源最短路径（弱化版） 题解

P3371 【模板】单源最短路径（弱化版）

题目背景

本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过，如有需要请移步 P4779。

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入格式

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入 #1

4 6 1

1 2 2

2 3 2

2 4 1

1 3 5

3 4 3

1 4 4

输出 #1

0 2 4 3

说明/提示

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15；

对于40%的数据：N<=100，M<=10000；

对于70%的数据：N<=1000，M<=100000；

对于100%的数据：N<=10000，M<=500000。保证数据随机。

对于真正 100% 的数据，请移步 P4779。请注意，该题与本题数据范围略有不同。

样例说明：

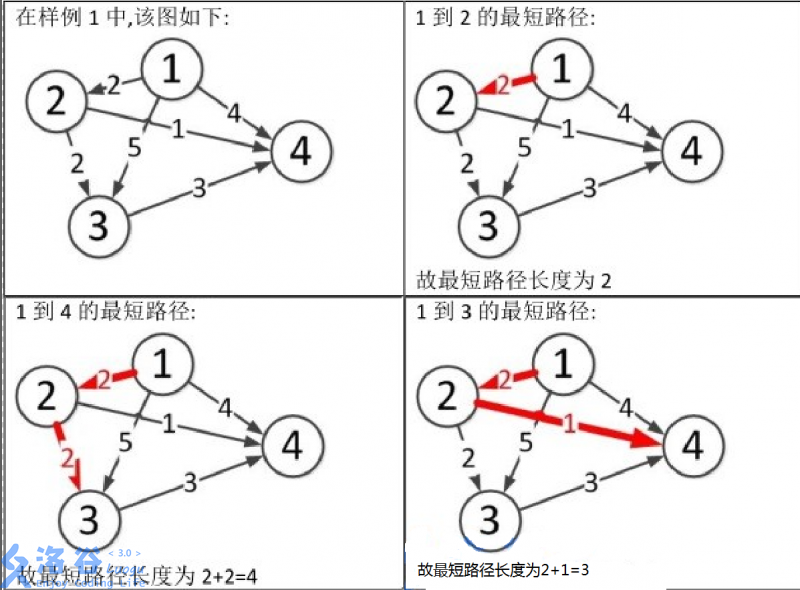
图片1到3和1到4的文字位置调换

【思路or瞎bb】

跑SPFA就好了

没有可以卡SPFA

起码SPFA在这道题目上面诈尸了一下下

【完整代码】

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int Max = 10000005;
const int M = 10005;
struct node
{
	int y,ne;
	int z;
}a[Max];//结构体储存邻接链表
int sum = 0;
int n,m,s;
int head[M];

void add(int x,int y,int z)//插入邻接链表
{
	a[++ sum].y = y;
	a[sum].ne = head[x];
	a[sum].z = z;
	head[x] = sum;
}

int d[M];//起点到某个点的距离
bool use[M];//判断有没有出现过 

void SPFA()
{
	queue<int> q;
	q.push(s);
	for(register int i = 1;i <= n;++ i)
		d[i] = 99999999;//赋值一个很大的数但是不能够赋值为0x7fffffff因为后面还有加法，如果两个0x7fffffff或者一个和另一个别的数相加就会爆炸int
	d[s] = 0;//自己到自己的距离为0
	while(!q.empty())
	{
		int qwq = q.front();
		q.pop();use[qwq] = false;//已经出队，下一次可以入队
		for(register int i = head[qwq];i != 0;i = a[i].ne)
		{
			int awa = a[i].y;
			if(d[awa] > d[qwq] + a[i].z)
			{
				d[awa] = d[qwq] + a[i].z;
				if(use[awa] == false)
				{
					use[awa] = true;
					q.push(awa);
				}
			}
		}
	}
}

int main()
{
	scanf("%d%d%d",&n,&m,&s);
	int x,y,z;
	for(register int i = 1;i <= m;++ i)
	{
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
	}
	SPFA();
	for(register int i = 1;i <= n;++ i)
	{
		if(d[i] != 99999999)//因为前面不能赋值0x7fffffff但是输出的时候还需要输出0x7fffffff所以特判一下
			cout << d[i] << " ";
		else
			cout << 0x7fffffff << " ";
	}
	return 0;
}